Complexity: A Guided Tour - Melanie Mitchell (2009)
Part IV. Network Thinking
Chapter 16. Applying Network Science to Real-World Networks
NETWORK THINKING IS EVIDENTLY ON a lot of people’s minds. According to my search on the Google Scholar Web site, at the time of this writing over 14,000 academic papers on small-world or scale-free networks have been published in the last five years (since 2003), nearly 3,000 in the last year alone. I did a scan of the first 100 or so titles in the list and found that 11 different disciplines are represented, ranging from physics and computer science to geology and neuroscience. I’m sure that the range of disciplines I found would grow substantially if I did a more comprehensive scan.
In this chapter I survey some diverse examples of real-world networks and discuss how advances in network science are influencing the way scientists think about networks in many disciplines.
Examples of Real-World Networks
THE BRAIN
Several groups have found evidence that the brain has small-world properties. The brain can be viewed as a network at several different levels of description; for example, with neurons as nodes and synapses as links, or with entire functional areas as nodes and larger-scale connections between them (i.e., groups of neural connections) as links.
As I mentioned in the previous chapter, the neurons and neural connections of the brain of the worm C. elegans have been completely mapped by neuroscientists and have been shown to form a small-world network. More recently, neuroscientists have mapped the connectivity structure in certain higher-level functional brain areas in animals such as cats, macaque monkeys, and even humans and have found the small-world property in those structures as well.
Why would evolution favor brain networks with the small-world property? Resilience might be one major reason: we know that individual neurons die all the time, but, happily, the brain continues to function as normal. The hubsof the brain are a different story: if a stroke or some other mishap or disease affects, say, the hippocampus (which is a hub for networks encoding short-term memory), the failure can be quite devastating.
In addition, researchers have hypothesized that a scale-free degree distribution allows an optimal compromise between two modes of brain 'margin-bottom:0cm;margin-bottom:.0001pt;text-align: justify;text-indent:12.0pt;line-height:normal'>If every neuron were connected to every other neuron, or all different functional areas were fully connected to one another, then the brain would use up a mammoth amount of energy in sending signals over the huge number of connections. Evolution presumably selected more energy-efficient structures. In addition, the brain would probably have to be much larger to fit all those connections. At the other extreme, if there were no long-distance links in the brain, it would take too long for the different areas to communicate with one another. The human brain size—and corresponding skull size—seems to be exquisitely balanced between being large enough for efficient complex cognition and small enough for mothers to give birth. It has been proposed that the small-world property is exactly what allows this balance.
It has also been widely speculated that synchronization, in which groups of neurons repeatedly fire simultaneously, is a major mechanism by which information in the brain is communicated efficiently, and it turns out that a small-world connectivity structure greatly facilitates such synchronization.
GENETIC REGULATORY NETWORKS
As I mentioned in chapter 7, humans have about 25,000 genes, roughly the same number as the mustard plant arabidopsis. What seems to generate the complexity of humans as compared to, say, plants is not how many genes we have but how those genes are organized into networks.
There are many genes whose function is to regulate other genes—that is, control whether or not the regulated genes are expressed. A well-known simple example of gene regulation is the control of lactose metabolism in E. colibacteria. These bacteria usually live off of glucose, but they can also metabolize lactose. The ability to metabolize lactose requires the cell to contain three particular protein enzymes, each encoded by a separate gene. Let’s call these genes A, B, and C. There is a fourth gene that encodes a protein, called a lactose repressor, which binds to genes A, B, and C, in effect, turning off these genes. If there is no lactose in the bacterium’s local environment, lactose repressors are continually formed, and no lactose metabolism takes place. However, if the bacterium suddenly finds itself in a glucose-free but lactose-rich environment, then lactose molecules bind to the lactose repressor and detach it from genes A, B, and C, which then proceed to produce the enzymes that allow lactose metabolism.
Regulatory interactions like this, some much more intricate, are the heart and soul of complexity in genetics. Network thinking played a role in understanding these interactions as early as the 1960s, with the work of Stuart Kauffman (more on this in chapter 18). More recently, network scientists teaming up with geneticists have demonstrated evidence that at least some networks of these interactions are approximately scale-free. Here, the nodes are individual genes, and each node links to all other genes it regulates (if any).
Resilience is mandatory for genetic regulatory networks. The processes of gene transcription and gene regulation are far from perfect; they are inherently error-ridden and often affected by pathogens such as viruses. Having a scale-free structure helps the system to be mostly impervious to such errors.
Metabolic Networks
As I described in chapter 12, cells in most organisms have hundreds of different metabolic pathways, many interconnecting, forming networks of metabolic reactions. Albert-László Barabási and colleagues looked in detail at the structure of metabolic networks in forty-three different organisms and found that they all were “well fitted” by a power-law distribution—i.e., are scale free. Here the nodes in the network are chemical substrates—the fodder and product of chemical reactions. One substrate is considered to be linked to another if the first participates in a reaction that produces the second. For example, in the second step of the pathway called glycolysis, the substrate glucose-6-phosphate produces the substrate fructose-6-phosphate, so there would be a link in the network from the first substrate to the second.
Since metabolic networks are scale-free, they have a small number of hubs that are the products of a large number of reactions involving many different substrates. These hubs turn out to be largely the same chemicals in all the diverse organisms studied—the chemicals that are known to be most essential for life. It has been hypothesized that metabolic networks evolved to be scale-free so as to ensure robustness of metabolism and to optimize “communication” among different substrates.
Epidemiology
In the early 1980s, in the early stages of the worldwide AIDS epidemic, epidemiologists at the Centers for Disease Control in Atlanta identified a Canadian flight attendant, Gaetan Dugas, as part of a cluster of men with AIDS who were responsible for infecting large numbers of other gay men in many different cities around the world. Dugas was later vilified in the media as “patient zero,” the first North American with AIDS, who was responsible for introducing and widely spreading the AIDS virus in the United States and elsewhere. Although later studies debunked the theory that Dugas was the source of the North American epidemic, there is no question that Dugas, who claimed to have had hundreds of different sexual partners each year, infected many people. In network terms, Dugas was a hub in the network of sexual contacts.
Epidemiologists studying sexually transmitted diseases often look at networks of sexual contacts, in which nodes are people and links represent sexual partnerships between two people. Recently, a group consisting of sociologists and physicists analyzed data from a Swedish survey of sexual behavior and found that the resulting network has a scale-free structure; similar results have been found in studies of other sexual networks.
In this case, the vulnerability of such networks to the removal of hubs can work in our favor. It has been suggested that safe-sex campaigns, vaccinations, and other kinds of interventions should mainly be targeted at such hubs.
How can these hubs be identified without having to map out huge networks of people, for which data on sexual partners may not be available?
A clever yet simple method was proposed by another group of network scientists: choose a set of random people from the at-risk population and ask each to name a partner. Then vaccinate that partner. People with many partners will be more likely to be named, and thus vaccinated, under this scheme.
This strategy, of course, can be exported to other situations in which “hub-targeting” is desired, such as fighting computer viruses transmitted by e-mail: in this case, one should target anti-virus methods to the computers of people with large address books, rather than depending on all computer users to perform virus detection.
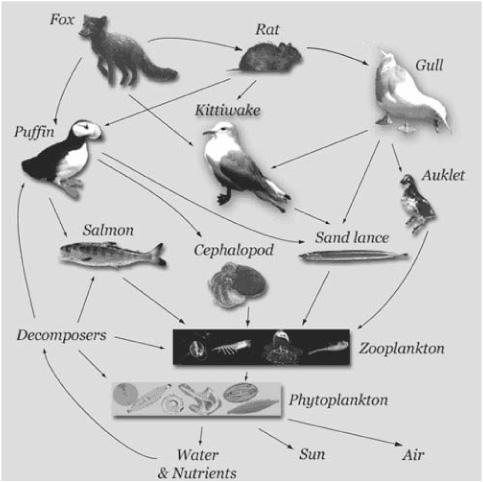
FIGURE 16.1. Example of a food web. (Illustration from USGS Alaska Science Center, [http://www.absc.usgs.gov/research/seabird_foragefish/marinehabitat/home.html].)
Ecologies and Food Webs
In the science of ecology, the common notion of food chain has been extended to food web, a network in which a node represents a species or group of species; if species B is part of the diet of species A, then there is a link from node A to node B. Figure 16.1 shows a simple example of a food web.
Mapping the food webs of various ecosystems has been an important part of ecological science for some time. Recently, researchers have been applying network science to the analysis of these webs in order to understand biodiversity and the implications of different types of disruptions to that biodiversity in ecosystems.
Several ecologists have claimed that (at least some) food webs possess the small-world property, and that some of these have scale-free degree distributions, which evolved presumably to give food webs resilience to the random deletion of species. Others ecologists have disagreed that food webs have scale-free structure, and the ecology research community has recently seen a lot of debate on this issue, mainly due to the difficulty of interpreting real-world data.
Significance of Network Thinking
The examples above are only a small sampling of the ways in which network thinking is affecting various areas of science and technology. Scale-free degree distributions, clustering, and the existence of hubs are the common themes; these features give rise to networks with small-world communication capabilities and resilience to deletion of random nodes. Each of these properties is significant for understanding complex systems, both in science and in technology.
In science, network thinking is providing a novel language for expressing commonalities across complex systems in nature, thus allowing insights from one area to influence other, disparate areas. In a self-referential way, network science itself plays the role of a hub—the common connection among otherwise far-flung scientific disciplines.
In technology, network thinking is providing novel ways to think about difficult problems such as how to do efficient search on the Web, how to control epidemics, how to manage large organizations, how to preserve ecosystems, how to target diseases that affect complex networks in the body, how to target modern criminal and terrorist organizations, and, more generally, what kind of resilience and vulnerabilities are intrinsic to natural, social, and technological networks, and how to exploit and protect such systems.
Where Do Scale-Free Networks Come From?
No one purposely designed the Web to be scale-free. The Web’s degree distribution, like that of the other networks I’ve mentioned above, is an emergent outcome of the way in which the network was formed, and how it grows.
In 1999 physicists Albert-László Barabási and Réka Albert proposed that a particular growing process for networks, which they called preferential attachment, is the explanation for the existence of most (if not all) scale-free networks in the real world. The idea is that networks grow in such a way that nodes with higher degree receive more new links than nodes with lower degree. Intuitively this makes sense. People with many friends tend to meet more new people and thus make more new friends than people with few friends. Web pages with many incoming links are easier to find than those with few incoming links, so more new Web pages link to the high-degree ones. In other words, the rich get richer, or perhaps the linked get more linked. Barabási and Albert showed that growth by preferential attachment leads to scale-free degree distributions. (Unbeknownst to them at the time, this process and its power-law outcome had been discovered independently at least three times before.)
The growth of so-called scientific citation networks is one example of the effects of preferential attachment. Here the nodes are papers in the scientific literature; each paper receives a link from all other papers that cite it. Thus the more citations others have given to your paper, the higher its degree in the network. One might assume that a large number of citations is an indicator of good work; for example, in academia, this measure is routinely used in making decisions about tenure, pay increases, and other rewards. However, it seems that preferential attachment often plays a large role. Suppose you and Joe Scientist have independently written excellent articles about the same topic. If I happen to cite your article but not Joe’s in my latest opus, then others who read only my paper will be more likely to cite yours (usually without reading it). Other people will read their papers, and also be more likely to cite you than to cite Joe. The situation for Joe gets worse and worse as your situation gets better and better, even though your paper and Joe’s were both of the same quality. Preferential attachment is one mechanism for getting to what the writer Malcolm Gladwell called tipping points—points at which some process, such as citation, spread of fads, and so on, starts increasing dramatically in a positive-feedback cycle. Alternatively, tipping points can refer to failures in a system that induce an accelerating systemwide spread of additional failures, which I discuss below.
Power Laws and Their Skeptics
So far I have implied that scale-free networks are ubiquitous in nature due to the adaptive properties of robustness and fast communication associated with power-law degree distributions, and that the mechanism by which they form is growth by preferential attachment. These notions have given scientists new ways of thinking about many different scientific problems.
However compelling all this may seem, scientists are supposed to be skeptical by nature, especially of new, relatively untested ideas, and even more particularly of ideas that claim generality over many disciplines. Such skepticism is not only healthy, it is also essential for the progress of science. Thus, fortunately, not everyone has jumped on the network-science bandwagon, and even many who have are skeptical concerning some of the most optimistic statements about the significance of network science for complex systems research. This skepticism is founded on the following arguments.
1. Too many phenomena are being described as power-law or scale-free. It’s typically rather difficult to obtain good data about real-world network degree distributions. For example, the data used by Barabási and colleagues for analyzing metabolic networks came from a Web-based database to which biologists from all over the world contributed information. Such biological databases, while invaluable to research, are invariably incomplete and error-ridden. Barabási and colleagues had to rely on statistics and curve-fitting to determine the degree distributions in various metabolic networks—an imperfect method, yet the one that is most often used in analyzing real-world data. A number of networks previously identified to be “scale-free” using such techniques have later been shown to in fact have non-scale-free distributions.
As noted by philosopher and historian of biology Evelyn Fox Keller, “Current assessments of the commonality of power laws are probably overestimates.” Physicist and network scientist Cosma Shalizi had a less polite phrasing of the same sentiments: “Our tendency to hallucinate power laws is a disgrace.” As I write this, there are still considerable controversies over which real-world networks are indeed scale-free.
2. Even for networks that are actually scale-free, there are many possible causes for power law degree distributions in networks; preferential attachment is not necessarily the one that actually occurs in nature. As Cosma Shalizi succinctly said: “there turn out to be nine and sixty ways of constructing power laws, and every single one of them is right.” When I was at the Santa Fe Institute, it seemed that there was a lecture every other day on a new hypothesized mechanism that resulted in power law distributions. Some are similar to preferential attachment, some work quite differently. It’s not obvious how to decide which ones are the mechanisms that are actually causing the power laws observed in the real world.
3. The claimed significance of network science relies on models that are overly simplified and based on unrealistic assumptions. The small-world and scale-free network models are just that—models—which means that they make simplifying assumptions that might not be true of real-world networks. The hope in creating such simplified models is that they will capture at least some aspects of the phenomenon they are designed to represent. As we have seen, these two network models, in particular the scale-free model, indeed seem to capture something about degree-distributions, clustering, and resilience in a large number of real-world systems (though point 1 above suggests that the number might not be as large as some think).
However, simplified models of networks, in and of themselves, cannot explain everything about their real-world counterparts. In both the small-world and scale-free models, all nodes are assumed to be identical except for their degree; and all links are the same type and have the same strength. This is not the case in real-world networks. For example, in the real version of my social network (whose simplified model was shown in figure 14.2), some friendship links are stronger than others. Kim and Gar are both friends of mine but I know Kim much better, so I might be more likely to tell her about important personal events in my life. Furthermore, Kim is a woman and Gar is a man, which might increase my likelihood of confiding in her but not in Gar. Similarly, my friend Greg knows and cares a lot more about math than Kim, so if I wanted to share some neat mathematical fact I learned, I’d be much more likely to tell Greg about it than Kim. Such differences in link and node types as well as link strength can have very significant effects on how information spreads in a network, effects that are not captured by the simplified network models.
Information Spreading and Cascading Failure in Networks
In fact, understanding the ways in which information spreads in networks is one of the most important open problems in network science. The results I have described in this and the previous chapter are all about the structure of networks—e.g., their static degree distributions—rather than dynamics of spreading information in a network.
What do I mean by “spreading information in a network”? Here I’m using the term information to capture any kind of communication among nodes. Some examples of information spreading are the spread of rumors, gossip, fads, opinions, epidemics (in which the communication between people is via germs), electrical currents, Internet packets, neurotransmitters, calories (in the case of food webs), vote counts, and a more general network-spreading phenomenon called “cascading failure.”
The phenomenon of cascading failure emphasizes the need to understand information spreading and how it is affected by network structure. Cascading failure in a network happens as follows: Suppose each node in the network is responsible for performing some task (e.g., transmitting electrical power). If a node fails, its task gets passed on to other nodes. This can result in the other nodes getting overloaded and failing, passing on their task to still other nodes, and so forth. The result is an accelerating domino effect of failures that can bring down the entire network.
Examples of cascading failure are all too common in our networked world. Here are two fairly recent examples that made the national news:
· August 2003: A massive power outage hit the Midwestern and Northeastern United States, caused by cascading failure due to a shutdown at one generating plant in Ohio. The reported cause of the shutdown was that electrical lines, overloaded by high demand on a very hot day, sagged too far down and came into contact with overgrown trees, triggering an automatic shutdown of the lines, whose load had to be shifted to other parts of the electrical network, which themselves became overloaded and shut down. This pattern of overloading and subsequent shutdown spread rapidly, eventually resulting in about 50 million customers in the Eastern United States and Canada losing electricity, some for more than three days.
· August 2007: The computer system of the U.S. Customs and Border Protection Agency went down for nearly ten hours, resulting in more than 17,000 passengers being stuck in planes sitting on the tarmac at Los Angeles International Airport. The cause turned out to be a malfunction in a single network card on a desktop computer. Its failure quickly caused a cascading failure of other network cards, and within about an hour of the original failure, the entire system shut down. The Customs agency could not process arriving international passengers, some of whom had to wait on airplanes for more than five hours.
A third example shows that cascading failures can also happen when network nodes are not electronic devices but rather corporations.
· August-September 1998: Long-Term Capital Management (LTCM), a private financial hedge fund with credit from several large financial firms, lost nearly all of its equity value due to risky investments. The U.S. Federal Reserve feared that this loss would trigger a cascading failure in worldwide financial markets because, in order to cover its debts, LTCM would have to sell off much of its investments, causing prices of stocks and other securities to drop, which would force other companies to sell off their investments, causing a further drop in prices, et cetera. At the end of September 1998, the Federal Reserve acted to prevent such a cascading failure by brokering a bailout of LTCM by its major creditors.
The network resilience I talked about earlier—the ability of networks to maintain short average path lengths in spite of the failure of random nodes—doesn’t take into account the cascading failure scenario in which the failure of one node causes the failure of other nodes. Cascading failures provide another example of “tipping points,” in which small events can trigger accelerating feedback, causing a minor problem to balloon into a major disruption. Although many people worry about malicious threats to our world’s networked infrastructure from hackers or “cyber-terrorists,” it may be that cascading failures pose a much greater risk. Such failures are becoming increasingly common and dangerous as our society becomes more dependent on computer networks, networked voting machines, missile defense systems, electronic banking, and the like. As Andreas Antonopoulos, a scientist who studies such systems, has pointed out, “The threat is complexity itself.”
Indeed, a general understanding of cascading failures and strategies for their prevention are some of the most active current research areas in network science. Two current approaches are theories called Self-Organized Criticality(SOC) and Highly Optimized Tolerance (HOT). SOC and HOT are examples of the many theories that propose mechanisms different from preferential attachment for how scale-free networks arise. SOC and HOT each propose a general set of mechanisms for cascading failures in both evolved and engineered systems.
The simplified models of small-world networks and scale-free networks described in the previous chapter have been extraordinarily useful, as they have opened up the idea of network thinking to many different disciplines and established network science as a field in its own right. The next step is understanding the dynamics of information and other quantities in networks. To understand the dynamics of information in networks such as the immune system, ant colonies, and cellular metabolism (cf. chapter 12), network science will have to characterize networks in which the nodes and links continually change in both time and space. This will be a major challenge, to say the least. As Duncan Watts eloquently writes: “Next to the mysteries of dynamics on a network—whether it be epidemics of disease, cascading failures in power systems, or the outbreak of revolutions—the problems of networks that we have encountered up to now are just pebbles on the seashore.”