Chaos: Making a New Science - James Gleick (1988)

Inner Rhythms

The sciences do not try to explain, they hardly even try to interpret, they mainly make models. By a model is meant a mathematical construct which, with the addition of certain verbal interpretations, describes observed phenomena. The justification of such a mathematical construct is solely and precisely that it is expected to work.

—JOHN VON NEUMANN

BERNARDO HUBERMAN LOOKED OUT over his audience of assorted theoretical and experimental biologists, pure mathematicians and physicians and psychiatrists, and he realized that he had a communication problem. He had just finished an unusual talk at an unusual gathering in 1986, the first major conference on chaos in biology and medicine, under the various auspices of the New York Academy of Sciences, the National Institute of Mental Health, and the Office of Naval Research. In the cavernous Masur Auditorium at the National Institutes of Health outside Washington, Huberman saw many familiar faces, chaos specialists of long standing, and many unfamiliar ones as well. An experienced speaker could expect some audience impatience—it was the conference’s last day, and it was dangerously close to lunch time.

Huberman, a dapper black-haired Californian transplanted from Argentina, had kept up his interest in chaos since his collaborations with members of the Santa Cruz gang. He was a research fellow at the Xerox Corporation’s Palo Alto Research Center. But sometimes he dabbled in projects that did not belong to the corporate mission, and here at the biology conference he had just finished describing one of those: a model for the erratic eye movement of schizophrenics.

Psychiatrists have struggled for generations to define schizophrenia and classify schizophrenics, but the disease has been almost as difficult to describe as to cure. Most of its symptoms appear in mind and behavior. Since 1908, however, scientists have known of a physical manifestation of the disease that seems to afflict not only schizophrenics but also their relatives. When patients try to watch a slowly swinging pendulum, their eyes cannot track the smooth motion. Ordinarily the eye is a remarkably smart instrument. A healthy person’s eyes stay locked on moving targets without the least conscious thought; moving images stay frozen in place on the retina. But a schizophrenic’s eyes jump about disruptively in small increments, overshooting or undershooting the target and creating a constant haze of extraneous movements. No one knows why.

Physiologists accumulated vast amounts of data over the years, making tables and graphs to show the patterns of erratic eye motion. They generally assumed that the fluctuations came from fluctuations in the signal from the central nervous system controlling the eye’s muscles. Noisy output implied noisy input, and perhaps some random disturbances afflicting the brains of schizophrenics were showing up in the eyes. Huberman, a physicist, assumed otherwise and made a modest model.

He thought in the crudest possible way about the mechanics of the eye and wrote down an equation. There was a term for the amplitude of the swinging pendulum and a term for its frequency. There was a term for the eye’s inertia. There was a term for damping, or friction. And there were terms for error correction, to give the eye a way of locking in on the target.

As Huberman explained to his audience, the resulting equation happens to describe an analogous mechanical system: a ball rolling in a curved trough while the trough swings from side to side. The side-to-side motion corresponds to the motion of the pendulum, and the walls of the trough correspond to the error-correcting feature, tending to push the ball back toward the center. In the now-standard style of exploring such equations, Huberman had run his model for hours on a computer, changing the various parameters and making graphs of the resulting behaviors. He found both order and chaos. In some regimes, the eye would track smoothly; then, as the degree of nonlinearity was increased, the system would go through a fast period-doubling sequence and produce a kind of disorder that was indistinguishable from the disorder reported in the medical literature.

In the model, the erratic behavior had nothing to do with any outside signal. It was an inevitable consequence of too much non-linearity in the system. To some of the doctors listening, Huberman’s model seemed to match a plausible genetic model for schizophrenia. A nonlinearity that could either stabilize the system or disrupt it, depending on whether the nonlinearity was weak or strong, might correspond to a single genetic trait. One psychiatrist compared the concept to the genetics of gout, in which too high a level of uric acid creates pathological symptoms. Others, more familiar than Huberman with the clinical literature, pointed out that schizophrenics were not alone; a whole range of eye movement problems could be found in different kinds of neurological patients. Periodic oscillations, aperiodic oscillations, all sorts of dynamical behavior could be found in the data by anyone who cared to go back and apply the tools of chaos.

But for every scientist present who saw new lines of research opening up, there was another who suspected Huberman of grossly oversimplifying his model. When it came time for questions, their annoyance and frustration spilled out. “My problem is, what guides you in the modeling?” one of these scientists said. “Why look for these specific elements of nonlinear dynamics, namely these bifurcations and chaotic solutions?”

Huberman paused. “Oh, okay. Then I truly failed at stating the purpose of this. The model is simple. Someone comes to me and says, we see this, so what do you think happens. So I say, well, what is the possible explanation. So they say, well, the only thing we can come up with is something that is fluctuating over such a short time in your head. So then I say, well look, I’m a chaotician of sorts, and I know that the simplest nonlinear tracking model you can write down, the simplest, has these generic features, regardless of the details of what these things are like. So I do that and people say, oh, that’s very interesting, we never thought that perhaps this was intrinsic chaos in the system.

“The model does not have any neurophysiological data that I can even defend. All I’m saying is that the simplest tracking is something that tends to make an error and go to zero. That’s the way we move our eyes, and that’s the way an antenna tracks an airplane. You can apply this model to anything.”

Out on the floor, another biologist took the microphone, still frustrated by the stick-figure simplicity of Huberman’s model. In real eyes, he pointed out, four muscle-control systems operate simultaneously. He began a highly technical description of what he considered realistic modeling, explaining how, for example, the mass term is thrown away because the eye is heavily over-damped. “And there’s one additional complication, which is that the amount of mass present depends on the velocity of rotation, because part of the mass lags behind when the eye accelerates very rapidly. The jelly inside the eye lags behind when the outer casing rotates very fast.”

Pause. Huberman was stymied. Finally one of the conference organizers, Arnold Mandell, a psychiatrist with a long interest in chaos, took the microphone from him.

“Look, as a shrink I want to make an interpretation. What you’ve just seen is what happens when a nonlinear dynamicist working with low-dimensional global systems comes to talk to a biologist who’s been using mathematical tools. The idea that in fact there are universal properties of systems, built into the simplest representations, alienates all of us. So the question is ‘What is the subtype of the schizophrenia,’ ‘There are four ocular motor systems,’ and ‘What is the modeling from the standpoint of the actual physical structure,’ and it begins to decompose.

“What’s actually the case is that, as physicians or scientists learning all 50,000 parts of everything, we resent the possibility that there are in fact universal elements of motion. And Bernardo comes up with one and look what happens.”

Huberman said, “It happened in physics five years ago, but by now they’re convinced.”

THE CHOICE IS ALWAYS the same. You can make your model more complex and more faithful to reality, or you can make it simpler and easier to handle. Only the most naïve scientist believes that the perfect model is the one that perfectly represents reality. Such a model would have the same drawbacks as a map as large and detailed as the city it represents, a map depicting every park, every street, every building, every tree, every pothole, every inhabitant, and every map. Were such a map possible, its specificity would defeat its purpose: to generalize and abstract. Mapmakers highlight such features as their clients choose. Whatever their purpose, maps and models must simplify as much as they mimic the world.

For Ralph Abraham, the Santa Cruz mathematician, a good model is the “daisy world” of James E. Lovelock and Lynn Margulis, proponents of the so-called Gaia hypothesis, in which the conditions necessary for life are created and maintained by life itself in a self-sustaining process of dynamical feedback. The daisy world is perhaps the simplest imaginable version of Gaia, so simple as to seem idiotic. “Three things happen,” as Abraham put it, “white daisies, black daisies, and unplanted desert. Three colors: white, black, and red. How can this teach us anything about our planet? It explains how temperature regulation emerges. It explains why this planet is a good temperature for life. The daisy world model is a terrible model, but it teaches how biological homeostasis was created on earth.”

White daisies reflect light, making the planet cooler. Black daisies absorb light, lowering the albedo, or reflectivity, and thus making the planet warmer. But white daisies “want” warm weather, meaning that they thrive preferentially as temperatures rise. Black daisies want cool weather. These qualities can be expressed in a set of differential equations and the daisy world can be set in motion on a computer. A wide range of initial conditions will lead to an equilibrium attractor—and not necessarily a static equilibrium.

“It’s just a mathematical model of a conceptual model, and that’s what you want—you don’t want high-fidelity models of biological or social systems,” Abraham said. “You just put in the albedos, make some initial planting, and watch billions of years of evolution go by. And you educate children to be better members of the board of directors of the planet.”

The paragon of a complex dynamical system and to many scientists, therefore, the touchstone of any approach to complexity is the human body. No object of study available to physicists offers such a cacophony of counterrhythmic motion on scales from macroscopic to microscopic: motion of muscles, of fluids, of currents, of fibers, of cells. No physical system has lent itself to such an obsessive brand of reductionism: every organ has its own micro-structure and its own chemistry, and student physiologists spend years just on the naming of parts. Yet how ungraspable these parts can be! At its most tangible, a body part can be a seemingly well-defined organ like the liver. Or it can be a spatially challenging network of solid and liquid like the vascular system. Or it can be an invisible assembly, truly as abstract a thing as “traffic” or “democracy,” like the immune system, with its lymphocytes and T4 messengers, a miniaturized cryptography machine for encoding and decoding data about invading organisms. To study such systems without a detailed knowledge of their anatomy and chemistry would be futile, so heart specialists learn about ion transport through ventricular muscle tissue, brain specialists learn the electrical particulars of neuron firing, and eye specialists learn the name and place and purpose of each ocular muscle. In the 1980s chaos brought to life a new kind of physiology, built on the idea that mathematical tools could help scientists understand global complex systems independent of local detail. Researchers increasingly recognized the body as a place of motion and oscillation—and they developed methods of listening to its variegated drumbeat. They found rhythms that were invisible on frozen microscope slides or daily blood samples. They studied chaos in respiratory disorders. They explored feedback mechanisms in the control of red and white blood cells. Cancer specialists speculated about periodicity and irregularity in the cycle of cell growth. Psychiatrists explored a multidimensional approach to the prescription of antidepressant drugs. But surprising findings about one organ dominated the rise of this new physiology, and that was the heart, whose animated rhythms, stable or unstable, healthy or pathological, so precisely measured the difference between life and death.

EVEN DAVID RUELLE HAD STRAYED from formalism to speculate about chaos in the heart—“a dynamical system of vital interest to every one of us,” he wrote.

“The normal cardiac regime is periodic, but there are many nonperiodic pathologies (like ventricular fibrillation) which lead to the steady state of death. It seems that great medical benefit might be derived from computer studies of a realistic mathematical model which would reproduce the various cardiac dynamical regimes.”

Teams of researchers in the United States and Canada took up the challenge. Irregularities in the heartbeat had long since been discovered, investigated, isolated, and categorized. To the trained ear, dozens of irregular rhythms can be distinguished. To the trained eye, the spiky patterns of the electrocardiogram offer clues to the source and the seriousness of an irregular rhythm. A layman can gauge the richness of the problem from the cornucopia of names available for different sorts of arrhythmias. There are ectopic beats, electrical alternans, and torsades de pointes. There are high-grade block and escape rhythms. There is parasystole (atrial or ventricular, pure or modulated). There are Wenckebach rhythms (simple or complex). There is tachycardia. Most damaging of all to the prospect for survival is fibrillation. This naming of rhythms, like the naming of parts, comforts physicians. It allows specificity in diagnosing troubled hearts, and it allows some intelligence to bear on the problem. But researchers using the tools of chaos began to discover that traditional cardiology was making the wrong generalizations about irregular heartbeats, inadvertently using superficial classifications to obscure deep causes.

They discovered the dynamical heart. Almost always their backgrounds were out of the ordinary. Leon Glass of McGill University in Montreal was trained in physics and chemistry, where he indulged an interest in numbers and in irregularity, too, completing his doctoral thesis on atomic motion in liquids before turning to the problem of irregular heartbeats. Typically, he said, specialists diagnose many different arrhythmias by looking at short strips of electrocardiograms. “It’s treated by physicians as a pattern recognition problem, a matter of identifying patterns they have seen before in practice and in textbooks. They really don’t analyze in detail the dynamics of these rhythms. The dynamics are much richer than anybody would guess from reading the textbooks.”

At Harvard Medical School, Ary L. Goldberger, co-director of the arrhythmia laboratory of Beth Israel Hospital in Boston, believed that the heart research represented a threshold for collaboration between physiologists and mathematicians and physicists. “We’re at a new frontier, and a new class of phenomenology is out there,” he said. “When we see bifurcations, abrupt changes in behavior, there is nothing in conventional linear models to account for that. Clearly we need a new class of models, and physics seems to provide that.” Goldberger and other scientists had to overcome barriers of scientific language and institutional classification. A considerable obstacle, he felt, was the uncomfortable antipathy of many physiologists to mathematics. “In 1986 you won’t find the word fractals in a physiology book,” he said. “I think in 1996 you won’t be able to find a physiology book without it.”

A doctor listening to the heartbeat hears the whooshing and pounding of fluid against fluid, fluid against solid, and solid against solid. Blood courses from chamber to chamber, squeezed by the contracting muscles behind, and then stretches the walls ahead. Fibrous valves snap shut audibly against the backflow. The muscle contractions themselves depend on a complex three-dimensional wave of electrical activity. Modeling any one piece of the heart’s behavior would strain a supercomputer; modeling the whole interwoven cycle would be impossible. Computer modeling of the kind that seems natural to a fluid dynamics expert designing airplane wings for Boeing or engine flows for the National Aeronautics and Space Administration is an alien practice to medical technologists.

Trial and error, for example, has governed the design of artificial heart valves, the metal and plastic devices that now prolong the lives of those whose natural valves wear out. In the annals of engineering a special place must be reserved for nature’s own heart valve, a filmy, pliant, translucent arrangement of three tiny parachute-like cups. To let blood into the heart’s pumping chambers, the valve must fold gracefully out of the way. To keep blood from backing up when the heart pumps it forward, the valve must fill and slam closed under the pressure, and it must do so, without leaking or tearing, two or three billion times. Human engineers have not done so well. Artificial valves, by and large, have been borrowed from plumbers: standard designs like “ball in cage,” tested, at great cost, in animals. To overcome the obvious problems of leakage and stress failure was hard enough. Few could have anticipated how hard it would be to eliminate another problem. By changing the patterns of fluid flow in the heart, artificial valves create areas of turbulence and areas of stagnation; when blood stagnates, it forms clots; when clots break off and travel to the brain, they cause strokes. Such clotting was the fatal barrier to making artificial hearts. Only in the mid-1980s, when mathematicians at the Courant Institute of New York University applied new computer modeling techniques to the problem, did the design of heart valves begin to take full advantage of available technology. Their computer made motion pictures of a beating heart, two-dimensional but vividly recognizable. Hundreds of dots, representing particles of blood, stream through the valve, stretching the elastic walls of the heart and creating whirling vortices. The mathematicians found that the heart adds a whole level of complexity to the standard fluid flow problem, because any realistic model must take into account the elasticity of the heart walls themselves. Instead of flowing over a rigid surface, like air over an airplane wing, blood changes the heart surface dynamically and nonlinearly.

Even subtler, and far deadlier, was the problem of arrhythmias. Ventricular fibrillation causes hundreds of thousands of sudden deaths each year in the United States alone. In many of those cases, fibrillation has a specific, well-known trigger: blockage of the arteries, leading to the death of the pumping muscle. Cocaine use, nervous stress, hypothermia—these, too, can predispose a person to fibrillation. In many cases the onset of fibrillation remains mysterious. Faced with a patient who has survived an attack of fibrillation, a doctor would prefer to see damage—evidence of a cause. A patient with a seemingly healthy heart is actually more likely to suffer a new attack.

There is a classic metaphor for the fibrillating heart: a bag of worms. Instead of contracting and relaxing, contracting and relaxing in a repetitive, periodic way, the heart’s muscle tissue writhes, uncoordinated, helpless to pump blood. In a normally beating heart the electrical signal travels as a coordinated wave through the three-dimensional structure of the heart. When the signal arrives, each cell contracts. Then each cell relaxes for a critical refractory period, during which it cannot be set off again prematurely. In a fibrillating heart the wave breaks up. The heart is never all contracted or all relaxed.

One perplexing feature of fibrillation is that many of the heart’s individual components can be working normally. Often the heart’s pacemaking nodes continue to send out regular electrical ticks. Individual muscle cells respond properly. Each cell receives its stimulus, contracts, passes the stimulus on, and relaxes to wait for the next stimulus. In autopsy the muscle tissue may reveal no damage at all. That is one reason chaos experts believed that a new, global approach was necessary: the parts of a fibrillating heart seem to be working, yet the whole goes fatally awry. Fibrillation is a disorder of a complex system, just as mental disorders—whether or not they have chemical roots—are disorders of a complex system.

The heart will not stop fibrillating on its own. This brand of chaos is stable. Only a jolt of electricity from a defibrillation device—a jolt that any dynamicist recognizes as a massive perturbation—can return the heart to its steady state. On the whole, defibrillators are effective. But their design, like the design of artificial heart valves, has required much guesswork. “The business of determining the size and shape of that jolt has been strictly empirical,” said Arthur T. Winfree, a theoretical biologist. “There just hasn’t been any theory about that. It now appears that some assumptions are not correct. It appears that defibrillators can be radically redesigned to improve their efficiency many fold and therefore improve the chance of success many fold.” For other abnormal heart rhythms an assortment of drug therapies have been tried, also based largely on trial and error—“a black art,” as Winfree put it. Without a sound theoretical understanding of the heart’s dynamics, it is tricky to predict the effects of a given drug. “A wonderful job has been done in the last twenty years of finding out all the nitty gritty details of membrane physiology, all the detailed, precise workings of the immense complexity of all the parts of the heart. That essential part of the business is in good shape. What’s gotten overlooked is the other side, trying to achieve some global perspective on how it all works.”

WINFREE CAME FROM A FAMILY in which no one had gone to college. He got started, he would say, by not having a proper education. His father, rising from the bottom of the life insurance business to the level of vice president, moved the family almost yearly up and down the East Coast, and Winfree attended more than a dozen schools before finishing high school. He developed a feeling that the interesting things in the world had to do with biology and mathematics and a companion feeling that no standard combination of the two subjects did justice to what was interesting. So he decided not to take a standard approach. He took a five-year course in engineering physics at Cornell University, learning applied mathematics and a full range of hands-on laboratory styles. Prepared to be hired into the military-industrial complex, he got a doctorate in biology, striving to combine experiment with theory in new ways. He began at Johns Hopkins, left because of conflicts with the faculty, continued at Princeton, left because of conflicts with the faculty there, and finally was awarded a Princeton degree from a distance, when he was already teaching at the University of Chicago.

Winfree is a rare kind of thinker in the biological world, bringing a strong sense of geometry to his work on physiological problems. He began his exploration of biological dynamics in the early seventies by studying biological clocks—circadian rhythms. This was an area traditionally governed by a naturalist’s approach: this rhythm goes with that animal, and so forth. In Winfree’s view the problem of circadian rhythms should lend itself to a mathematical style of thinking. “I had a headful of nonlinear dynamics and realized that the problem could be thought of, and ought to be thought of, in those qualitative terms. Nobody had any idea what the mechanisms of biological clocks are. So you have two choices. You can wait until the biochemists figure out the mechanism of clocks and then try to derive some behavior from the known mechanisms, or you can start studying how clocks work in terms of complex systems theory and nonlinear and topological dynamics. Which I undertook to do.”

At one time he had a laboratory full of mosquitoes in cages. As any camper could guess, mosquitoes perk up around dusk each day. In a laboratory, with temperature and light kept constant to shield them from day and night, mosquitoes turn out to have an inner cycle of not twenty-four hours but twenty-three. Every twenty-three hours, they buzz around with particular intensity. What keeps them on track outdoors is the jolt of light they get each day; in effect, it resets their clock.

Winfree shined artificial light on his mosquitoes, in doses that he carefully regulated. These stimuli either advanced or delayed the next cycle, and he plotted the effect against the timing of the blast. Then, instead of trying to guess at the biochemistry involved, he looked at the problem topologically—that is, he looked at the qualitative shape of the data, instead of the quantitative details. He came to a startling conclusion: There was a singularity in the geometry, a point different from all the other points. Looking at the singularity, he predicted that one special, precisely timed burst of light would cause a complete breakdown of a mosquito’s biological clock, or any other biological clock.

The prediction was surprising, but Winfree’s experiments bore it out. “You go to a mosquito at midnight and give him a certain number of photons, and that particularly well-timed jolt turns off the mosquito’s clock. He’s an insomniac after that—he’ll doze, buzz for a while, all at random, and he’ll continue doing that for as long as you care to watch, or until you come along with another jolt. You’ve given him perpetual jet lag.” In the early seventies Winfree’s mathematical approach to circadian rhythms stirred little general interest, and it was hard to extend the laboratory technique to species that would object to sitting in little cages for months at a time.

Human jet lag and insomnia remain on the list of unsolved problems in biology. Both bring out the worst charlatanism—useless pills and nostrums. Researchers did amass data on human subjects, usually students or retired people, or playwrights with plays to finish, willing to accept a few hundred dollars a week to live in “time isolation”: no daylight, no temperature change, no clocks, and no telephones. People have a sleep-wake cycle and also a body-temperature cycle, both nonlinear oscillators that restore themselves after slight perturbations. In isolation, without a daily resetting stimulus, the temperature cycle seems to be about twenty-five hours, with the low occurring during sleep. But experiments by German researchers found that after some weeks the sleep-wake cycle would detach itself from the temperature cycle and become erratic. People would stay awake for twenty or thirty hours at a time, followed by ten or twenty hours of sleep. Not only would the subjects remain unaware that their day had lengthened, they would refuse to believe it when told. Only in the mid-1980s, though, did researchers begin to apply Winfree’s systematic approach to humans, starting with an elderly woman who did needlepoint in the evening in front of banks of bright light. Her cycle changed sharply, and she reported feeling great, as if she were driving in a car with the top down. As for Winfree, he had moved on to the subject of rhythms in the heart.

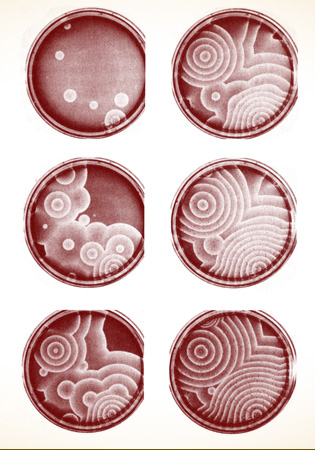
CHEMICAL CHAOS. Waves propagating outward in concentric circles and even spiral waves were signs of chaos in a widely studied chemical reaction, the Beluzov-Zhabotinsky reaction. Similar patterns have been observed in dishes of millions of amoeba. Arthur Winfree theorized that such waves are analogous to the waves of electrical activity coursing through heart muscles, regularly or erratically.

Actually, he would not have said “moved on.” To Winfree it was the same subject—different chemistry, same dynamics. He had gained a specific interest in the heart, however, after he helplessly witnessed the sudden cardiac deaths of two people, one a relative on a summer vacation, the other a man in a pool where Winfree was swimming. Why should a rhythm that has stayed on track for a lifetime, two billion or more uninterrupted cycles, through relaxation and stress, acceleration and deceleration, suddenly break into an uncontrolled, fatally ineffectual frenzy?

WINFREE TOLD THE STORY of an early researcher, George Mines, who in 1914 was twenty-eight years old. In his laboratory at McGill University in Montreal, Mines made a small device capable of delivering small, precisely regulated electrical impulses to the heart.

“When Mines decided it was time to begin work with human beings, he chose the most readily available experimental subject: himself,” Winfree wrote. “At about six o’clock that evening, a janitor, thinking it was unusually quiet in the laboratory, entered the room. Mines was lying under the laboratory bench surrounded by twisted electrical equipment. A broken mechanism was attached to his chest over the heart and a piece of apparatus nearby was still recording the faltering heartbeat. He died without recovering consciousness.”

One might guess that a small but precisely timed shock can throw the heart into fibrillation, and indeed even Mines had guessed it, shortly before his death. Other shocks can advance or retard the next beat, just as in circadian rhythms. But one difference between hearts and biological clocks, a difference that cannot be set aside even in a simplified model, is that a heart has a shape in space. You can hold it in your hand. You can track an electrical wave through three dimensions.

To do so, however, requires ingenuity. Raymond E. Ideker of Duke University Medical Center read an article by Winfree in Scientific American in 1983 and noted four specific predictions about inducing and halting fibrillation based on nonlinear dynamics and topology. Ideker didn’t really believe them. They seemed too speculative and, from a cardiologist’s point of view, so abstract. Within three years, all four had been tested and confirmed, and Ideker was conducting an advanced program to gather the richer data necessary to develop the dynamical approach to the heart. It was, as Winfree said, “the cardiac equivalent of a cyclotron.”

The traditional electrocardiogram offers only a gross one-dimensional record. During heart surgery a doctor can take an electrode and move it from place to place on the heart, sampling as many as fifty or sixty sites over a ten-minute period and thus producing a sort of composite picture. During fibrillation this technique is useless. The heart changes and quivers far too rapidly. Ideker’s technique, depending heavily on real-time computer processing, was to embed 128 electrodes in a web that he would place over a heart like a sock on a foot. The electrodes recorded the voltage field as each wave traveled through the muscle, and the computer produced a cardiac map.

Ideker’s immediate intention, beyond testing Winfree’s theoretical ideas, was to improve the electrical devices used to halt fibrillation. Emergency medical teams carry standard versions of defibrillators, ready to deliver a strong DC shock across the thorax of a stricken patient. Experimentally, cardiologists have developed a small implantable device to be sewn inside the chest cavity of patients thought to be especially at risk, although identifying such patients remains a challenge. An implantable defibrillator, somewhat bigger than a pacemaker, sits and waits, listening to the steady heartbeat, until it becomes necessary to release a burst of electricity. Ideker began to assemble the physical understanding necessary to make the design of defibrillators less a high-priced guessing game, more a science.

WHY SHOULD THE LAWS of chaos apply to the heart, with its peculiar tissue—cells forming interconnected branching fibers, transporting ions of calcium, potassium, and sodium? That was the question puzzling scientists at McGill and the Massachusetts Institute of Technology.

Leon Glass and his colleagues Michael Guevara and Alvin Schrier at McGill carried out one of the most talked-about lines of research in the whole short history of nonlinear dynamics. They used tiny aggregates of heart cells from chicken embryos seven days old. These balls of cells, 1/200 of an inch across, placed in a dish and shaken together, began beating spontaneously at rates on the order of once a second, with no outside pacemaker at all. The pulsation was clearly visible through a microscope. The next step was to apply an external rhythm as well, and the McGill scientists did this through a microelectrode, a thin tube of glass drawn out to a fine point and inserted into one of the cells. An electric potential was passed through the tube, stimulating the cells with a strength and a rhythm that could be adjusted at will.

They summed up their findings this way in Science in 1981: “Exotic dynamic behavior that was previously seen in mathematical studies and in experiments in the physical sciences may in general be present when biological oscillators are periodically perturbed.” They saw period-doubling—beat patterns that would bifurcate and bifurcate again as the stimulus changed. They made Poincaré maps and circle maps. They studied intermittency and mode-locking. “Many different rhythms can be established between a stimulus and a little piece of chicken heart,” Glass said. “Using nonlinear mathematics, we can understand quite well the different rhythms and their orderings. Right now, the training of cardiologists has almost no mathematics, but the way we are looking at these problems is the way that at some point in the future people will have to look at these problems.”

Meanwhile, in a joint Harvard-M.I.T. program in health sciences and technology, Richard J. Cohen, a cardiologist and a physicist, found a range of period-doubling sequences in experiments with dogs. Using computer models, he tested one plausible scenario, in which the wavefront of electrical activity breaks up on islands of tissue. “It is a clear instance of the Feigenbaum phenomenon,” he said, “a regular phenomenon which, under certain circumstances, becomes chaotic, and it turns out that the electrical activity in the heart has many parallels with other systems that develop chaotic behavior.”

The McGill scientists also went back to old data accumulated on different kinds of abnormal heartbeats. In one well-known syndrome, abnormal, ectopic beats are interspersed with normal, sinus beats. Glass and his colleagues examined the patterns, counting the numbers of sinus beats between ectopic beats. In some people, the numbers would vary, but for some reason they would always be odd: 3 or 5 or 7. In other people, the number of normal beats would always be part of the sequence: 2, 5, 8, 11….

“People have made these weird numerology observations, but the mechanisms are not very easy to understand,” Glass said. “There is often some type of regularity in these numbers, but there is often great irregularity also. It’s one of the slogans in this business: order in chaos.”

Traditionally, thoughts about fibrillation took two forms. One classic idea was that secondary pacemaking signals come from abnormal centers within the heart muscle itself, conflicting with the main signal. These tiny ectopic centers fire out waves at uncomfortable intervals, and the interplay and overlapping has been thought to break up the coordinated wave of contraction. The research by the McGill scientists provided some support for this idea, by demonstrating that a full range of dynamical misbehavior can arise from the interplay between an external pulse and a rhythm inherent in the heart tissue. But why secondary pacemaking centers should develop in the first place has remained hard to explain.

The other approach focused not on the initiation of electrical waves but on the way they are conducted geographically through the heart, and the Harvard-M.I.T. researchers remained closer to this tradition. They found that abnormalities in the wave, spinning in tight circles, could cause “re-entry,” in which some areas begin a new beat too soon, preventing the heart from pausing for the quiet interval necessary to maintain coordinated pumping.

By stressing the methods of nonlinear dynamics, both groups of researchers were able to use the awareness that a small change in one parameter—perhaps a change in timing or electrical conductivity—could push an otherwise healthy system across a bifurcation point into a qualitatively new behavior. They also began to find common ground for studying heart problems globally, linking disorders that were previously considered unrelated. Furthermore, Winfree believed that, despite their different focus, both the ectopic beat school and the re-entry school were right. His topological approach suggested that the two ideas might be one and the same.

“Dynamical things are generally counterintuitive, and the heart is no exception,” Winfree said. Cardiologists hoped that the research would lead to a scientific way of identifying those at risk for fibrillation, designing defibrillating devices, and prescribing drugs. Winfree hoped, too, that a global, mathematical perspective on such problems would fertilize a discipline that barely existed in the United States, theoretical biology.

NOW SOME PHYSIOLOGISTS SPEAK of dynamical diseases: disorders of systems, breakdowns in coordination or control. “Systems that normally oscillate, stop oscillating, or begin to oscillate in a new and unexpected fashion, and systems that normally do not oscillate, begin oscillating,” was one formulation. These syndromes include breathing disorders: panting, sighing, Cheyne-Stokes respiration, and infant apnea—linked to sudden infant death syndrome. There are dynamical blood disorders, including a form of leukemia, in which disruptions alter the balance of white and red cells, platelets and lymphocytes. Some scientists speculate that schizophrenia itself might belong in this category, along with some forms of depression.

But physiologists have also began to see chaos as health. It has long been understood that nonlinearity in feedback processes serves to regulate and control. Simply put, a linear process, given a slight nudge, tends to remain slightly off track. A nonlinear process, given the same nudge, tends to return to its starting point. Christian Huygens, the seventeenth-century Dutch physicist who helped invent both the pendulum clock and the classical science of dynamics, stumbled upon one of the great examples of this form of regulation, or so the standard story goes. Huygens noticed one day that a set of pendulum clocks placed against a wall happened to be swinging in perfect chorus-line synchronization. He knew that the clocks could not be that accurate. Nothing in the mathematical description then available for a pendulum could explain this mysterious propagation of order from one pendulum to another. Huygens surmised, correctly, that the clocks were coordinated by vibrations transmitted through the wood. This phenomenon, in which one regular cycle locks into another, is now called entrainment, or mode locking. Mode locking explains why the moon always faces the earth, or more generally why satellites tend to spin in some whole-number ratio of their orbital period: 1 to 1, or 2 to 1, or 3 to 2. When the ratio is close to a whole number, nonlinearity in the tidal attraction of the satellite tends to lock it in. Mode locking occurs throughout electronics, making it possible, for example, for a radio receiver to lock in on signals even when there are small fluctuations in their frequency. Mode locking accounts for the ability of groups of oscillators, including biological oscillators, like heart cells and nerve cells, to work in synchronization. A spectacular example in nature is a Southeast Asian species of firefly that congregates in trees during mating periods, thousands at one time, blinking in a fantastic spectral harmony.

With all such control phenomena, a critical issue is robustness: how well can a system withstand small jolts. Equally critical in biological systems is flexibility: how well can a system function over a range of frequencies. A locking-in to a single mode can be enslavement, preventing a system from adapting to change. Organisms must respond to circumstances that vary rapidly and unpredictably; no heartbeat or respiratory rhythm can be locked into the strict periodicities of the simplest physical models, and the same is true of the subtler rhythms of the rest of the body. Some researchers, among them Ary Goldberger of Harvard Medical School, proposed that healthy dynamics were marked by fractal physical structures, like the branching networks of bronchial tubes in the lung and conducting fibers in the heart, that allow a wide range of rhythms. Thinking of Robert Shaw’s arguments, Goldberger noted: “Fractal processes associated with scaled, broadband spectra are ‘information-rich.’ Periodic states, in contrast, reflect narrow-band spectra and are defined by monotonous, repetitive sequences, depleted of information content.” Treating such disorders, he and other physiologists suggested, may depend on broadening a system’s spectral reserve, its ability to range over many different frequencies without falling into a locked periodic channel.

Arnold Mandell, the San Diego psychiatrist and dynamicist who came to Bernardo Huberman’s defense over eye movement in schizophrenics, went even further on the role of chaos in physiology. “Is it possible that mathematical pathology, i.e. chaos, is health? And that mathematical health, which is the predictability and differentiability of this kind of a structure, is disease?” Mandell had turned to chaos as early as 1977, when he found “peculiar behavior” in certain enzymes in the brain that could only be accounted for by the new methods of nonlinear mathematics. He had encouraged the study of the oscillating three-dimensional entanglements of protein molecules in the same terms; instead of drawing static structures, he argued, biologists should understand such molecules as dynamical systems, capable of phase transitions. He was, as he said himself, a zealot, and his main interest remained the most chaotic organ of all. “When you reach an equilibrium in biology you’re dead,” he said. “If I ask you whether your brain is an equilibrium system, all I have to do is ask you not to think of elephants for a few minutes, and you know it isn’t an equilibrium system.”

CHAOTIC HARMONIES. The interplay of different rhythms. such as radio frequencies or planetary orbits, produces a special version of chaos. Below and on the facing page, computer pictures of some of the “attractors” that can result when three rhythms come together.

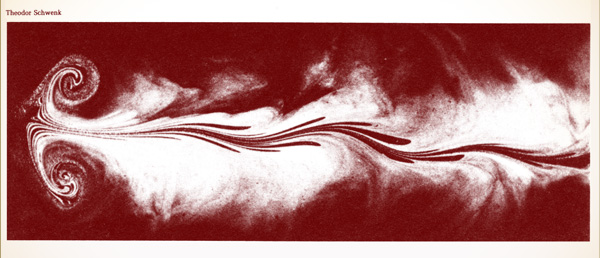
CHAOTIC FLOWS. A rod drawn through viscous fluid causes a simple, wavy form. If drawn several times, more complicated forms arise.

To Mandell, the discoveries of chaos dictate a shift in clinical approaches to treating psychiatric disorders. By any objective measure, the modern business of “psychopharmacology”—the use of drugs to treat everything from anxiety and insomnia to schizophrenia itself—has to be judged a failure. Few patients, if any, are cured. The most violent manifestations of mental illness can be controlled, but with what long-term consequences, no one knows. Mandell offered his colleagues a chilling assessment of the most commonly used drugs. Phenothiazines, prescribed for schizophrenics, make the fundamental disorder worse. Tricyclic anti-depressants “increase the rate of mood cycling, leading to long-term increases in numbers of relapsing psychopathologic episodes.” And so on. Only lithium has any real medical success, Mandell said, and only for some disorders.

As he saw it, the problem was conceptual. Traditional methods for treating this “most unstable, dynamic, infinite-dimensional machine” were linear and reductionist. “The underlying paradigm remains: one gene → one peptide → one enzyme → one neurotransmitter → one receptor → one animal behavior → one clinical syndrome → one drug → one clinical rating scale. It dominates almost all research and treatment in psychopharmacology. More than 50 transmitters, thousands of cell types, complex electromagnetic phenomenology, and continuous instability based autonomous activity at all levels, from proteins to the electroencephalogram—and still the brain is thought of as a chemical point-to-point switchboard.” To someone exposed to the world of nonlinear dynamics the response could only be: How naive. Mandell urged his colleagues to understand the flowing geometries that sustain complex systems like the mind.

Many other scientists began to apply the formalisms of chaos to research in artificial intelligence. The dynamics of systems wandering between basins of attraction, for example, appealed to those looking for a way to model symbols and memories. A physicist thinking of ideas as regions with fuzzy boundaries, separate yet overlapping, pulling like magnets and yet letting go, would naturally turn to the image of a phase space with “basins of attraction.” Such models seemed to have the right features: points of stability mixed with instability, and regions with changeable boundaries. Their fractal structure offered the kind of infinitely self-referential quality that seems so central to the mind’s ability to bloom with ideas, decisions, emotions, and all the other artifacts of consciousness. With or without chaos, serious cognitive scientists can no longer model the mind as a static structure. They recognize a hierarchy of scales, from neuron upward, providing an opportunity for the interplay of microscale and macroscale so characteristic of fluid turbulence and other complex dynamical processes.

Pattern born amid formlessness: that is biology’s basic beauty and its basic mystery. Life sucks order from a sea of disorder. Erwin Schrödinger, the quantum pioneer and one of several physicists who made a nonspecialist’s foray into biological speculation, put it this way forty years ago: A living organism has the “astonishing gift of concentrating a ‘stream of order’ on itself and thus escaping the decay into atomic chaos.” To Schrödinger, as a physicist, it was plain that the structure of living matter differed from the kind of matter his colleagues studied. The building block of life—it was not yet called DNA—was an aperiodic crystal. “In physics we have dealt hitherto only with periodic crystals. To a humble physicist’s mind, these are very interesting and complicated objects; they constitute one of the most fascinating and complex material structures by which inanimate nature puzzles his wits. Yet, compared with the aperiodic crystal, they are rather plain and dull.” The difference was like the difference between wallpaper and tapestry, between the regular repetition of a pattern and the rich, coherent variation of an artist’s creation. Physicists had learned only to understand wallpaper. It was no wonder they had managed to contribute so little to biology.

Schrödinger’s view was unusual. That life was both orderly and complex was a truism; to see aperiodicity as the source of its special qualities verged on mystical. In Schrödinger’s day, neither mathematics nor physics provided any genuine support for the idea. There were no tools for analyzing irregularity as a building block of life. Now those tools exist.