Chaos: Making a New Science - James Gleick (1988)

The Dynamical Systems Collective

Communication across the revolutionary divide is inevitably partial.

—THOMAS S. KUHN

SANTA CRUZ was the newest campus in the University of California system, carved into storybook scenery an hour south of San Francisco, and people sometimes said that it looked more like a national forest than a college. The buildings were nestled among redwoods, and, in the spirit of the time, the planners endeavored to leave every tree standing. Little footpaths ran from place to place. The whole campus lay atop a hill, so that every so often you would happen upon the view south across the sparkling waves of Monterey Bay. Santa Cruz opened in 1966, and within a few years it became, briefly, the most selective of the California campuses. Students associated it with many of the icons of the intellectual avant-garde: Norman O. Brown, Gregory Bateson, and Herbert Marcuse lectured there, and Tom Lehrer sang. The school’s graduate departments, building from scratch, began with an ambivalent outlook, and physics was no exception. The faculty—about fifteen physicists—was energetic and mostly young, suited to the mix of bright nonconformists attracted to Santa Cruz. They were influenced by the free-thinking ideology of the time; yet they also, the physicists, looked southward toward Caltech and realized that they needed to establish standards and demonstrate their seriousness.

One graduate student whose seriousness no one doubted was Robert Stetson Shaw, a bearded Boston native and Harvard graduate, the oldest of six children of a doctor and a nurse, who in 1977 was about to turn thirty-one years old. That made him a little older than most graduate students, his Harvard career having been interrupted several times for Army service, commune living, and other impromptu experiences somewhere between those extremes. He did not know why he came to Santa Cruz. He had never seen the campus, although he had seen a brochure, with pictures of the redwoods and language about trying new educational philosophies. Shaw was quiet—shy, in a forceful sort of way. He was a good student, and he had reached a point just, a few months away from completing his doctoral thesis on superconductivity. No one was particularly concerned that he was wasting time downstairs in the physics building playing with an analog computer.

The education of a physicist depends on a system of mentors and protégés. Established professors get research assistants to help with laboratory work or tedious calculations. In return the graduate students and postdoctoral fellows get shares of their professors’ grant money and bits of publication credit. A good mentor helps his student choose problems that will be both manageable and fruitful. If the relationship prospers, the professor’s influence helps his protégé find employment. Often their names will be forever linked. When a science does not yet exist, however, few people are ready to teach it. In 1977 chaos offered no mentors. There were no classes in chaos, no centers for nonlinear studies and complex systems research, no chaos textbooks, nor even a chaos journal.

WILLIAM BURKE, A SANTA CRUZ COSMOLOGIST and relativist, ran into his friend Edward A. Spiegel, an astrophysicist, at one o’clock in the morning in the lobby of a Boston hotel, where they were attending a conference on general relativity. “Hey, I’ve just been listening to the Lorenz attractor,” Spiegel said. Spiegel had transmuted this emblem of chaos, using some impromptu circuitry connected to a hi-fi set, into a looping slide-whistle antimelody. He brought Burke into the bar for a drink and explained.

Spiegel knew Lorenz personally, and he had known about chaos since the 1960s. He had made it his business to pursue clues to the possibility of erratic behavior in models of star motion, and he kept in touch with the French mathematicians. Eventually, as a professor at Columbia University, he made turbulence in space—“cosmic arrhythmias”—the focus of his astronomical study. He had a flair for captivating his colleagues with new ideas, and as the night wore on he captivated Burke. Burke was open to such things. He had made his reputation by working through one of Einstein’s more paradoxical gifts to physics, the notion of gravity waves rippling through the fabric of space-time. It was a highly nonlinear problem, with misbehavior related to the troublesome nonlinearities in fluid dynamics. It was also properly abstract and theoretical, but Burke liked down-to-earth physics, too, at one point publishing a paper on the optics of beer glasses: how thick could you make the glass and still leave the appearance of a full portion of beer. He liked to say that he was a bit of a throwback who considered physics to be reality. Furthermore, he had read Robert May’s paper in Nature, with its plaintive plea for more education about simple nonlinear systems, and he, too, had taken a few hours to play with May’s equations on a calculator. So the Lorenz attractor sounded interesting. He had no intention of listening to it. He wanted to see it. When he returned to Santa Cruz, he handed Rob Shaw a piece of paper on which he had scrawled a set of three differential equations. Could Shaw put these on the analog computer?

In the evolution of computers, analog machines represented a blind alley. They did not belong in physics departments, and the existence of such things at Santa Cruz was pure happenstance: the original plansfor Santa Cruz had included an engineering school; by the time the engineering school was canceled, an eager purchasing agent had already bought some equipment. Digital computers, built up from circuitry that switched off or on, zero or one, no or yes, gave precise answers to the questions programmers asked, and they proved far more amenable to the miniaturization and acceleration of technology that ruled the computer revolution. Anything done once on a digital computer could be done again, with exactly the same result, and in principle could be done on any other digital computer. Analog computers were, by design, fuzzy. Their building blocks were not yes-no switches but electronic circuits like resistors and capacitors—instantly familiar to anyone who played with radios in the era before solid-state, as Shaw had. The machine at Santa Cruz was a Systron-Donner, a heavy, dusty thing with a patch panel for its front, like the patch panels used by old-fashioned telephone switchboards. Programming the analog computer was a matter of choosing electronic components and plugging cords into the patch panel.

By building up various combinations of circuitry, a programmer simulates systems of differential equations in ways that happen to be well-suited to engineering problems. Say you want to model an automobile suspension with springs, dampers, and mass, to design the smoothest ride. Oscillations in the circuitry can be made to correspond to the oscillations in the physical system. A capacitor takes the place of a spring, inductors represent mass, and so forth. The calculations are not precise. Numerical computation is sidestepped. Instead you have a model made of metal and electrons, quite fast and—best of all—easily adjustable. Simply by turning knobs, you can adjust variables, making the spring stronger or the friction weaker. And you can watch the results change in real time, patterns traced across the screen of an oscilloscope.

Upstairs in the superconductivity laboratory, Shaw was making his desultory way to the end of his thesis work. But he was beginning to spend more and more time playing with the Systron-Donner. He had got far enough to see phase-space portraits of some simple systems—representations of periodic orbits, or limit cycles. If he had seen chaos, in the form of strange attractors, he certainly had not recognized it. The Lorenz equations, handed to him on a piece of paper, were no more complicated than the systems he had been tinkering with. It took just a few hours to patch in the right cords and adjust the knobs. A few minutes later, Shaw knew that he would never finish his superconductivity thesis.

He spent several nights in that basement, watching the green dot of the oscilloscope flying around the screen, tracing over and over the characteristic owl’s mask of the Lorenz attractor. The flow of the shape stayed on the retina, a flickering, fluttering thing, unlike any object Shaw’s research had shown him. It seemed to have a life of its own. It held the mind just as a flame does, by running in patterns that never repeat. The imprecision and not-quite-repeatability of the analog computer worked to Shaw’s advantage. He quickly saw the sensitive dependence on initial conditions that persuaded Edward Lorenz of the futility of longterm weather forecasting. He would set the initial conditions, push the go button, and off the attractor would go. Then he would set the same initial conditions again—as close as physically possible—and the orbit would sail merrily away from its previous course, yet end up on the same attractor.

As a child, Shaw had illusions of what science would be like—dashing off romantically into the unknown. This was finally a kind of exploration that lived up to his illusions. Low-temperature physics was fun from a tinkerer’s point of view, with plenty of plumbing and big magnets, liquid helium and dials. But for Shaw it was leading nowhere. Soon he moved the analog computer upstairs, and the room was never used for superconductivity again.

“ALL YOU HAVE TO DO is put your hands on these knobs, and suddenly you are exploring in this other world where you are one of the first travelers and you don’t want to come up for air,” said Ralph Abraham, a professor of mathematics who dropped by in the early days to watch the Lorenz attractor in motion. He had been with Steve Smale in the most glorious early days at Berkeley, and so he was one of very few members of the Santa Cruz faculty with a background that would let him grasp the significance of Shaw’s game-playing. His first reaction was astonishment at the speed of the display—and Shaw pointed out that he was using extra capacitors to keep it from running even faster. The attractor was robust, too. The imprecision of the analog circuitry proved that—the tuning and tweaking of knobs did not make the attractor vanish, did not turn it into something random, but turned it or bent it in ways that slowly began to make sense. “Rob had the spontaneous experience where a little exploration reveals all the secrets,” Abraham said. “All the important concepts—the Lyapunov exponent, the fractal dimension—would just naturally occur to you. You would see it and start exploring.”

Was this science? It certainly was not mathematics, this computer work with no formalisms or proofs, and no amount of sympathetic encouragement from people like Abraham could change that. The physics faculty saw no reason to think it was physics, either. Whatever it was, it drew an audience. Shaw usually left his door open, and it happened that the entrance to the physics department was just across the hall. The foot traffic was considerable. Before long, he found himself with company.

The group that came to call itself the Dynamical Systems Collective—others sometimes called it the Chaos Cabal—depended on Shaw as its quiet center. He suffered from a certain diffidence in putting his ideas forward in the academic marketplace; fortunately for him, his new associates had no such problem. They, meanwhile, often returned to his steady vision of how to carry out an unplanned program of exploring an unrecognized science.

Doyne Farmer, a tall, angular, and sandy-haired Texas native, became the group’s most articulate spokesman. In 1977 he was twenty-four years old, all energy and enthusiasm, a machine for ideas. Those who met him sometimes suspected at first that he was all hot air. Norman Packard, three years younger, a boyhood friend who had grown up in the same New Mexico town, Silver City, arrived at Santa Cruz that fall, just as Farmer was beginning a year off to devote all his energy to his plan for applying the laws of motion to the game of roulette. This enterprise was as earnest as it was far-fetched. For more than a decade Farmer and a changing cast of fellow physicists, professional gamblers, and hangers-on pursued the roulette dream. Farmer did not give it up even after he joined the Theoretical Division of Los Alamos National Laboratory. They calculated tilts and trajectories, wrote and rewrote custom software, embedded computers in shoes and made nervous forays into gambling casinos. But nothing quite worked as planned. At one time or another, all the members of the collective but Shaw lent their energy to roulette, and it had to be said that the project gave them unusual training in the rapid analysis of dynamical systems, but it did little to reassure the Santa Cruz physics faculty that Farmer was taking science seriously.

The fourth member of the group was James Crutchfield, the youngest and the only native Californian. He was short and powerfully built, a stylish windsurfer and, most important for the collective, an instinctive master of computing. Crutchfield came to Santa Cruz as an undergraduate, worked as a laboratory assistant on Shaw’s pre-chaos superconductivity experiments, spent a year commuting “over the hill,” as they said in Santa Cruz, to a job at IBM’s research center in San Jose, and did not actually join the physics department as a graduate student until 1980. By then he had spent two years hanging around Shaw’s laboratory and rushing to pick up the mathematics he needed to understand dynamical systems. Like the rest of the group, he left the department’s standard track behind.

It was spring in 1978 before the department quite believed that Shaw was abandoning his superconductivity thesis. He was so close to finishing. No matter how bored he was, the faculty reasoned that he could rush through the formalities, get his doctorate and move on to the real world. As for chaos, there were questions of academic suitability. No one at Santa Cruz was qualified to supervise a course of study in this field-without-a-name. No one had ever received a doctorate in it. Certainly no jobs were available for graduates with this kind of specialty. There was also the matter of money. Physics at Santa Cruz, as at every American university, was financed mostly by the National Science Foundation and other agencies of the federal government through research grants to members of the faculty. The Navy, the Air Force, the Department of Energy, the Central Intelligence Agency—all dispensed vast sums for pure research, without necessarily caring about immediate application to hydrodynamics, aerodynamics, energy, or intelligence. A faculty physicist would get enough to pay for laboratory equipment and the salaries of research assistants—graduate students, who would piggy-back themselves on his grant. He would pay for their photocopying, for their travel to meetings, even for salaries to keep them going in the summers. Otherwise a student was financially adrift. This was the system from which Shaw, Farmer, Packard, and Crutchfield now cut themselves off.

When certain kinds of electronic equipment began to disappear at night, it became prudent to look for them in Shaw’s former low-temperature laboratory. Occasionally a member of the collective would be able to cadge a hundred dollars from the graduate student association, or the physics department would find a way to appropriate that much. Plotters, converters, electronic filters began to accumulate. A particle physics group down the hall had a small digital computer that was destined for the scrapheap; it found its way to Shaw’s lab. Farmer became a particular specialist in scrounging computer time. One summer he was invited to the National Center for Atmospheric Research in Boulder, Colorado, where huge computers handle research on such tasks as global weather modeling, and his ability to siphon expensive time from these machines stunned the climatologists.

The Santa Cruzians’ tinkering sensibility served them well. Shaw had grown up “gizmo-oriented.” Packard had fixed television sets as a boy in Silver City. Crutchfield belonged to the first generation of mathematicians for whom the logic of computer processors was a natural language. The physics building itself, in its shady redwood setting, was like physics buildings everywhere, with a universal ambience of cement floors and walls that always needed repainting, but the room taken over by the chaos group developed its own atmosphere, with piles of papers and pictures of Tahitian islanders on the walls and, eventually, printouts of strange attractors. At almost any hour, though night was a safer bet than morning, a visitor could see members of the group rearranging circuitry, yanking out patch cords, arguing about consciousness or evolution, adjusting an oscilloscope display, or just staring while a glowing green spot traced a curve of light, its orbit flickering and seething like something alive.

“THE SAME THING REALLY DREW all of us: the notion that you could have determinism but not really,” Farmer said. “The idea that all these classical deterministic systems we’d learned about could generate randomness was intriguing. We were driven to understand what made that tick.

“You can’t appreciate the kind of revelation that is unless you’ve been brainwashed by six or seven years of a typical physics curriculum. You’re taught that there are classical models where everything is determined by initial conditions, and then there are quantum mechanical models where things are determined but you have to contend with a limit on how much initial information you can gather. Nonlinear was a word that you only encountered in the back of the book. A physics student would take a math course and the last chapter would be on nonlinear equations. You would usually skip that, and, if you didn’t, all they would do is take these nonlinear equations and reduce them to linear equations, so you just get approximate solutions anyway. It was just an exercise in frustration.

“We had no concept of the real difference that nonlinearity makes in a model. The idea that an equation could bounce around in an apparently random way—that was pretty exciting. You would say, ‘Where is this random motion coming from? I don’t see it in the equations.’ It seemed like something for nothing, or something out of nothing.”

Crutchfield said, “It was a realization that here is a whole realm of physical experience that just doesn’t fit in the current framework. Why wasn’t that part of what we were taught? We had a chance to look around the immediate world—a world so mundane it was wonderful—and understand something.”

They enchanted themselves and dismayed their professors with leaps to questions of determinism, the nature of intelligence, the direction of biological evolution.

“The glue that held us together was a long-range vision,” Packard said, “It was striking to us that if you take regular physical systems which have been analyzed to death in classical physics, but you take one little step away in parameter space, you end up with something to which all of this huge body of analysis does not apply.

“The phenomenon of chaos could have been discovered long, long ago. It wasn’t, in part because this huge body of work on the dynamics of regular motion didn’t lead in that direction. But if you just look, there it is. It brought home the point that one should allow oneself to be guided by the physics, by observations, to see what kind of theoretical picture one could develop. In the long run we saw the investigation of complicated dynamics as an entry point that might lead to an understanding of really, really complicated dynamics.”

Farmer said, “On a philosophical level, it struck me as an operational way to define free will, in a way that allowed you to reconcile free will with determinism. The system is deterministic, but you can’t say what it’s going to do next. At the same time, I’d always felt that the important problems out there in the world had to do with the creation of organization, in life or intelligence. But how did you study that? What biologists were doing seemed so applied and specific; chemists certainly weren’t doing it; mathematicians weren’t doing it at all, and it was something that physicists just didn’t do. I always felt that the spontaneous emergence of self-organization ought to be part of physics.

“Here was one coin with two sides. Here was order, with randomness emerging, and then one step further away was randomness with its own underlying order.”

SHAW AND HIS COLLEAGUES had to turn their raw enthusiasm into a scientific program. They had to ask questions that could be answered and that would be worth answering. They sought ways of connecting theory and experiment—there, they felt, was a gap that needed to be closed. Before they could even begin, they had to learn what was known and what was not, and this itself was a formidable challenge.

They were hindered by the tendency of communication to travel piecemeal in science, particularly when a new subject jumps across the established subdisciplines. Often they had no idea whether they were on new or old territory. One invaluable antidote to their ignorance was Joseph Ford, an advocate of chaos at the Georgia Institute of Technology. Ford had already decided that nonlinear dynamics was the future of physics—the entire future—and had set himself up as a clearinghouse of information on journal articles. His background was in nondissipative chaos, the chaos of astronomical systems or of particle physics. He had an unusually intimate knowledge of the work being done by the Soviet school, and he made it his business to seek out connections with anyone who remotely shared the philosophical spirit of this new enterprise. He had friends everywhere. Any scientist who sent in a paper on nonlinear science would have his work summarized on Ford’s growing list of abstracts. The Santa Cruz students found out about Ford’s list and made up a form postcard for requesting prepublication copies of articles. Soon the preprints flooded in.

They realized that many sorts of questions could be asked about strange attractors. What are their characteristic shapes? What is their topological structure? What does the geometry reveal about the physics of the related dynamical systems? The first approach was the hands-on exploration that Shaw began with. Much of the mathematical literature dealt directly with structure, but the mathematical approach struckShaw as too detailed—still too many trees and not enough forest. As he worked his way through the literature, he felt that the mathematicians, deprived by their own traditions of the new tools of computing, had been buried in the particular complexities of orbit structures, infinities here and discontinuities there. The mathematicians had not cared especially about analog fuzziness—from the physicist’s point of view, the fuzziness that surely controlled real-world systems. Shaw saw on his oscilloscope not the individual orbits but an envelope in which the orbits were embedded. It was the envelope that changed as he gently turned the knobs. He could not give a rigorous explanation of the folds and twists in the language of mathematical topology. Yet he began to feel that he understood them.

A physicist wants to make measurements. What was there in these elusive moving images to measure? Shaw and the others tried to isolate the special qualities that made strange attractors so enchanting. Sensitive dependence on initial conditions—the tendency of nearby trajectories to pull away from one another. This was the quality that made Lorenz realize that deterministic long-term weather forecasting was an impossibility. But where were the calipers to gauge such a quality? Could unpredictability itself be measured?

The answer to this question lay in a Russian conception, the Lyapunov exponent. This number provided a measure of just the topological qualities that corresponded to such concepts as unpredictability. The Lyapunov exponents in a system provided a way of measuring the conflicting effects of stretching, contracting, and folding in the phase space of an attractor. They gave a picture of all the properties of a system that lead to stability or instability. An exponent greater than zero meant stretching—nearby points would separate. An exponent smaller than zero meant contraction. For a fixed-point attractor, all the Lyapunov exponents were negative, since the direction of pull was inward toward the final steady state. An attractor in the form of a periodic orbit had one exponent of exactly zero and other exponents that were negative. A strange attractor, it turned out, had to have at least one positive Lyapunov exponent.

To their chagrin, the Santa Cruz students did not invent this idea, but they developed it in the most practical ways possible, learning how to measure Lyapunov exponents and relate them to other important properties. They used computer animation to make movies illustrating the beating together of order and chaos in dynamical systems. Their analysis showed vividly how some systems could create disorder in one direction while remaining trim and methodical in another. One movie showed what happened to a tiny cluster of nearby points—representing initial conditions—on a strange attractor as the system evolved in time. The cluster began to spread out and lose focus. It turned into a dot and then a blob. For certain kinds of attractors, the blob would quickly spread all over. Such attractors were efficient at mixing. For other attractors, though, the spreading would only occur in certain directions. The blob would become a band, chaotic along one axis and orderly along another. It was as if the system had an orderly impulse and a disorderly one together, and they were decoupling. As one impulse led to random unpredictability, the other kept time like a precise clock. Both impulses could be defined and measured.

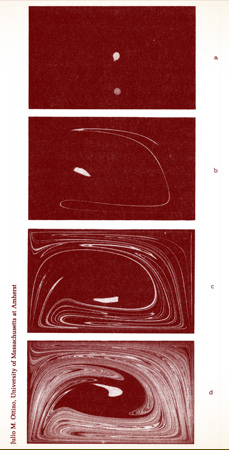
CHAOTIC MIXING. One blob mixes rapidly; another blob, just a bit closer to the center, barely mixes at all. In experiments by Julio M. Ottino and others with real fluids, the process of mixing—ubiquitous in nature and industry, yet still poorly understood—proved intimately bound up with the mathematics of chaos. The patterns revealed a stretching and folding that led back to the horseshoe map of Smale.

THE MOST CHARACTERISTICALLY Santa Cruzian imprint on chaos research involved a piece of mathematics cum philosophy known as information theory, invented in the late 1940s by a researcher at the Bell Telephone Laboratories, Claude Shannon. Shannon called his work “The Mathematical Theory of Communication,” but it concerned a rather special quantity called information, and the name information theory stuck. The theory was a product of the electronic age. Communication lines and radio transmissions were carrying a certain thing, and computers would soon be storing this same thing on punch cards or magnetic cylinders, and the thing was neither knowledge nor meaning. Its basic units were not ideas or concepts or even, necessarily, words or numbers. This thing could be sense or nonsense—but the engineers and mathematicians could measure it, transmit it, and test the transmission for accuracy. Information proved as good a word as any, but people had to remember that they were using a specialized value-free term without the usual connotations of facts, learning, wisdom, understanding, enlightenment.

Hardware determined the shape of the theory. Because information was stored in binary on-off switches newly designated as bits, bits became the basic measure of information. From a technical point of view, information theory became a handle for grasping how noise in the form of random errors interfered with the flow of bits. It gave a way of predicting the necessary carrying capacity of communication lines or compact disks or any technology that encoded language, sounds, or images. It offered a theoretical means of reckoning the effectiveness of different schemes for correcting errors—for example, using some bits as checks on others. It put teeth into the crucial notion of “redundancy.” In terms of Shannon’s information theory, ordinary language contains greater than fifty percent redundancy in the form of sounds or letters that are not strictly necessary to conveying a message. This is a familiar idea; ordinary communication in a world of mumblers and typographical errors depends on redundancy. The famous advertisement for shorthand training—if u cn rd ths msg…—illustrated the point, and information theory allowed it to be measured. Redundancy is a predictable departure from the random. Part of the redundancy in ordinary language lies in its meaning, and that part is hard to quantify, depending as it does on people’s shared knowledge of their language and the world. This is the part that allows people to solve crossword puzzles or fill in the missing word at the end of a. But other kinds of redundancy lend themselves more easily to numerical measures. Statistically, the likelihood that any letter in English will be “e” is far greater than one in twenty-six. Furthermore, letters do not have to be counted as isolated units. Knowing that one letter in an English text is “t” helps in predicting that the next might be “h” or “o,” and knowing two letters helps even more, and so on. The statistical tendency of various two- and three-letter combinations to turn up in a language goes a long way toward capturing some characteristic essence of the language. A computer guided only by the relative likelihood of the possible sequences of three letters can produce an otherwise random stream of nonsense that is recognizably English nonsense. Cryptologists have long made use of such statistical patterns in breaking simple codes. Communications engineers now use them in devising techniques to compress data, removing the redundancy to save space on a transmission line or storage disk. To Shannon, the right way to look at such patterns was this: a stream of data in ordinary language is less than random; each new bit is partly constrained by the bits before; thus each new bit carries somewhat less than a bit’s worth of real information. There was a hint of paradox floating in this formulation. The more random a data stream, the more information would be conveyed by each new bit.

Beyond its technical aptness to the beginning of the computer era, Shannon information theory gained a modest philosophical stature, and a surprising part of the theory’s appeal to people beyond Shannon’s field could be attributed to the choice of a single word: entropy. As Warren Weaver put it in a classic exposition of information theory, “When one meets the concept of entropy in communication theory, he has a right to be rather excited—a right to suspect that one has hold of something that may turn out to be basic and important.” The concept of entropy comes from thermodynamics, where it serves as an adjunct of the Second Law, the inexorable tendency of the universe, and any isolated system in it, to slide toward a state of increasing disorder. Divide a swimming pool in half with some barrier; fill one half with water and one with ink; wait for all to be still; lift the barrier; simply through the random motion of molecules, eventually the ink and water will mix. The mixing never reverses itself, even if you wait till the end of the universe, which is why the Second Law is so often said to be the part of physics that makes time a one-way street. Entropy is the name for the quality of systems that increases under the Second Law—mixing, disorder, randomness. The concept is easier to grasp intuitively than to measure in any real-life situation. What would be a reliable test for the level of mixing of two substances? One could imagine counting the molecules of each in some sample. But what if they were arranged yes-no-yes-no-yes-no-yes-no? Entropy could hardly be described as high. One could count just the even molecules, but what if the arrangement were yes-no-no-yes-yes-no-no-yes? Order intrudes in ways that defy any straightforward counting algorithm. And in information theory, issues of meaning and representation present extra complications. A sequence like 01 0100 0100 0010 111 010 11 00 000 0010 111 010 11 0100 0 000 000…might seem orderly only to an observer familiar with Morse code and Shakespeare. And what about the topologically perverse patterns of a strange attractor?

To Robert Shaw, strange attractors were engines of information. In his first and grandest conception, chaos offered a natural way of returning to the physical sciences, in reinvigorated form, the ideas that information theory had drawn from thermodynamics. Strange attractors, conflating order and disorder, gave a challenging twist to the question of measuring a system’s entropy. Strange attractors served as efficient mixers. They created unpredictability. They raised entropy. And as Shaw saw it, they created information where none existed.

Norman Packard was reading Scientific American one day and spotted an advertisement for an essay contest called the Louis Jacot competition. This was suitably far-fetched—a prize lucratively endowed by a French financier who had nurtured a private theory about the structure of the universe, galaxies within galaxies. It called for essays on Jacot’s theme, whatever that was. (“It sounded like a bunch of crank mail,” Farmer said.) But judging the competition was an impressive panel drawn from France’s scientific establishment, and the money was impressive as well. Packard showed the advertisement to Shaw. The deadline was New Year’s Day 1978.

By now the collective was meeting regularly in an outsized old Santa Cruz house not far from the beach. The house accumulated flea-market furniture and computer equipment, much of which was devoted to the roulette problem. Shaw kept a piano there, on which he would play baroque music or improvise his own blend of the classical and modern. In their meetings the physicists developed a working style, a routine of throwing out ideas and filtering them through some sieve of practicality, reading the literature, and conceiving papers of their own. Eventually they learned to collaborate on journal articles in a reasonably efficient round-robin way, but the first paper was Shaw’s, one of the few he would produce, and he kept the writing of it to himself, characteristically. Also characteristically, it was late.

In December 1977 Shaw headed out from Santa Cruz to attend the first meeting of the New York Academy of Sciences devoted to chaos. His superconductivity professor paid his fare, and Shaw arrived uninvited to hear in person the scientists he knew only from their writing. David Ruelle. Robert May. James Yorke. Shaw was awed by these men and also by the astronomical $35 room charge at the Barbizon Hotel. Listening to the talks, he swung back and forth between feeling that he had been ignorantly reinventing ideas that these men had worked out in considerable detail and, on the other hand, feeling that he had an important new point of view to contribute. He had brought the unfinished draft of his information theory paper, scribbled in longhand on scraps of paper in a folder, and he tried unsuccessfully to get a typewriter, first from the hotel and then from local repair shops. In the end he took his folder away with him. Later, when his friends begged him for details, he told them the high point had been a dinner in honor of Edward Lorenz, who was finally receiving the recognition that had eluded him for so many years. When Lorenz walked into the room, shyly holding his wife’s hand, the scientists rose to their feet to give him an ovation. Shaw was struck by how terrified the meteorologist looked.

A few weeks later, on a trip to Maine, where his parents had a vacation house, he finally mailed his paper to the Jacot competition. New Year’s had passed, but the envelope was generously backdated by the local postmaster. The paper—a blend of esoteric mathematics and speculative philosophy, illustrated with cartoon-like drawings by Shaw’s brother Chris—won an honorable mention. Shaw received a large enough cash prize to pay for a trip to Paris to collect the honor. It was a small enough achievement, but it came at a difficult moment in the group’s relations with the department. They desperately needed whatever external signs of credibility they could find. Farmer was giving up astrophysics, Packard was abandoning statistical mechanics, and Crutchfield still was not ready to call himself a graduate student. The department felt matters were out of control.

“STRANGE ATTRACTORS, CHAOTIC BEHAVIOR, and Information Flow” circulated that year in a preprint edition that eventually reached about 1,000, the first painstaking effort to weave together information theory and chaos.

Shaw brought some assumptions of classical mechanics out of the shadows. Energy in natural systems exists on two levels: the macroscales, where everyday objects can be counted and measured, and the microscales, where countless atoms swim in random motion, unmeasurable except as an average entity, temperature. As Shaw noted, the total energy living in the microscales could outweigh the energy of the macroscales, but in classical systems this thermal motion was irrelevant—isolated and unusable. The scales do not communicate with one another. “One does not have to know the temperature to do a classical mechanics problem,” he said. It was Shaw’s view, however, that chaotic and near-chaotic systems bridged the gap between macroscales and microscales. Chaos was the creation of information.

One could imagine water flowing past an obstruction. As every hydrodynamicist and white-water canoeist knows, if the water flows fast enough, it produces whorls downstream. At some speed, the whorls stay in place. At some higher speed, they move. An experimenter could choose a variety of methods for extracting data from such a system, with velocity probes and so forth, but why not try something simple: pick a point directly downstream from the obstruction and, at uniform time intervals, ask whether the whorl is to the right or the left.

If the whorls are static, the data stream will look like this: left-left-left-left-left-left-left-left-left-left-left-left-left-left-left-left-left-left-left-left-. After a while, the observer starts to feel that new bits of data are failing to offer new information about the system.

Or the whorls might be moving back and forth periodically: left-right-left-right-left-right-left-right-left-right-left-right-left-right-left-right-left-right-left-right-. Again, though at first the system seems one degree more interesting, it quickly ceases to offer any surprises.

As the system becomes chaotic, however, strictly by virtue of its unpredictability, it generates a steady stream of information. Each new observation is a new bit. This is a problem for the experimenter trying to characterize the system completely. “He could never leave the room,” as Shaw said. “The flow would be a continuous source of information.”

Where is this information coming from? The heat bath of the microscales, billions of molecules in their random thermodynamic dance. Just as turbulence transmits energy from large scales downward through chains of vortices to the dissipating small scales of viscosity, so information is transmitted back from the small scales to the large—at any rate, this was how Shaw and his colleagues began describing it. And the channel transmitting the information upward is the strange attractor, magnifying the initial randomness just as the Butterfly Effect magnifies small uncertainties into large-scale weather patterns.

The question was how much. Shaw found—after unwittingly duplicating some of their work—that again Soviet scientists had been there first. A. N. Kolmogorov and Yasha Sinai had worked out some illuminating mathematics for the way a system’s “entropy per unit time” applies to the geometric pictures of surfaces stretching and folding in phase space. The conceptual core of the technique was a matter of drawing some arbitrarily small box around some set of initial conditions, as one might draw a small square on the side of a balloon, then calculating the effect of various expansions or twists on the box. It might stretch in one direction, for example, while remaining narrow in the other. The change in area corresponded to an introduction of uncertainty about the system’s past, a gain or loss of information.

To the extent that information was just a fancy word for unpredictability, this conception merely matched the ideas that such scientists as Ruelle were developing. But the information theory framework allowed the Santa Cruz group to adopt a body of mathematical reasoning that had been well investigated by communications theorists. The problem of adding extrinsic noise to an otherwise deterministic system, for example, was new in dynamics but familiar enough in communications. The real appeal for these young scientists, however, was only partly the mathematics. When they spoke of systems generating information, they thought about the spontaneous generation of pattern in the world. “At the pinnacle of complicated dynamics are processes of biological evolution, or thought processes,” Packard said. “Intuitively there seems a clear sense in which these ultimately complicated systems are generating information. Billions of years ago there were just blobs of protoplasm; now billions of years later here we are. So information has been created and stored in our structure. In the development of one person’s mind from childhood, information is clearly not just accumulated but also generated—created from connections that were not there before.” It was the kind of talk that could make a sober physicist’s head spin.

THEY WERE TINKERERS FIRST, though, and philosophers only second. Could they make a bridge from the strange attractors they knew so well to the experiments of classical physics? It was one thing to say that right-left-right-right-left-right-left-left-left-right was unpredictable and information-generating. It was quite another to take a stream of real data and measure its Lyapunov exponent, its entropy, its dimension. Still, the Santa Cruz physicists had made themselves more comfortable with these ideas than had any of their older colleagues. By living with strange attractors day and night, they convinced themselves that they recognized them in the flapping, shaking, beating, swaying phenomena of their everyday lives.

They had a game they would play, sitting at a coffeehouse. They would ask: How far away is the nearest strange attractor? Was it that rattling automobile fender? That flag snapping erratically in a steady breeze? A fluttering leaf? “You don’t see something until you have the right metaphor to let you perceive it,” Shaw said, echoing Thomas S. Kuhn. Before long, their relativist friend Bill Burke was quite convinced that the speedometer in his car was rattling in the nonlinear fashion of a strange attractor. And Shaw, settling on an experimental project that would occupy him for years to come, adopted as homely a dynamical system as any physicist could imagine: a dripping faucet. Most people imagine the canonical dripping faucet as relentlessly periodic, but it is not necessarily so, as a moment of experimentation reveals. “It’s a simple example of a system that goes from predictable behavior to unpredictable behavior,” Shaw said. “If you turn it up a little bit, you can see a regime where the pitter-patter is irregular. As it turns out, it’s not a predictable pattern beyond a short time. So even something as simple as a faucet can generate a pattern that is eternally creative.”

As a generator of organization, the dripping faucet offers little to work with. It generates only drips, and each drip is about the same as the last. But for a beginning investigator of chaos, the dripping faucet proved to have certain advantages. Everyone already has a mental picture of it. The data stream is as one-dimensional as could be: a rhythmic drumbeat of single points measured in time. None of these qualities could be found in systems that the Santa Cruz group explored later—the human immune system, for example, or the troublesome beam-beam effect that was inexplicably degrading the performance of colliding particle beams at the Stanford Linear Accelerator Center to the north. Experimenters like Libchaber and Swinney obtained a one-dimensional data stream by placing a probe arbitrarily at one point in a slightly more complex system. In the dripping faucet the single line of data is all there is. And it isn’t even a continuously varying velocity or temperature—just a list of drip times.

Asked to organize an attack on such a system, a traditional physicist might begin by making as complete a physical model as possible. The processes governing the creation and breaking off of drips are understandable, if not quite so simple as they might seem. One important variable is the rate of flow. (This had to be slow compared to most hydrodynamic systems. Shaw usually looked at drop rates of 1 to 10 per second, which meant a flow rate of 30 to 300 gpf—gallons per fortnight.) Other variables include the viscosity of the fluid and the surface tension. A drop of water hanging from a faucet, waiting to break off, assumes a complicated three-dimensional shape, and the calculation of this shape alone was, as Shaw said, “a state-of-the-art computer calculation.” Furthermore, the shape is far from static. A drop filling with water is like a little elastic bag of surface tension, oscillating this way and that, gaining mass and stretching its walls until it passes a critical point and snaps off. A physicist trying to model the drip problem completely—writing down sets of coupled nonlinear partial differential equations with appropriate boundary conditions and then trying to solve them—would find himself lost in a deep, deep thicket.

An alternative approach would be to forget about the physics and look only at the data, as though it were coming out of a black box. Given a list of numbers representing intervals between drips, could an expert in chaotic dynamics find something useful to say? Indeed, as it turned out, methods could be devised for organizing such data and working backward into the physics, and these methods became critical to the applicability of chaos to real-world problems.

But Shaw began halfway between these extremes, by making a sort of caricature of a complete physical model. Ignoring drop shapes, ignoring complex motions in three dimensions, he roughly summarized drip physics. He imagined a weight hanging from a spring. He imagined that the weight grew steadily with time. As it grew, the spring would stretch and the weight would hang lower and lower. When it reached a certain point, a portion of the weight would break off. The amount that would detach, Shaw supposed arbitrarily, would depend strictly on the speed of the descending weight when it reached the cutoff point.

Then, of course, the remaining weight would bounce back up, as springs do, with oscillations that graduate students learn to model using standard equations. The interesting feature of the model—the only interesting feature, and the nonlinear twist that made chaotic behavior possible—was that the next drip depended on how the springiness interacted with the steadily increasing weight. A down bounce might help the weight reach the cutoff point that much sooner, or an up bounce might delay the process slightly. With a real faucet, drops are not all the same size. The size depends both on the velocity of the flow and on the direction of the bounce. If a drop starts off its life already moving downward, then it will break off sooner. If it happens to be on the rebound, it will be able to fill with a bit more water before it snaps. Shaw’s model was exactly crude enough to be summed up in three differential equations, the minimum necessary for chaos, as Poincaré and Lorenz had shown. But would it generate as much complexity as a real faucet? And would the complexity be of the same kind?

Thus Shaw found himself sitting in a laboratory in the physics building, a big plastic tub of water over his head, a tube running down to a premium-quality hardware-store brass nozzle. As each drop fell, it interrupted a light beam, and a microcomputer in the next room recorded the time. Meanwhile Shaw had his three arbitrary equations up and running on the analog computer, producing a stream of imaginary data. One day he performed some show-and-tell for the faculty—a “pseudocolloquium,” as Crutch-field said, because graduate students were not permitted to give formal colloquiums. Shaw played a tape of a faucet making its drumbeat on a piece of tin. And he had his computer going click-click-click in a crisp syncopation, revealing patterns to the ear. He had solved the problem simultaneously from front and back, and his listeners could hear the deep structure in this seemingly disorderly system. But to go further, the group needed a way of taking raw data from any experiment and working backward to equations and strange attractors that characterized chaos.

With a more complicated system, one could imagine plotting one variable against another, relating changes in temperature or velocity to the passage of time. But the dripping faucet provided only a series of times. So Shaw tried a technique that may have been the Santa Cruz group’s cleverest and most enduring practical contribution to the progress of chaos. It was a method of reconstructing a phase space for an unseen strange attractor, and it could be applied to any series of data at all. For the dripping faucet data, Shaw made a two-dimensional graph in which the x axis represented a time interval between a pair of drops and the y axis represented the next time interval. If 150 milliseconds passed between drop one and drop two, and then 150 milliseconds passed between drop two and drop three, he would plot a point at the position 150-150.

That was all there was to it. If the dripping was regular, as it tended to be when the water flowed slowly and the system was in its “water clock regime,” the graph would be suitably dull. Every point would land at the same place. The graph would be a single dot. Or almost. Actually, the first difference between the computer dripping faucet and the real dripping faucet was that the real version was subject to noise, and exceedingly sensitive. “It turns out that the thing is an excellent seismometer,” Shaw said ironically, “very efficient in bringing noise up from the little-league scales to the big-league scales.” Shaw ended up doing most of his work at night, when foot traffic in the physics corridors was lightest. Noise meant that, instead of the single dot predicted by theory, he would see a slightly fuzzy blob.

As the flow rate was increased, the system would go through a period-doubling bifurcation. Drops would fall in pairs. One interval might be 150 milliseconds, and the next might be 80. So the graph would show two fuzzy blobs, one centered at 150-80 and the other at 80-150. The real test came when the pattern became chaotic. If it were truly random, points would be scattered all over the graph. There would be no relation to be found between one interval and the next. But if a strange attractor were hidden in the data, it might reveal itself as a coalescence of fuzziness into distinguishable structures.

Often three dimensions were necessary to see the structure, but that was no problem. The technique could easily be generalized to higher-dimensional graph-making. Instead of plotting interval n against interval n +1, one could plot interval n against interval n + 1 against interval n + 2. It was a trick—a gimmick. Ordinarily a three-dimensional graph required knowledge of three independent variables in a system. The trick gave three variables for the price of one. It reflected the faith of these scientists that order was so deeply ingrained in apparent disorder that it would find a way of expressing itself even to experimenters who did not know which physical variables to measure or who were not able to measure such variables directly. As Farmer said, “When you think about a variable, the evolution of it must be influenced by whatever other variables it’s interacting with. Their values must somehow be contained in the history of that thing. Somehow their mark must be there.” In the case of Shaw’s dripping faucet the pictures illustrated the point. In three dimensions, especially, the patterns emerged, resembling loopy trails of smoke left by an out-of-control sky-writing plane. Shaw was able to match plots of the experimental data with data produced by his analog computer model, the main difference being that the real data was always fuzzier, smeared out by noise. Even so, the structure was unmistakable. The Santa Cruz group began collaborating with such experienced experimentalists as Harry Swinney, who had moved to the University of Texas in Austin, and they learned how to retrieve strange attractors from all kinds of systems. It was a matter of embedding the data in a phase space of enough dimensions. Soon Floris Takens, who had invented strange attractors with David Ruelle, independently gave a mathematical foundation for this powerful technique of reconstructing the phase space of an attractor from a stream of real data. As countless researchers soon discovered, the technique distinguishes between mere noise and chaos, in the new sense: orderly disorder created by simple processes. Truly random data remains spread out in an undefined mess. But chaos—deterministic and patterned—pulls the data into visible shapes. Of all the possible pathways of disorder, nature favors just a few.

THE TRANSITION FROM REBEL to physicist was slow. Every so often, sitting in a coffeehouse or working in their laboratory, one or another of the students would have to fight back amazement that their scientific fantasy had not ended. God, we’re still doing this and it still makes sense, as Jim Crutchfield would say. We’re still here. How far is it going to go?

Their chief supporters on the faculty were the Smale protégé Ralph Abraham in the mathematics department and in the physics department Bill Burke, who had himself made “czar of the analog computer” to protect the collective’s claim to this piece of equipment, at least. The rest of the physics faculty found itself in a more difficult position. A few years later, some professors denied bitterly that the collective had been forced to overcome indifference or opposition from the department. The collective reacted just as bitterly to what it considered revisionist history on the part of belated converts to chaos. “We had no advisor, nobody telling us what to do,” said Shaw. “We were in an adversary role for years, and it continues to this day. We were never funded at Santa Cruz. Every one of us worked for considerable periods of time without pay, and it was a shoestring operation the entire way, with no intellectual or other guidance.”

By its lights, though, the faculty tolerated and even abetted a long period of research that seemed to fall short of any substantial kind of science. Shaw’s thesis advisor in superconductivity kept him on salary for a year or so, long after Shaw had veered away from low-temperature physics. No one ever quite ordered the chaos research to stop. At worst the faculty reached an attitude of benevolent discouragement. Each member of the collective was taken aside from time to time for heart-to-heart talks. They were warned that, even if somehow a way could be found to justify doctorates, no one would be able to help the students find jobs in a nonexistent field. This may be a fad, the faculty would say, and then where will you be? Yet outside the redwood shelter of the Santa Cruz hills, chaos was creating its own scientific establishment, and the Dynamical Systems Collective had to join it.

One year Mitchell Feigenbaum came by, making the rounds of the lecture circuit to explain his breakthrough in universality. As always, his talks were abstrusely mathematical; renormalization group theory was an esoteric piece of condensed matter physics that these students had not studied. Besides, the collective was more interested in real systems than in delicate one-dimensional maps. Doyne Farmer, meanwhile, heard that a Berkeley mathematician, Oscar E. Lanford III, was exploring chaos, and he went up to talk. Lanford listened politely and then looked at Farmer and said they had nothing in common. He was trying to understand Feigenbaum.

How deadly! Where’s the guy’s sense of scope? Farmer thought. “He was looking at these little orbits. Meanwhile we were into information theory with all its profundity, taking chaos apart, seeing what make it tick, trying to relate metric entropy and Lya-punov exponents to more statistical measures.”

In his conversation with Farmer, Lanford did not emphasize universality, and only later did Farmer realize that he had missed the point. “It was my naïveté,” Farmer said. “The idea of universality was not just a great result. Mitchell’s thing was also a technique to employ a whole army of unemployed critical phenomena people.

“Up to that point it appeared that nonlinear systems would have to be treated in a case-by-case way. We were trying to come up with a language to quantify it and describe it, but it still seemed as though everything would have to be treated case by case. We saw no way to put systems in classes and write solutions that would be valid for the whole class, as in linear systems. Universality meant finding properties that were exactly the same in quantifiable ways for everything in that class. Predictable properties. That’s why it was really important.

“And there was a sociological factor that pumped even more fuel. Mitchell cast his results in the language of renormalization. He took all this machinery that people in critical phenomena had been skilled in using. Those guys were having a hard time, because there didn’t seem to be any interesting problems left for them to do. They were looking around for something else to apply their bag of tricks to. And suddenlyFeigenbaum came forward with his extremely significant application of this bag of tricks. It spawned an entire subdiscipline.”

Quite independently, however, the Santa Cruz students began to make an impression of their own. Within the department their star began to rise after a surprise appearance at a midwinter meeting in condensed matter physics in Laguna Beach in 1978, organized by Bernardo Huberman of the Xerox Palo Alto Research Center and Stanford University. The collective was not invited, but it went nonetheless, bundling itself into Shaw’s 1959 Ford ranch-style station wagon, an automobile known as the Cream Dream. Just in case, the group brought some equipment, including a huge television monitor and a videotape. When an invited speaker canceled at the last minute, Huberman invited Shaw to take his place. The timing was perfect. Chaos had attained the status of buzzword, but few of the physicists attending the conference knew what it meant. So Shaw began by explaining attractors in phase space: first fixed points (where everything stops); then limit cycles (where everything oscillates); then strange attractors (everything else). He demonstrated with his computer graphics on videotape. (“Audiovisual aids gave us an edge,” he said. “We could hypnotize them with flashing lights.”) He illuminated the Lorenz attractor and the dripping faucet. He explained the geometry—how shapes are stretched and folded, and what that meant in the grand terms of information theory. And for good measure, he put in a few words at the end about shifting paradigms. The talk was a popular triumph, and in the audience were several members of the Santa Cruz faculty, seeing chaos for the first time through the eyes of their colleagues.

IN 1979 THE WHOLE GROUP attended the second chaos meeting of the New York Academy of Sciences, this time as participants, and now the field was exploding. The 1977 meeting had been Lorenz’s, attended by specialists numbering in the dozens. This meeting was Feigenbaum’s, and scientists came by the hundreds. Where two years earlier Rob Shaw had shyly tried to find a typewriter so that he could produce a paper to leave under people’s doors, now the Dynamical Systems Collective had become a virtual printing press, producing papers rapidly and always under joint authorship.

But the collective could not go on forever. The closer it came to the real world of science, the closer it came to unraveling. One day Bernardo Huberman called. He asked for Rob Shaw, but he happened to get Crutchfield. Huberman needed a collaborator for a tight, simple paper about chaos. Crutchfield, the youngest member of the collective, concerned about being thought of as merely its “hacker,” was beginning to realize that in one respect the Santa Cruz faculty had been right all along: each of the students was someday going to have to be judged as an individual. Huberman, furthermore, had all the sophistication about the profession of physics that the students lacked, and in particular he knew how to get the most mileage from a given piece of work. He had his doubts, having seen their laboratory—“It was all very vague, you know, sofas and bean bags, like stepping into a time machine, flower children and the 1960s again.” But he needed an analog computer, and in fact Crutchfield managed to get his research program running in hours. The collective was a problem, though. “All the guys want in,” Crutchfield said at one point, and Huberman said absolutely not. “It’s not just the credit, it’s the blame. Suppose the paper is wrong—you’re going to blame a collective? I’m not part of a collective.” He wanted one partner for a clean job.

The result was just what Huberman had hoped for: the first paper about chaos to be published in the premier American journal for reporting breakthroughs in physics, Physical Review Letters. In terms of scientific politics this was a nontrivial achievement. “To us it was fairly obvious stuff,” Crutchfield said, “but what Bernardo understood was that it would have a huge impact.” It was also one beginning of the group’s assimilation into the real world. Farmer was angered, seeing in Crutchfielďs defection an undermining of the collective spirit.

Crutchfield was not alone in stepping outside the group. Soon Farmer himself, and Packard, too, were collaborating with established physicists and mathematicians: Huberman, Swinney, Yorke. The ideas formed in the cauldron at Santa Cruz became a firm part of the framework of the modern study of dynamical systems. When a physicist with a mass of data wanted to investigate its dimension or its entropy, the appropriate definitions and working techniques might well be those created in the years of patching plugs in the Systron-Donner analog computer and staring at the oscilloscope. Climate specialists would argue about whether the chaos of the world’s atmosphere and oceans had infinite dimensions, as traditional dynamicists would assume, or somehow followed a low-dimensional strange attractor. Economists analyzing stock market data would try to find attractors of dimension 3.7 or 5.3. The lower the dimension, the simpler the system. Many mathematical peculiarities had to be sorted and understood. Fractal dimension, Hausdorff dimension, Lyapunov dimension, information dimension—the subtleties of these measures of a chaotic system were best explained by Farmer and Yorke. An attractor’s dimension was “the first level of knowledge necessary to characterize its properties.” It was the feature that gave “the amount of information necessary to specify the position of a point on the attractor to within a given accuracy.” The methods of the Santa Cruz students and their older collaborators tied these ideas to the other important measures of systems: the rate of decay of predictability, the rate of information flow, the tendency to create mixing. Sometimes scientists using these methods would find themselves plotting data, drawing little boxes, and counting the number of data points in each box. Yet even such seemingly crude techniques brought chaotic systems for the first time within the reach of scientific understanding.

Meanwhile, having learned to look for strange attractors in flapping flags and rattling speedometers, the scientists made a point of finding the symptoms of deterministic chaos all through the current literature of physics. Unexplained noise, surprising fluctuations, regularity mixing with irregularity—these effects popped up in papers from experimentalists working with everything from particle accelerators to lasers to Josephson junctions. The chaos specialists would make these symptoms their own, telling the unconverted, in effect, your problems are our problems. “Several experiments on Josephson junction oscillators have revealed a striking noise-rise phenomena,” a paper would begin, “which cannot be accounted for in terms of thermal fluctuations.”

By the time the collective departed, some of the Santa Cruz faculty had turned to chaos, too. Other physicists, though, felt in retrospect that Santa Cruz had missed an opportunity to begin the kind of national center for work in nonlinear dynamics that soon began appearing on other campuses. In the early 1980s the members of the collective graduated and dispersed. Shaw finished his dissertation in 1980, Farmer in 1981, Packard in 1982. Crutchfield’s appeared in 1983, a typographical hodgepodge interleaving typed pages with no less than eleven papers already published in the journals of physics and mathematics. He went on to the University of California at Berkeley. Farmer joined the Theoretical Division of Los Alamos. Packard and Shaw joined the Institute for Advanced Study in Princeton. Crutchfield studied video feedback loops. Farmer worked on “fat fractals” and modeled the complex dynamics of the human immune system. Packard explored spatial chaos and the formation of snowflakes. Only Shaw seemed reluctant to join the mainstream. His own influential legacy comprised just two papers, one that had won him a trip to Paris and one, about the dripping faucet, that summed up all his Santa Cruz research. Several times, he came close to quitting science altogether. As one of his friends said, he was oscillating.