The Elegant Universe: Superstrings, Hidden Dimensions, and the Quest for the Ultimate Theory - Brian Greene (2010)
Part IV. String Theory and the Fabric of Spacetime
Chapter 13. Black Holes: A String/M-Theory Perspective
The pre-string theory conflict between general relativity and quantum mechanics was an affront to our visceral sense that the laws of nature should fit together in a seamless, coherent whole. But this antagonism was more than a towering abstract disjunction. The extreme physical conditions that occurred at the moment of the big bang and that prevail within black holes cannot be understood without a quantum mechanical formulation of the gravitational force. With the discovery of string theory, we now have a hope of solving these deep mysteries. In this and the next chapter, we describe how far string theorists have gone toward understanding black holes and the origin of the universe.
Black Holes and Elementary Particles
At first sight it's hard to imagine any two things more radically different than black holes and elementary particles. We usually picture black holes as the most gargantuan of heavenly bodies, whereas elementary particles are the most minute specks of matter. But the research of a number of physicists during the late 1960s and early 1970s, including Demetrios Christodoulou, Werner Israel, Richard Price, Brandon Carter, Roy Kerr, David Robinson, Hawking, and Penrose, showed that black holes and elementary particles are perhaps not as different as one might think. These physicists found increasingly persuasive evidence for what John Wheeler has summarized by the statement "black holes have no hair." By this, Wheeler meant that except for a small number of distinguishing features, all black holes appear to be alike. The distinguishing features? One, of course, is the black hole's mass. What are the others? Research has revealed that they are the electric and certain other force charges a black hole can carry, as well as the rate at which it spins. And that's it. Any two black holes with the same mass, force charges, and spin are completely identical. Black holes do not have fancy "hairdos"—that is, other intrinsic traits—that distinguish one from another. This should ring a loud bell. Recall that it is precisely such properties—mass, force charges, and spin—that distinguish one elementary particle from another. The similarity of the defining traits has led a number of physicists over the years to the strange speculation that black holes might actually be gigantic elementary particles.
In fact, according to Einstein's theory, there is no minimum mass for a black hole. If we crush a chunk of matter of any mass to a small enough size, a straightforward application of general relativity shows that it will become a black hole. (The lighter the mass, the smaller we must crush it.) And so, we can imagine a thought experiment in which we start with ever-lighter blobs of matter, crush them into ever-smaller black holes, and compare the properties of the resulting black holes with the properties of elementary particles. Wheeler's no-hair statement leads us to conclude that for small enough masses the black holes we form in this manner will look very much like elementary particles. Both will look like tiny bundles characterized completely by their mass, force charges, and spin.
But there is a catch. Astrophysical black holes, with masses many times that of the sun, are so large and heavy that quantum mechanics is largely irrelevant and only the equations of general relativity need be used to understand their properties. (We are here discussing the overall structure of the black hole, not the singular central point of collapse within a black hole, whose tiny size most certainly requires a quantum-mechanical description.) As we try to make ever less massive black holes, however, there comes a point when they are so light and small that quantum mechanics does comes into play. This happens if the total mass of the black hole is about the Planck mass or less. (From the point of view of elementary particle physics, the Planck mass is huge—some ten billion billion times the mass of a proton. From the point of view of black holes, though, the Planck mass, being equal to that of an average grain of dust, is quite tiny.) And so, physicists who speculated that tiny black holes and elementary particles might be closely related immediately ran up against the incompatibility between general relativity—the theoretical heart of black holes—and quantum mechanics. In the past, the incompatibility stymied all progress in this intriguing direction.
Does String Theory Allow Us to Go Forward?
It does. Through a fairly unexpected and sophisticated realization of black holes, string theory provides the first theoretically sound connection between black holes and elementary particles. The road to this connection is a bit circuitous, but it takes us through some of the most interesting developments in string theory, making it a journey well worth taking.
It begins with a seemingly unrelated question that string theorists have kicked around since the late 1980s. Mathematicians and physicists have long known that when six spatial dimensions are curled up into a Calabi-Yau shape, there are generally two kinds of spheres that are embedded within the shape's fabric. One kind are the two-dimensional spheres, like the surface of a beach ball, that played a vital role in the space-tearing flop transitions of Chapter 11. The other kind are harder to picture but they are equally prevalent. They are three-dimensional spheres—like the surfaces of beach balls adorning the sandy ocean shores of a universe with four extended space dimensions. Of course, as we discussed in Chapter 11, an ordinary beach ball in our world is itself a three-dimensional object, but its surface, just like the surface of a garden hose, is two-dimensional: You need only two numbers—latitude and longitude, for instance—to locate any position on its surface. But we are now imagining having one more space dimension: a four-dimensional beach ball whose surface is three-dimensional. As it's pretty close to impossible to picture such a beach ball in your mind's eye, for the most part we will appeal to lower-dimensional analogs that are more easily visualized. But, as we shall now see, one aspect of the three-dimensional nature of the spherical surfaces is of prime importance.
By studying the equations of string theory, physicists realized that it is possible, and even likely, that as time evolves, these three-dimensional spheres will shrink—collapse—to vanishingly small volume. But what would happen, string theorists asked, if the fabric of space were to collapse in this manner? Will there be some catastrophic effect from this kind of pinching of the spatial fabric? This is much like the question we posed and resolved in Chapter 11, but here we are focusing on collapsing three-dimensional spheres, whereas in Chapter 11 we focused solely on collapsing two-dimensional spheres. (As in Chapter 11, since we are envisioning that a piece of a Calabi-Yau shape is shrinking, as opposed to the whole Calabi-Yau shape itself, the small radius/large radius identification of Chapter 10 does not apply.) Here is the essential qualitative difference arising from the change in dimension.1 We recall from Chapter 11 that a pivotal realization is that strings, as they move through space, can lasso a two-dimensional sphere. That is, their two-dimensional world-sheet can fully surround a two-dimensional sphere, as in Figure 11.6. This proves to be just enough protection to keep a collapsing, pinching two-dimensional sphere from causing physical catastrophes. But now we are looking at the other kind of sphere inside a Calabi-Yau space, and it has too many dimensions for it to be surrounded by a moving string. If you have trouble seeing this, it is perfectly okay to think of the analogy obtained by lowering all dimensions by one. You can picture three-dimensional spheres as if they are two-dimensional surfaces of ordinary beach balls, so long as you also picture one-dimensional strings as if they are zero-dimensional point particles. Then, in analogy with the fact that a zero-dimensional point-particle cannot lasso anything, let alone a two-dimensional sphere, a one-dimensional string cannot lasso a three-dimensional sphere.
Such reasoning led string theorists to speculate that if a three-dimensional sphere inside a Calabi-Yau space were to collapse, something that the approximate equations showed to be a perfectly possible if not commonplace evolution in string theory, it might yield a cataclysmic result. In fact, the approximate equations of string theory developed prior to the mid-1990s seemed to indicate that the workings of the universe would grind to a halt if such a collapse were to occur; they indicated that certain of the infinities tamed by string theory would be unleashed by such a pinching of the spatial fabric. For a number of years, string theorists had to live with this disturbing, albeit inconclusive, state of understanding. But in 1995, Andrew Strominger showed that these doomsaying speculations were wrong.
Strominger, following earlier groundbreaking work of Witten and Seiberg, made use of the realization that string theory, when analyzed with the newfound precision of the second superstring revolution, is not just a theory of one-dimensional strings. He reasoned as follows. A one-dimensional string—a one-brane in the newer language of the field—can completely surround a one-dimensional piece of space, like a circle, as we illustrate in Figure 13.1. (Notice that this is different from Figure 11.6, in which a one-dimensional string, as it moves through time, lassos a two-dimensional sphere. Figure 13.1 should be viewed as a snapshot taken at one instant in time.) Similarly, in Figure 13.1 we see that a two-dimensional membrane—a two-brane—can wrap around and completely cover a two-dimensional sphere, much as a piece of plastic wrap can be tightly wrapped around the surface of an orange. Although it's harder to visualize, Strominger followed the pattern and realized that the newly discovered three-dimensional ingredients in string theory—the three-branes—can wrap around and completely cover a three-dimensional sphere. Having seen clear to this insight, Strominger then showed, with a simple and standard physics calculation, that the wrapped three-brane provides a tailor-made shield that exactly cancels all of the potentially cataclysmic effects that string theorists had previously feared would occur if a three-dimensional sphere were to collapse.
This was a wonderful and important insight. But its full power was not revealed until a short time later.
Figure 13.1 A string can encircle a one-dimensional curled-up piece of the spatial fabric; a two-dimensional membrane can wrap around a two-dimensional piece.
Tearing the Fabric of Space—with Conviction
One of the most exciting things about physics is how the state of knowledge can change literally overnight. The morning after Strominger posted his paper on the electronic Internet archive, I read it in my office at Cornell after having retrieved it from the World Wide Web. In one stroke, Strominger had made use of the exciting new insights of string theory to resolve one of the thorniest issues surrounding the curling up of extra dimensions into a Calabi-Yau space. But as I pondered his paper, it struck me that he might have worked out only half of the story.
In the earlier space-tearing flop-transition work described in Chapter 11, we had studied a two-part process in which a two-dimensional sphere pinches down to a point, causing the fabric of space to tear, and then the two-dimensional sphere reinflates in a new way, thereby repairing the tear. In Strominger's paper, he had studied what happens when a three-dimensional sphere pinches down to a point, and had shown that the newfound extended objects in string theory ensure that physics continues to be perfectly well behaved. But that's where his paper stopped. Might it be that there was another half to the story, involving, once again, the tearing of space and its subsequent repair through the reinflation of spheres?
Dave Morrison was visiting me at Cornell during the spring term of 1995, and that afternoon we got together to discuss Strominger's paper. Within a couple of hours we had an outline of what the "second half of the story" might look like. Drawing on some insights from the late 1980s of the mathematicians Herb Clemens of the University of Utah, Robert Friedman of Columbia University, and Miles Reid of the University of Warwick, as applied by Candelas, Green, and Tristan Hübsch, then of the University of Texas at Austin, we realized that when a three-dimensional sphere collapses, it may be possible for the Calabi-Yau space to tear and subsequently repair itself by reinflating the sphere. But there is an important surprise. Whereas the sphere that collapsed had three dimensions, the one that reinflates has only two. It's hard to picture what this looks like, but we can get an idea by focusing on a lower-dimensional analogy. Rather than the hard-to-picture case of a three-dimensional sphere collapsing and being replaced by a two-dimensional sphere, let's imagine a one- dimensional sphere collapsing and being replaced by a zero-dimensional sphere.
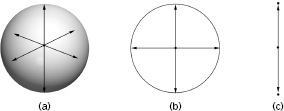
Figure 13.2 Spheres of dimensions that can be easily visualized—those of (a) two, (b) one, and (c) zero dimensions.
First of all, what are one-and zero-dimensional spheres? Well, let's reason by analogy. A two-dimensional sphere is the collection of points in three-dimensional space that are the same distance from a chosen center, as shown in Figure 13.2(a). By following the same idea, a one-dimensional sphere is the collection of points in two-dimensional space (the surface of this page, for example) that are the same distance from a chosen center. As shown in Figure 13.2(b), this is nothing but a circle. Finally, following the pattern, a zero-dimensional sphere is the collection of points in a one-dimensional space (a line) that are the same distance from a chosen center. As shown in Figure 13.2(c), this amounts to two points, with the "radius" of the zero-dimensional sphere equal to the distance each point is from their common center. And so, the lower-dimensional analogy alluded to in the preceding paragraph involves a circle (a one-dimensional sphere) pinching down, followed by space tearing, and then being replaced by a zero-dimensional sphere (two points). Figure 13.3 puts this abstract idea into practice.
We imagine beginning with the surface of a doughnut, in which a one-dimensional sphere (a circle) is embedded, as highlighted in Figure 13.3. Now, let's imagine that as time goes by, the highlighted circle collapses, causing the fabric of space to pinch. We can repair the pinch by allowing the fabric to momentarily tear, and then replacing the pinched one-dimensional sphere—the collapsed circle—with a zero-dimensional sphere—two points—plugging the holes in the upper and lower portions of the shape arising from the tear. As shown in Figure 13.3, the resulting shape looks like a warped banana, which through gentle deformation (non-space tearing) can be reshaped smoothly into the surface of a beach ball. We see, therefore, that when a one-dimensional sphere collapses and is replaced by a zero-dimensional sphere, the topology of the original doughnut, that is, its fundamental shape, is drastically altered. In the context of the curled-up spatial dimensions, the space-tearing progression of Figure 13.3 would result in the universe depicted in Figure 8.8 evolving into that depicted in Figure 8.7.
![]()
Figure 13.3 A circular piece of a doughnut (a torus) collapses to a point. The surface tears open, yielding two puncture holes. A zero-dimensional sphere (two points) is "glued in," replacing the original one-dimensional sphere (the circle) and repairing the torn surface. This allows a transformation to a completely different shape—a beach ball.
Although this is a lower-dimensional analogy, it captures the essential features of what Morrison and I foresaw for the second half of Strominger's story. After the collapse of a three-dimensional sphere inside a Calabi-Yau space, it seemed to us that space could tear and subsequently repair itself by growing a two-dimensional sphere, leading to far more drastic changes in topology than Witten and we had found in our earlier work (discussed in Chapter 11). In this way, one Calabi-Yau shape could, in essence, transform itself into a completely different Calabi-Yau shape—much like the doughnut transforming into the beach ball in Figure 13.3—while string physics remained perfectly well behaved. Although a picture was starting to emerge, we knew that there were significant aspects that we would need to work out before we could establish that our second half of the story did not introduce any singularities—that is, pernicious and physically unacceptable consequences. We each went home that evening with the tentative elation that we were sitting on a major new insight.
A Flurry of E-Mail
The next morning I received an e-mail from Strominger asking me for any comments or reactions to his paper. He mentioned that "it should tie in somehow with your work with Aspinwall and Morrison," because, as it turned out, he too had been exploring a possible connection to the phenomenon of topology change. I immediately sent him an e-mail describing the rough outline Morrison and I had come up with. When he responded, it was clear that his level of excitement matched what Morrison and I had been riding since the preceding day.
During the next few days a continuous stream of e-mail messages circulated between the three of us as we sought feverishly to put quantitative rigor behind our idea of drastic space-tearing topology change. Slowly but surely, all the details fell into place. By the following Wednesday, a week after Strominger posted his initial insight, we had a draft of a joint paper spelling out the dramatic new transformation of the spatial fabric that can follow the collapse of a three-dimensional sphere.
Strominger was scheduled to give a seminar at Harvard the next day, and so left Santa Barbara in the early morning. We agreed that Morrison and I would continue to fine-tune the paper and then submit it to the electronic archive that evening. By 11:45 P.M., we had checked and rechecked our calculations and everything seemed to hang together perfectly. And so, we electronically submitted our paper and headed out of the physics building. As Morrison and I walked toward my car (I was going to drive him to the house he had rented for the term) our discussion turned to one of devil's advocacy, in which we imagined the harshest criticisms that someone determined not to accept our results might level. As we drove out of the parking lot and left the campus, we realized that although our arguments were strong and convincing, they were not thoroughly airtight. Neither of us felt that there was any real chance that our work was wrong, but we did recognize that the strength of our claims and the particular wording we had chosen at a few points in the paper might leave the ideas open to rancorous debate, potentially obscuring the importance of the results. We agreed that it might have been better had we written the paper in a somewhat lower key, underplaying the depth of the claims, and allowing the physics community to judge the paper on its merits, rather than possibly reacting to the form of its presentation.
As we drove on, Morrison reminded me that under the rules of the electronic archive we could revise our paper until 2 A.M., when it would then be released for public Internet access. I immediately turned the car around and we drove back to the physics building, retrieved our initial submission, and set to work on toning down the prose. Thankfully, it was quite easy to do. A few word changes in critical paragraphs softened the edge of our claims without compromising the technical content. Within an hour, we resubmitted the paper, and agreed not to talk about it at all during the drive to Morrison's house.
By early the next afternoon it was evident that the response to our paper was enthusiastic. Among the many e-mail responses was one from Plesser, who gave us one of the highest compliments one physicist can give another by declaring, "I wish that I had thought of that!" Notwithstanding our fears the previous night, we had convinced the string theory community that not only can the fabric of space undergo the mild tears discovered earlier (Chapter 11), but that far more drastic rips, roughly illustrated by Figure 13.3, can occur as well.
Returning to Black Holes and Elementary Particles
What does this have to do with black holes and elementary particles? A lot. To see this, we must ask ourselves the same question we posed in Chapter 11. What are the observable physical consequences of such tears in the fabric of space? For flop transitions, as we have seen, the surprising answer to this question was that not much happens at all. For conifold transitions—the technical name for the drastic space-tearing transitions we had now found—there is, once again, no physical catastrophe (as there would be in conventional general relativity), but there are more pronounced observable consequences.
Two related notions underlie these observable consequences; we will explain each in turn. First, as we have discussed, Strominger's initial breakthrough was his realization that a three-dimensional sphere inside a Calabi-Yau space can collapse without an ensuing disaster, because a three-brane wrapped around it provides a perfect protective shield. But what does such a wrapped-brane configuration look like? The answer comes from earlier work of Horowitz and Strominger, which showed that to persons such as ourselves who are directly cognizant only of the three extended spatial dimensions, the three-brane "smeared" around the three-dimensional sphere will set up a gravitational field that looks like that of a black hole.2 This is not obvious and becomes clear only from a detailed study of the equations governing the branes. Again, it's hard to draw such higher-dimensional configurations accurately on a page, but Figure 13.4 conveys the rough idea with a lower-dimensional analogy involving two-dimensional spheres. We see that a two-dimensional membrane can smear itself around a two-dimensional sphere (which itself is sitting inside a Calabi-Yau space positioned at some location in the extended dimensions). Someone looking through the extended dimensions toward this location will sense the wrapped brane by its mass and the force charges it carries, properties that Horowitz and Strominger had shown would look just like those of a black hole. Moreover, in Strominger's 1995 breakthrough paper, he argued that the mass of the three-brane—the mass of the black hole, that is—is proportional to the volume of the three-dimensional sphere it wraps: The bigger the volume of the sphere, the bigger the three-brane must be in order to wrap around it, and the more massive it becomes. Similarly, the smaller the volume of the sphere, the smaller the mass of the three-brane that wraps it. As this sphere collapses, then, a three-brane that wraps around the sphere, which is perceived as a black hole, appears to become ever lighter. When the three-dimensional sphere has collapsed to a pinched point, the corresponding black hole—brace yourself—is massless. Although it sounds completely mysterious—what in the world is a massless black hole?—we will soon connect this enigma with more familiar string physics.

Figure 13.4 When a brane wraps around a sphere that is within the curled-up dimensions, it appears as a black hole in the familiar extended dimensions.
The second ingredient we need to recall is that the number of holes in a Calabi-Yau shape, as discussed in Chapter 9, determines the number of low-energy, and hence low-mass, vibrational string patterns, the patterns that can possibly account for the particles in Table 1.1 as well as the force carriers. Since the space-tearing conifold transitions change the number of holes (as, for example in Figure 13.3, in which the hole of the doughnut is eliminated by the tearing/repairing process), we expect a change in the number of low-mass vibrational patterns. Indeed, when Morrison, Strominger, and I studied this in detail, we found that as a new two-dimensional sphere replaces the pinched three-dimensional sphere in the curled-up Calabi-Yau dimensions, the number of massless string vibrational patterns increases by exactly one. (The example of the doughnut turning into a beach ball in Figure 13.3 would lead you to believe that the number of holes—and thus the number of patterns—decreases, but this proves to be a misleading property of the lower-dimensional analogy.)
To combine the observations of the preceding two paragraphs, imagine a sequence of snapshots of a Calabi-Yau space in which the size of a particular three-dimensional sphere gets smaller and smaller. The first observation implies that a three-brane wrapping around this three-dimensional sphere—which appears to us as a black hole—will have ever smaller mass until, at the final point of collapse, it will be massless. But, as we asked above, what does this mean? The answer became clear to us by invoking the second observation. Our work showed that the new massless pattern of string vibration arising from the space-tearing conifold transition is the microscopic description of a massless particle into which the black hole has transmuted. We concluded that as a Calabi-Yau shape goes through a space-tearing conifold transition, an initially massive black hole becomes ever lighter until it is massless and then it transmutes into a massless particle—such as a massless photon—which in string theory is nothing but a single string executing a particular vibrational pattern. In this way, for the first time, string theory explicitly establishes a direct, concrete, and quantitatively unassailable connection between black holes and elementary particles.
"Melting" Black Holes
The connection between black holes and elementary particles which we found is closely akin to something we are all familiar with from day-to-day life, known technically as a phase transition. A simple example of a phase transition is the one we mentioned in the last chapter: water can exist as a solid (ice), as a liquid (liquid water), and a gas (steam). These are known as the phases of water, and the transformation from one form to another is called a phase transition. Morrison, Strominger, and I showed that there is a tight mathematical and physical analogy between such phase transitions and the space-tearing conifold transitions from one Calabi-Yau shape to another. Again, just as someone who has never before encountered liquid water or solid ice would not immediately recognize that they are two phases of the same underlying substance, physicists had not realized previously that the kinds of black holes we were studying and elementary particles are actually two phases of the same underlying stringy material. Whereas the surrounding temperature determines the phase in which water will exist, the topological form—the shape—of the extra Calabi-Yau dimensions determines whether certain physical configurations within string theory appear as black holes or elementary particles. That is, in the first phase, the initial Calabi-Yau shape (the analog of the ice phase, say), we find that there are certain black holes present. In the second phase, the second Calabi-Yau shape (the analog of the liquid water phase), these black holes have gone through a phase transition—they have "melted" so to speak—into fundamental vibrational string patterns. The tearing of space through conifold transitions takes us from one Calabi-Yau phase to the other. In so doing, we see that black holes and elementary particles, like water and ice, are two sides of the same coin. We see that black holes snugly fit within the framework of string theory.
We have purposely used the same water analogy for these drastic space-tearing transmutations and for the transmutations from one of the five formulations of string theory to another (Chapter 12) because they are deeply connected. Recall that we expressed through Figure 12.11 that the five string theories are dual to one another and thereby are unified under the rubric of a single overarching theory. But does the ability to move continuously from one description to another—to set sail from any point on the map of Figure 12.11 and reach any other—persist even after we allow the extra dimensions to curl up into some Calabi-Yau shape or another? Prior to the discovery of the drastic topology-changing results, the anticipated answer was no, since there was no known way to continuously deform one Calabi-Yau shape into any other. But now we see that the answer is yes: Through these physically sensible space-tearing conifold transitions, we can continuously change any given Calabi-Yau space into any other. By varying coupling constants and curled-up Calabi-Yau geometry, we see that all string constructions are, once again, different phases of a single theory. Even after curling up all extra dimensions, the unity of Figure 12.11 firmly holds.
Black Hole Entropy
For many years, some of the most accomplished theoretical physicists speculated about the possibility of space-tearing processes and of a connection between black holes and elementary particles. Although such speculations might have sounded like science fiction at first, the discovery of string theory, with its ability to merge general relativity and quantum mechanics, has allowed us now to plant these possibilities firmly at the forefront of cutting-edge science. This success emboldens us to ask whether any of the other mysterious properties of our universe that have stubbornly resisted resolution for decades might also succumb to the powers of string theory. Foremost among these is the notion of black hole entropy. This is the arena in which string theory has most impressively flexed its muscles, successfully solving a quarter-century-old problem of profound significance.
Entropy is a measure of disorder or randomness. For instance, if your desk is cluttered high with layer upon layer of open books, half-read articles, old newspapers, and junk mail, it is in a state of high disorder, or high entropy. On the other hand, if it is fully organized with articles in alphabetized folders, newspapers neatly stacked in chronological order, books arranged in alphabetical order by author, and pens placed in their designated holders, your desk is in state of high order or, equivalently, low entropy. This example illustrates the essential idea, but physicists have given a fully quantitative definition to entropy that allows one to describe something's entropy by using a definite numerical value: Larger numbers mean greater entropy, smaller numbers mean less entropy. Although the details are a little complicated, this number, roughly speaking, counts the possible rearrangements of the ingredients in a given physical system that leave its overall appearance intact. When your desk is neat and clean, almost any rearrangement—changing the order of the newspapers, books, or articles, moving the pens from their holders—will disturb its highly ordered organization. This accounts for its having low entropy. On the contrary, when your desk is a mess, numerous rearrangements of the newspapers, articles, and junk mail will leave it a mess and therefore will not disturb its overall appearance. This accounts for its having high entropy.
Of course, a description of rearranging books, articles, and newspapers on a desktop—and deciding which rearrangements "leave its overall appearance intact"—lacks scientific precision. The rigorous definition of entropy actually involves counting or calculating the number of possible rearrangements of the microscopic quantum-mechanical properties of the elementary constituents of a physical system that do not affect its gross macroscopic properties (such as its energy or pressure). The details are not essential so long as you realize that entropy is a fully quantitative quantum-mechanical concept that precisely measures the overall disorder of a physical system.
In 1970, Jacob Bekenstein, then a graduate student of John Wheeler's at Princeton, made an audacious suggestion. He put forward the remarkable idea that black holes might have entropy—and a huge amount of it. Bekenstein was motivated by the venerable and well-tested second law of thermodynamics, which declares that the entropy of a system always increases: Everything tends toward greater disorder. Even if you clean your cluttered desk, decreasing its entropy, the total entropy, including that of your body and the air in the room, actually increases. You see, to clean your desk you have to expend energy; you have to disrupt some of the orderly molecules of fat in your body to create this energy for your muscles, and as you clean, your body gives off heat, which jostles the surrounding air molecules into a higher state of agitation and disorder. When all of these effects are accounted for, they more than compensate for your desk's decrease in entropy, and thus the total entropy increases.
But what happens, Bekenstein in effect asked, if you clean your desk near the event horizon of a black hole and you set up a vacuum pump to suck all of the newly agitated air molecules from the room into the hidden depths of the black hole's interior? We can be even more extreme: What if the vacuum pumps all the air, and all the contents on the desk, and even the desk itself into the black hole, leaving you in a cold, airless, thoroughly ordered room? Since the entropy in your room has certainly decreased, Bekenstein reasoned that the only way to satisfy the second law of thermodynamics would be for the black hole to have entropy, and for this entropy to sufficiently increase as matter is pumped into it to offset the observed entropic decrease outside the black hole's exterior.
In fact, Bekenstein was able to draw on a famous result of Stephen Hawking's to strengthen his case. Hawking had shown that the area of the event horizon of a black hole—recall, this is the surface of no return that enshrouds every black hole—always increases in any physical interaction. Hawking demonstrated that if an asteroid falls into a black hole, or if some of the surface gas of a nearby star accretes onto the black hole, or if two black holes collide and combine—in any of these processes and all others as well, the total area of the event horizon of a black hole always increases. To Bekenstein, the inexorable evolution to greater total area suggested a link with the inexorable evolution to greater total entropy embodied in the second law of thermodynamics. He proposed that the area of the event horizon of a black hole provides a precise measure of its entropy.
On closer inspection, though, there are two reasons why most physicists thought that Bekenstein's idea could not be right. First, black holes would seem to be among the most ordered and organized objects in the whole universe. Once one measures the black hole's mass, the force charges it carries, and its spin, its identity has been nailed down precisely. With so few defining features, a black hole appears to lack sufficient structure to allow for disorder. Just as there is little havoc one can wreak on a desktop that holds solely a book and a pencil, black holes seem too simple to support disorder. The second reason that Bekenstein's proposal was hard to swallow is that entropy, as we have discussed it here, is a quantum-mechanical concept, whereas black holes, until recently, were firmly entrenched in the antagonistic camp of classical general relativity. In the early 1970s, without a way to merge general relativity and quantum mechanics, it seemed awkward, at best, to discuss the possible entropy of a black hole.
How Black Is Black?
As it turns out, Hawking too had thought of the analogy between his black hole area-increase law and the law of inevitable increase of entropy, but he dismissed it as nothing more than a coincidence. After all, Hawking argued, based upon his area-increase law and other results he had found with James Bardeen and Brandon Carter, if one did take the analogy between the laws of black holes and the laws of thermodynamics seriously, not only would one be forced to identify the area of the black hole's event horizon with entropy, but it turns out that one would also have to assign a temperature to the black hole (with the precise value determined by the strength of the black hole's gravitational field at its event horizon). But if a black hole has a nonzero temperature—no matter how small—the most basic and well-established physical principles would require it to emit radiation, much like a glowing poker. But black holes, as everyone knows, are black; they supposedly do not emit anything. Hawking and most everyone else agreed that this definitively ruled out Bekenstein's suggestion. Instead, Hawking was willing to accept that if matter carrying entropy is dropped into a black hole, this entropy is lost, plain and simple. So much for the second law of thermodynamics.
This was the case until Hawking, in 1974, discovered something truly amazing. Black holes, Hawking announced, are not completely black. If one ignores quantum mechanics and invokes only the laws of classical general relativity, then as originally found some six decades previously, black holes certainly do not allow anything—not even light—to escape their gravitational grip. But the inclusion of quantum mechanics modifies this conclusion in a profound way. Even though he was not in possession of a quantum-mechanical version of general relativity, Hawking was able to finesse a partial union of these two theoretical tools that yielded some limited yet reliable results. And the most important result he found was that black holes do emit radiation, quantum mechanically.
The calculations are long and arduous, but Hawking's basic idea is simple. We have seen that the uncertainty principle ensures that even the vacuum of empty space is a teeming, roiling frenzy of virtual particles momentarily erupting into existence and subsequently annihilating one another. This jittery quantum behavior also occurs in the region of space just outside the event horizon of a black hole. Hawking realized, however, that the gravitational might of the black hole can inject energy into a pair of virtual photons, say, that tears them just far enough apart so that one gets sucked into the hole. With its partner having disappeared into the abyss of the hole, the other photon of the pair no longer has a partner with which to annihilate. Instead, Hawking showed that the remaining photon gets an energy boost from the gravitational force of the black hole and, as its partner falls inward, it gets shot outward, away from the black hole. Hawking realized that to someone looking at the black hole from the safety of afar, the combined effect of this tearing apart of virtual photon pairs, happening over and over again all around the horizon of the black hole, will appear as a steady stream of outgoing radiation. Black holes glow.
Moreover, Hawking was able to calculate the temperature that a far-off observer would associate with the emitted radiation and found that it is given by the strength of the gravitational field at the black hole's horizon, exactly as the analogy between the laws of black hole physics and the laws of thermodynamics suggested.3 Bekenstein was right: Hawking's results showed that the analogy should be taken seriously. In fact, these results showed that it is much more than an analogy—it is an identity. A black hole has entropy. A black hole has temperature. And the gravitational laws of black hole physics are nothing but a rewriting of the laws of thermodynamics in an extremely exotic gravitational context. This was Hawking's 1974 bombshell.
To give you a sense of the scales involved, it turns out that when one carefully accounts for all of the details, a black hole whose mass is about three times that of the sun has a temperature of about a hundred-millionth of a degree above absolute zero. It's not zero, but only just. Black holes are not black, but only barely. Unfortunately, this makes a black hole's emitted radiation meager, and impossible to detect experimentally. There is, however, an exception. Hawking's calculations also showed that the less massive a black hole is, the higher its temperature and the greater the radiation it emits. For instance, a black hole as light as a small asteroid would emit about as much radiation as a million-megaton hydrogen bomb, with radiation concentrated in the gamma-ray part of the electromagnetic spectrum. Astronomers have searched the night sky for such radiation, but except for a few long-shot possibilities they have come up empty-handed, a likely indication that such low-mass black holes, if they exist, are very rare.4 As Hawking often jokingly points out, this is too bad, for if the black hole radiation that his work predicts were to be detected, he would undoubtedly win a Nobel Prize.5
By contrast with its tiny, sub-millionth of a degree temperature, when one calculates the entropy of, say, a three-solar-mass black hole, the result is an absolutely enormous number: a one followed by about 78 zeros! And the more massive the hole, the greater the entropy. The success of Hawking's calculations unequivocally established that this truly reflects the enormous amount of disorder embodied by a black hole.
But disorder of what? As we have seen, black holes appear to be terribly simple objects, so what is the source of this overwhelming disorder? On this question, Hawking's calculations were completely silent. His partial merger of general relativity and quantum mechanics could be used to find the numerical value of a black hole's entropy, but offered no insight into its microscopic meaning. For nearly a quarter of a century, some of the greatest physicists tried to understand what possible microscopic properties of black holes could account for their entropy. But without a fully trustworthy amalgam of quantum mechanics and general relativity, glimpses of an answer may have been uncovered, but the mystery remained unsolved.
Enter String Theory
Or, it did until January 1996, when Strominger and Vafa—building on earlier insights of Susskind and Sen—released a paper to the electronic physics archive entitled "Microscopic Origin of the Beckenstein-Hawking Entropy." In this work, Strominger and Vafa were able to use string theory to identify the microscopic constituents of a certain class of black holes and to calculate precisely their associated entropy. Their work relied on the newfound ability to partially circumvent the perturbative approximations in use during the 1980s and early 1990s, and the result they found agreed exactly with that predicted by Bekenstein and Hawking, finally completing a picture partially painted more than two decades previously.
Strominger and Vafa focused on the class of so-called extremal black holes. These are black holes that are imbued with charge—you can think of it as electric charge—and that, moreover, have the minimal possible mass consistent with the charge they carry. As can be seen from this definition, they are closely related to the BPS states discussed in Chapter 12. In fact, Strominger and Vafa exploited this similarity to the hilt. They showed that they could build—theoretically, of course—certain extremal black holes by starting with a particular collection of BPS branes (of certain specified dimensions) and binding them together according to a precise mathematical blueprint. In much the same way that an atom can be built—theoretically, again—by starting with a bunch of quarks and electrons and then precisely arranging them into protons and neutrons, surrounded by orbiting electrons, Strominger and Vafa showed how some of the newfound ingredients in string theory could similarly be molded together to yield particular black holes.
In actuality, black holes are one possible end product of stellar evolution. After a star has burned all its nuclear fuel through billions of years of atomic fusion, it no longer has the strength—the outward-directed pressure—to withstand the enormous inward force of gravity. Under a broad spectrum of conditions, this results in a cataclysmic implosion of the star's enormous mass; it violently collapses under its own tremendous weight, forming a black hole. Contrary to this realistic means of formation, Strominger and Vafa advocated "designer" black holes. They turned the tables on black hole formation by showing how they could be systematically constructed—in a theorist's imagination—by carefully, slowly, and meticulously weaving together a precise combination of the branes that had emerged from the second superstring revolution.
The power of this approach became immediately clear. By maintaining full theoretical control over the microscopic construction of their black holes, Strominger and Vafa could easily and directly count the number of rearrangements of the black hole's microscopic constituents that would leave its overall observable properties, its mass and force charges, unchanged. They could then compare this number with the area of the black hole's horizon—the entropy predicted by Bekenstein and Hawking. When Strominger and Vafa did so, they found perfect agreement. At least for the class of extremal black holes, they had succeeded in using string theory to account for the microscopic constituents and the associated entropy precisely. A quarter-century-old puzzle had been solved.6
Many string theorists view this success as an important and convincing piece of evidence in support of the theory. Our understanding of string theory is still too coarse to be able to make direct and precise contact with experimental observations of, say, the mass of a quark or an electron. But we now see that string theory has provided the first fundamental explanation of a long-established property of black holes that has stumped physicists using more conventional theories for many years. And this property of black holes is intimately tied up with Hawking's prediction that they should radiate, a prediction that, in principle, should be experimentally measurable. Of course, this requires that we definitively find a black hole in the heavens and then construct equipment sensitive enough to detect the radiation that it emits. If the black hole were light enough, the latter step is well within the reach of current technology. Even though this experimental program has not as yet met with success, it does re-emphasize that the chasm between string theory and definitive physical statements about the natural world can be bridged. Even Sheldon Glashow—the archrival of string theory through the 1980s—has said recently, "when string theorists talk about black holes they are almost talking about observable phenomena—and that is impressive."7
The Remaining Mysteries of Black Holes
Even with these impressive developments, there are still two central mysteries surrounding black holes. The first concerns the impact black holes have on the concept of determinism. In the beginning of the nineteenth century the French mathematician Pierre-Simon de Laplace enunciated the strictest and most far-reaching consequence of the clockwork universe that followed from Newton's laws of motion:
An intelligence that, at a given instant, could comprehend all the forces by which nature is animated and the respective situation of the beings that make it up, if moreover it were vast enough to submit these data to analysis, would encompass in the same formula the movements of the greatest bodies of the universe and those of the lightest atoms. For such an intelligence nothing would be uncertain, and the future, like the past, would be open to its eyes.8
In other words, if at some instant you know the positions and velocities of every particle in the universe, you can use Newton's laws of motion to determine—at least in principle—their positions and velocities at any other prior or future time. From this perspective, any and all occurrences, from the formation of the sun to the crucifixion of Christ, to the motion of your eyes across this word, strictly follow from the precise positions and velocities of the particulate ingredients of the universe a moment after the big bang. This rigid lock-step view of the unfolding of the universe raises all sorts of perplexing philosophical dilemmas surrounding the question of free will, but its import was substantially diminished by the discovery of quantum mechanics. We have seen that Heisenberg's uncertainty principle undercuts Laplacian determinism because we fundamentally cannot know the precise positions and velocities of the constituents of the universe. Instead, these classical properties are replaced by quantum wave functions, which tell us only the probability that any given particle is here or there, or that it has this or that velocity.
The downfall of Laplace's vision, however, does not leave the concept of determinism in total ruins. Wave functions—the probability waves of quantum mechanics—evolve in time according to precise mathematical rules, such as the Schrödinger equation (or its more precise relativistic counterparts, such as the Dirac equation and the Klein-Gordon equation). This informs us that quantum determinism replaces Laplace's classical determinism: Knowledge of the wave functions of all of the fundamental ingredients of the universe at some moment in time allows a "vast enough" intelligence to determine the wave functions at any prior or future time. Quantum determinism tells us that the probability that any particular event will occur at some chosen time in the future is fully determined by knowledge of the wave functions at any prior time. The probabilistic aspect of quantum mechanics significantly softens Laplacian determinism by shifting inevitability from outcomes to outcome-likelihoods, but the latter are fully determined within the conventional framework of quantum theory.
In 1976, Hawking declared that even this softer form of determinism is violated by the presence of black holes. Once again, the calculations behind this declaration are formidable, but the essential idea is fairly straightforward. When anything falls into a black hole, its wave function gets sucked in as well. But this means that in the quest to work out wave functions at all future times, our "vast enough" intelligence will be irreparably shortchanged. To predict the future fully we need to know all wave functions fully today. But, if some have escaped down the abyss of black holes, the information they contain is lost.
At first sight, this complication arising from black holes may not seem worth worrying about. Since everything behind the event horizon of a black hole is cut off from the rest of the universe, can't we just completely ignore anything that is unfortunate enough to have fallen in? Philosophically, moreover, can't we tell ourselves that the universe has not really lost the information carried by the stuff that has fallen into the black hole; it is simply locked within a region of space that we rational beings choose to avoid at all costs? Prior to Hawking's realization that black holes are not completely black, the answer to these questions was yes. But once Hawking informed the world that black holes radiate, the story changed. Radiation carries energy and so, as a black hole radiates, its mass slowly decreases—it slowly evaporates. As it does so, the distance from the center of the hole to the event horizon slowly shrinks, and as this shroud recedes, regions of space that were previously cut off re-enter the cosmic arena. Now our philosophical musings must face the music: Does the information contained in the things swallowed by the black hole—the data we imagined existing within the black hole's interior—re-emerge as the black hole evaporates? This is the information required for quantum determinism to hold, and so this question goes to the heart of whether black holes imbue the evolution of our universe with an even deeper element of happenstance.
As of this writing, there is no consensus among physicists regarding the answer to this question. For many years, Hawking has strongly claimed that the information does not re-emerge—that black holes destroy information thereby "introducing a new level of uncertainty into physics, over and above the usual uncertainty associated with quantum theory."9 In fact, Hawking, together with Kip Thorne of the California Institute of Technology, has a bet with John Preskill, also of the California Institute of Technology, regarding what happens to the information captured by a black hole: Hawking and Thorne bet that the information is forever lost, while Preskill has taken the opposite position and bet that the information re-emerges as the black hole radiates and shrinks. The wager? Information itself: "The loser(s) will reward the winner(s) with an encyclopedia of the winner's choice."
The bet remains unsettled, but Hawking has recently acknowledged that the newfound understanding of black holes from string theory, as discussed above, shows that there might be a way for the information to re-emerge.10 The new idea is that for the kind of black holes studied by Strominger and Vafa, and by many other physicists since their initial paper, information can be stored and recovered from the constituent branes. This insight, Strominger recently said, "has led some string theorists to want to claim victory—to claim that the information is recovered as black holes evaporate. In my opinion this conclusion is premature; there is still much work to be done in order to see if this is true."11 Vafa concurs, saying that he "is agnostic on this question—it could still turn out either way."12 Answering this question is a central goal of current research. As Hawking has put it,
Most physicists want to believe that information is not lost, as this would make the world safe and predictable. But I believe that if one takes Einstein's general relativity seriously, one must allow for the possibility that spacetime ties itself in knots and that information gets lost in the folds. Determining whether or not information actually does get lost is one of the major questions in theoretical physics today.13
The second unresolved black hole mystery concerns the nature of spacetime at the central point of the hole.14 A straightforward application of general relativity, going all the way back to Schwarzschild in 1916, shows that the enormous mass and energy crushed together at the black hole's center causes the fabric of spacetime to suffer a devastating rift, to be radically warped into a state of infinite curvature—to be punctured by a spacetime singularity. One conclusion that physicists drew from this is that since all of the matter that has crossed the event horizon is inexorably drawn to the center of the black hole, and since once there the matter has no future, time itself comes to an end at the heart of a black hole. Other physicists, who over the years have explored the properties of the black hole's core using Einstein's equations, revealed the wild possibility that it might be a gateway to another universe that tenuously attaches to ours only at a black hole's center. Roughly speaking, where time in our universe comes to an end, time in the attached universe just begins.
We will take up some of the implications of this mind-boggling possibility in the next chapter, but for now we want to stress one important point. We must recall the central lesson: Extremes of huge mass and small size leading to unimaginably large density invalidate the sole use of Einstein's classical theory and require that quantum mechanics be brought to bear as well. This leads us to ask, What does string theory have to say about the spacetime singularity at the center of a black hole? This is a topic of intense current research, but as with the question of information loss, it has not yet been settled. String theory deftly deals with a variety of other singularities—the rips and tears in space discussed in Chapter 11 and in the first part of this chapter.15 But if you have seen one singularity you have not seen them all. The fabric of our universe can be ripped, punctured, and torn in many different ways. String theory has given us profound insights into some of these singularities, but others, the black hole singularity among them, have so far eluded the string theorists' reach. The essential reason for this, once again, is the reliance on perturbative tools in string theory whose approximations, in this case, cloud our ability to analyze reliably and fully what happens at the deep interior point of a black hole.
However, given the recent tremendous progress in nonperturbative methods and their successful application to other aspects of black holes, string theorists have high hopes that it won't be long before the mysteries residing at the center of black holes start to unravel.