Complexity: A Guided Tour - Melanie Mitchell (2009)

Part II. Life and Evolution in Computers

Nature proceeds little by little from things lifeless to animal life in such a way that it is impossible to determine the exact line of demarcation.

—Aristotle, History of Animals

[W]e all know intuitively what life is: it is edible, lovable, or lethal.

—James Lovelock, The Ages of Gaia

Chapter 8. Self-Reproducing Computer Programs

What Is Life?

CHAPTER 5 DESCRIBED SOME OF THE HISTORY of ideas about how life has evolved. But a couple of things were missing, such as, how did life originate in the first place? And what exactly constitutes being alive? As you can imagine, both questions are highly contentious in the scientific world, and no one yet has definitive answers. Although I do not address the first question here, there has been some fascinating research on it in the complex systems community.

The second question—what is life, exactly?—has been on the minds of people probably for as long as “people” have existed. There is still no good agreement among either scientists or the general public on the definition of life. Questions such as “When does life begin?” or “What form could life take on other planets?” are still the subject of lively, and sometimes vitriolic, debate.

The idea of creating artificial life is also very old, going back at least two millennia to legends of the Golem and of Ovid’s Pygmalion, continuing in the nineteenth-century story of Frankenstein’s monster, all the way to the present era of movies such as Blade Runner and The Matrix, and computer games such as “Sim Life.”

These works of fiction both presage and celebrate a new, technological version of the “What is life?” question: Is it possible for computers or robots to be considered “alive”? This question links the previously separate topics of computation and of life and evolution.

You can ask ten biologists what are the ten key requisites for life and you’ll get a different list each time. Most are likely to include autonomy, metabolism, self-reproduction, survival instinct, and evolution and adaptation. As a start, can we understand these processes mechanistically and capture them in computers?

Many people have argued a vehement “no” for the following reasons:

Autonomy: A computer can’t do anything on its own; it can do only what humans program it to do.

Metabolism: Computers can’t create or gather their own energy from their environment like living organisms do; they have to be fed energy (e.g., electricity) by humans.

Self-reproduction: A computer can’t reproduce itself; to do so it would have to contain a description of itself, and that description would have to contain a description of itself, and so on ad infinitum.

Survival instinct: Computers don’t care whether they survive or not and they don’t care how successful they are. (For example, in a lecture I attended by a prominent psychologist, the speaker, discussing the success of computer chess programs, asserted that “Deep Blue may have beat Kasparov, but it didn’t get any joy out of it.”)

Evolution and adaptation: A computer can’t evolve or adapt on its own; it is restricted to change only in ways specified ahead of time by its programmer.

Although these arguments are still believed by many people, all of them have been claimed to be disproven in one way or another in the field of artificial life, whose purview is the simulation and “creation” of life on computers. In this chapter and the next I focus on those issues most closely related to Darwinism—self-reproduction and evolution.

Self-Reproduction in Computers

The self-reproduction argument is the most mathematical one: it states that self-reproduction in a computer would lead to an infinite regress.

Let’s investigate this issue via the simplest version of the computer self-reproduction problem: write a computer program that prints out an exact copy of itself and nothing else.

I’ve written the following programs in a simple computer language that even nonprogrammers should be able to understand. (It’s actually a pseudo language, with a few commands that most real languages wouldn’t have, but still plausible and thrown in to make things simpler.)

Here’s a first attempt. I start out with the name of the program:

program copy

Now I need to add an instruction to print out the name of the program:

program copy print("program copy")

The print command simply prints on the computer screen the characters between the first and last quotation marks, followed by a carriage return. Now I need to add an instruction to print out that second line:

program copy print("program copy") print(" print("program copy")")

Note that, since I want the program to print out an exact copy of itself, the second print command has to include the four spaces of indentation I put before the first print command, plus the two quotation marks, which are now themselves being quoted (the print command prints anything, including quotation marks, between the outermost quotation marks). Now I need another line to print out that third line:

program copy print("program copy") print(" print("program copy")") print(" print(" print("program copy")")")

and so forth. By now you can probably see how this strategy, in which each command prints an exact copy of the command preceding it, leads to an infinite regress. How can this be avoided? Before reading on, you might spend a few moments trying to solve this puzzle.

This simple-sounding problem turns out to have echos in the work of Kurt Gödel and Alan Turing, which I described in chapter 4. The solution also contains an essential means by which biological systems themselves get around the infinite regress. The solution was originally found, in the context of a more complicated problem, by the twentieth-century Hungarian mathematician John von Neumann.

Von Neumann was a pioneer in fields ranging from quantum mechanics to economics and a designer of one of the earliest electronic computers. His design consisted of a central processing unit that communicates with a random access memory in which both programs and data can be stored. It remains the basic design of all standard computers today. Von Neumann was also one of the first scientists who thought deeply about connections between computation and biology. He dedicated the last years of his life to solving the problem of how a machine might be able to reproduce itself; his solution was the first complete design for a self-reproducing machine. The self-copying computer program I will show you was inspired by his “self-reproducing automaton” and illustrates its fundamental principle in a simplified way.

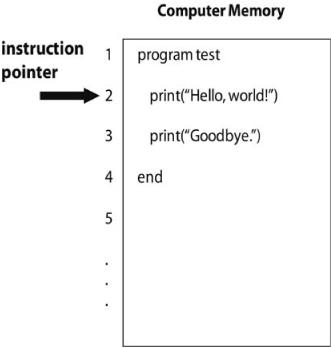
FIGURE 8.1. A simplified picture of computer memory, with numbered locations 1-5 and beyond, four of which contain lines of a program. The instruction pointer points to the instruction currently being executed by the computer. The lines sometimes contain leading spaces, which are ignored when the instruction is executed.

Before showing you the self-copying program, I need to explain a few more things about the programming language I will be using.

Consider the picture of computer memory given in figure 8.1. Computer memory, in our highly simplified case, consists of numbered locations or “addresses,” here numbered 1-5 and beyond. Each location contains some text. These lines of text can be interpreted by the computer as commands in a program or as data to be used by a program. The program currently stored in memory, when executed, will print

Hello, world! Goodbye.

To accomplish this, the computer has an “instruction pointer”—a number also stored in memory, which always is equal to the memory location of the instruction currently being executed by the computer. The instruction pointer—let’s call it ip for short—is initially set to the memory location containing the program’s first line. We say it “points to” that instruction. At each step in the computation the instruction pointed to by ip is carried out, and ip is increased by 1.

For example, in figure 8.1, the value of ip is 2, and we say that ip is pointing to the line print("Hello, world!").

We call ip a variable since its value changes (“varies”) as the computation is carried out.

We also can define another variable, line[n], as equal to the string of characters in memory location n. For example, the command print(line[2]) will print

print(”Hello, world!”)

Finally, our language contains a loop command. For example, the following lines of computer code,

x = 0 loop until x = 4 { print(”Hello, world!”) x = x + 1 }

will print

Hello, world! Hello, world! Hello, world! Hello, world!

The commands inside the two curly brackets get repeated until the loop condition (here x = 4) is true. The variable x is used as a counter—it starts off at zero and is increased by 1 each time the loop is performed. When it gets to 4, the loop stops.

Now we are ready for the self-copying program, which appears in its entirety in figure 8.2. The best way to understand a computer program is to hand-simulate it; that is, to go through it line by line keeping track of what it does.

Suppose this program has been loaded into computer memory as shown in figure 8.2, and suppose a user comes along and types selfcopy on the computer’s command line. This signals the computer to start interpreting the program called selfcopy. The interpreter—part of the computer’s operating system—sets the instruction pointer to 1, which points to the name of the program. The ip then moves down, line by line, executing each instruction.

FIGURE 8.2. A self-copying program.

In memory location 2 a variable L is set to ip−1. Recall that ip is the location of the instruction currently being executed. So when line 2 is executed, ip is set to 2 and L is set to 2 − 1 = 1. (Note that L will now stay equal to 1 until it is reset, even though ip changes as each instruction is executed.)

Next, a loop is entered, which will be iterated until line[L] is equal to the character string end. Remember that line[L] is equal to the string located in memory location L. Right now, L is set to 1, so line[L] is equal to the string program selfcopy. This is not equal to the string end, so the loop is continued. In the loop, line[L] is printed and L is incremented. First, with L = 1, program selfcopy is printed; then L is set to 2.

Now, line[L] is the second line of the program, namely L = ip - 1. Again, this string is not equal to end, so the loop is continued. In this way, each line of the program is printed out. A particularly interesting line is line 5: when line 5 is being executed with L = 5, the instruction print(line[L]) prints itself out. When L = 9 and line[L] is equal to end, the loop ends. At this point, lines 1-8 have been printed. The instruction pointer moves to line 8 (the instruction immediately following the loop), which, when executed, prints out the string “end,” completing the self-copying.

The essence of self-copying in this program is to use the same information stored in memory in two ways: first as instructions to be executed, and second as data to be used (i.e., printed) by those instructions. This dual use of information is what allows us to avoid an infinite regress of the kind illustrated earlier by my first attempt at a self-copying program.

The Deeper Meaning of the Self-Reproducing
Computer Program

The dual use of information is also at the heart of Gödel’s paradox, embodied by his self-referential sentence “This statement is not provable.”

This is a bit tricky to understand. First, let’s note that this sentence, like any other English sentence, can be looked at in two ways: (1) as the literal string of letters, spaces, and punctuation contained in the sentence, and (2) as the meaning of that literal string, as interpreted by an English speaker.

To be very clear, let’s call the literal string of characters S. That is, S = “This statement is not provable.” We can now state facts about S: for example, it contains twenty-six letters, four spaces, and one period.

Let’s call the meaning of the sentence M. We can rewrite M as follows: “Statement S is not provable.” In a way, you can think of M as a “command” and of S as the “data” for that command. The weird (and wonderful) thing is that the data S is the same thing as the command M. The chief reason Gödel was able to translate his English sentence into a paradox in mathematics was that he was able to phrase M as a mathematical statement and S as a number that encoded the string of characters of that mathematical statement.

This is all very tricky. This kind of distinction between literal strings of characters and the meaning of those strings, and the paradoxes that self-reference can produce, are discussed in a detailed and very entertaining way in Douglas Hofstadter’s book Gödel, Escher, Bach: an Eternal Golden Braid.

Similarly, this kind of dual use of information is key to Turing’s proof of the undecidability of the Halting problem. Remember H and H from chapter 4? Do you recall how H ran on its own code? That is, just like our self-reproducing computer program above, H was used in two ways: as an interpreted program and as the input for that program.

Self-Replication in DNA

At this point you may be groaning that we’re back in the abstract realm of logical headaches. But give me a minute to bring us back to reality. The really amazing thing is that this dual use of information is key to the way DNA replicates itself. As I described in chapter 6, DNA is made up of strings of nucleotides. Certain substrings (genes) encode amino acids making up proteins, including the enzymes (special kinds of proteins) that effect the splitting of the double helix and the copying of each strand via messenger RNA, transfer RNA, ribosomes, et cetera. In a very crude analogy, the DNA strings encoding the enzymes that perform the copying roughly correspond to the lines of code in the self-copying program. These “lines of code” in DNA are executed when the enzymes are created and act on the DNA itself, interpreting it as data to be split up and copied.

However, you may have noticed something I have so far swept under the rug. There is a major difference between my self-copying program and DNA self-reproduction. The self-copying program required an interpreter to execute it: an instruction pointer to move down the lines of computer code and a computer operating system to carry them out (e.g., actually perform the storing and retrieving of internal variables such as ip and L, actually print strings of characters, and so on). The interpreter is completely external to the program itself.

In contrast, in the case of DNA, the instructions for building the “interpreter”—the messenger RNA, transfer RNA, ribosomes, and all the other machinery of protein synthesis—are encoded along with everything else in the DNA. That is, DNA not only contains the code for its self-replicating “program” (i.e., the enzymes that perform the splitting and copying of DNA) but also it encodes its own interpreter (the cellular machinery that translates DNA into those very enzymes).

Von Neumann’s Self-Reproducing Automaton

Von Neumann’s original self-reproducing automaton (described mathematically but not actually built by von Neumann) similarly contained not only a self-copying program but also the machinery needed for its own interpretation. Thus it was truly a self-reproducing machine. This explains why von Neumann’s construction was considerably more complicated than my simple self-copying program. That it was formulated in the 1950s, before the details of biological self-reproduction were well understood, is testament to von Neumann’s insight. Von Neumann’s design of this automaton and mathematical proof of its correctness were mostly completed when he died in 1957, at the age of 53, of cancer possibly caused by his exposure to radiation during his work on the atomic bomb. The proof was completed by von Neumann’s colleague, Arthur Burks. The complete work was eventually published in 1966 as a book, Theory of Self-Reproducing Automata, edited by Burks.

John von Neumann, 1903-1957 (AIP Emilio Segre Visual Archives)

Von Neumann’s design for a self-reproducing automaton was one of the first real advances in the science of artificial life, demonstrating that self-reproduction by machine was indeed possible in principle, and providing a “logic” of self-reproduction that turned out to have some remarkable similarities to the one used by living systems.

Von Neumann recognized that these results could have profound consequences. He worried about public perception of the possibilities of self-reproducing machines, and said that he did not want any mention of the “reproductive potentialities of the machines of the future” made to the mass media. It took a while, but the mass media eventually caught up. In 1999, computer scientists Ray Kurzweil and Hans Moravec celebrated the possibility of super-intelligent self-reproducing robots, which they believe will be built in the near future, in their respective nonfiction (but rather far-fetched) books The Age of Spiritual Machines and Robot. In 2000 some of the possible perils of self-reproducing nano-machines were decried by Bill Joy, one of the founders of Sun Microsystems, in a now famous article in Wired magazine called “Why the Future Doesn’t Need Us.” So far none of these predictions has come to pass. However, complex self-reproducing machines may soon be a reality: some simple self-reproducing robots have already been constructed by roboticist Hod Lipson and his colleagues at Cornell University.

John von Neumann

It is worth saying a few words about von Neumann himself, one of the most important and interesting figures in science and mathematics in the twentieth century. He is someone you should know about if you don’t already. Von Neumann was, by anyone’s measure, a true genius. During his relatively short life he made fundamental contributions to at least six fields: mathematics, physics, computer science, economics, biology, and neuroscience. He is the type of genius whom people tell stories about, shaking their heads and wondering whether someone that smart could really be a member of the human species. I like these stories so much, I want to retell a few of them here.

Unlike Einstein and Darwin, whose genius took a while to develop, Hungarian born “Johnny” von Neumann was a child prodigy. He supposedly could divide eight-digit numbers in his head at the age of six. (It evidently took him a while to notice that not everyone could do this; as reported in one of his biographies, “When his mother once stared rather aimlessly in front of her, six-year-old Johnny asked: ‘What are you calculating?’ ”) At the same age he also could converse with his father in ancient Greek.

At the age of eighteen von Neumann went to university, first in Budapest, then in Germany and Switzerland. He first took the “practical” course of studying chemical engineering but couldn’t be kept away from mathematics. He received a doctorate in math at the age of twenty-three, after doing fundamental work in both mathematical logic and quantum mechanics. His work was so good that just five years later he was given the best academic job in the world—a professorship (with Einstein and Gödel) at the newly formed Institute for Advanced Study (IAS) in Princeton.

The institute didn’t go wrong in their bet on von Neumann. During the next ten years, von Neumann went on to invent the field of game theory (producing what has been called “the greatest paper on mathematical economics ever written”), design the conceptual framework of one of the first programmable computers (the EDVAC, for which he wrote what has been called “the most important document ever written about computing and computers”), and make central contributions to the development of the first atomic and hydrogen bombs. This was all before his work on self-reproducing automata and his exploration of the relationships between the logic of computers and the workings of the brain. Von Neumann also was active in politics (his positions were very conservative, driven by strong anti-communist views) and eventually became a member of the Atomic Energy Commission, which advised the U.S. president on nuclear weapons policy.

Von Neumann was part of what has been called the “Hungarian phenomenon,” a group of several Hungarians of similar age who went on to become world-famous scientists. This group also included Leo Szilard, whom we heard about in chapter 3, the physicists Eugene Wigner, Edward Teller, and Denis Gabor, and the mathematicians Paul Erdös, John Kemeny, and Peter Lax. Many people have speculated on the causes of this improbable cluster of incredible talent. But as related by von Neumann biographer Norman MacRae, “Five of Hungary’s six Nobel Prize winners were Jews born between 1875 and 1905, and one was asked why Hungary in his generation had brought forth so many geniuses. Nobel laureate Wigner replied that he did not understand the question. Hungary in that time had produced only one genius, Johnny von Neumann.”

Von Neumann was in many ways ahead of his time. His goal was, like Turing’s, to develop a general theory of information processing that would encompass both biology and technology. His work on self-reproducing automata was part of this program. Von Neumann also was closely linked to the so-called cybernetics community—an interdisciplinary group of scientists and engineers seeking commonalities among complex, adaptive systems in both natural and artificial realms. What we now call “complex systems” can trace its ancestry to cybernetics and the related field of systems science. I explore these connections further in the final chapter.

Von Neumann’s interest in computation was not always well received at the elite Institute for Advanced Study. After completing his work on the EDVAC, von Neumann brought several computing experts to the IAS to work with him on designing and building an improved successor to EDVAC. This system was called the “IAS computer”; its design was a basis for the early computers built by IBM. Some of the “pure” scientists and mathematicians at IAS were uncomfortable with so practical a project taking place in their ivory tower, and perhaps even more uncomfortable with von Neumann’s first application of this computer, namely weather prediction, for which he brought a team of meteorologists to the IAS. Some of the purists didn’t think this kind of activity fit in with the institute’s theoretical charter. As IAS physicist Freeman Dyson put it, “The [IAS] School of Mathematics has a permanent establishment which is divided into three groups, one consisting of pure mathematics, one consisting of theoretical physicists, and one consisting of Professor von Neumann.” After von Neumann’s death, the IAS computer project was shut down, and the IAS faculty passed a motion “to have no experimental science, no laboratories of any kind at the Institute.” Freeman Dyson described this as, “The snobs took revenge.”