The Philosophy of Physics (2016)

1
Interpreting Physical Theories

In this chapter we get to grips with what philosophy of physics is all about and what kinds of questions it deals with. We also introduce some basic general concepts and terminology from philosophy: ontology, epistemology, etc. And also introduce such essential philosophy of science concepts as ‘theory,’ ‘model’ and so on - the concepts on which our later discussions will be based (the tools of the trade, so to speak). A key point that will be emphasized here is that there is often a difficulty in understanding how some (empirically) successful theory (formulated in ‘the language of mathematics’) can map on to physical reality - there is an additional question discussed of how mathematics can perform its feat of allowing the formulation of precise, successful physical laws. There is often, for example, a multiplicity of possible ‘ways the world could be’ according to the mathematical structure, while still preserving the theory’s empirical success. We indicate that symmetries often lie at the root of (the most interesting of) these situations - a fact that will form the basis of much of this book.

1.1 Does the World Need Philosophers of Physics?

Does the world really have any need for philosophers of physics and the odd trade they ply? If we were to put them all on a spacecraft, in the style of the Hitchhiker’s Guide to the Galaxy, say, on the Golgafrincham Ark Fleet’s ‘Ship B,’ occupied by telephone sanitizers, public relations executives, advertising account executives, and other such ‘worthy’ tradespeople, would the human race be worse off or all the better for it?

Of course “need” can mean many things, each depending on the purpose or use. If we believe that there is a need to think especially deeply about physical theories, about why they work so well, and what they can tell us about the nature of reality: then there is a need for philosophers of physics. If we mean is there a practical use for philosophy of physics, then it is less clear that they have anything to contribute to the world, though that is not a clear-cut matter. But the main problem we face in answering this question is knowing where to draw the line between physics and philosophy of physics. If we were to end up throwing David Bohm, Niels Bohr, Albert Einstein, Werner Heisenberg, Erwin Schrödinger, and Hermann Weyl onto Ship B then you would agree, I hope, that the world would be all the worse for it. Yet each of these physicists was a ‘philosopher-physicist’: they even wrote books on the philosophy of physics. In days gone past they would have been called ‘natural philosophers,’ like Newton. I think natural philosophy is still a very useful term to use to describe one who studies the natural sciences philosophically, and if I had my way it would be back in operation to describe philosophers of physics and philosopher-physicists. I can think of several living (as of 2015, and long may they continue) physicists that fit the traditional mold of natural philosopher, among them Julian Barbour, Rudolph Haag, Roger Penrose, Carlo Rovelli, Lee Smolin, Max Tegmark, Gerard’t Hooft, and Dieter Zeh. What characterizes them is that they think deeply about the foundations of their subject, and especially about the nature of space, time, and matter: our primary subject matter (or rather, the subject matter of our subject matter: theories of space, time, and matter).

And yet the philosophy of physics is often frowned upon by physicists. When physicists lapse into discussing philosophy it is seen to be just that: a lapse. Richard Feynman is famously reported to have said that “Philosophy of science is about as useful to scientists as ornithology is to birds” - there is a fairly sizeable catalogue of Feynman’s anti-philosophy quotes to draw from and I think much of today’s anti-philosophical spirit has a lot to do with Feynman worship (though there are many worse people to worship…). Again, as above, this might well be true, of course, depending on how one interprets ‘useful.’ ‘Use’ is just like ‘need’ again. When it comes to computing values of physical quantities to be compared with experiment, admittedly philosophers might not be of much use. They won’t be too upset that they aren’t of use in this sense: it’s not what they live for. But if one is facing some problem in the foundations of physics, then the more generalist approach of a philosopher (or a philosophical approach) might be of some use after all - likewise, ornithology might well be useful to birds, in terms of conservation of a species for example!

Need and usefulness need to be more carefully circumscribed. One can easily make a case for a need for a philosophical approach to physics, and for the usefulness of such an approach. Given this, one can make a case for having a specific discipline, a dedicated community of scholars, devoted to such an approach, putting aside as secondary those core aspects of physics itself. Hence, becoming a philosopher of physics rather than a physicist involves a trade-off: you put the computing-intensive aspects aside in favor of the critical, interpretive aspects. Some people can do both, but they are the exception.

A philosophical approach to physics will direct attention to aspects of physics that are usually deemed sacred by the average practicing physicist. This can lead to advances by opening up new lines of enquiry, suggesting hypotheses that would be unthinkable at the everyday level of physics. In this book we will meet several examples in which this has occurred, mostly based on the work of philosopher-physicists. One often finds that thought experiments (or gedanken experiments) lie at the root of the really major advances in physics, the revolutions. Such thought experiments usually probe some foundational assumption, concerning space, time, locality, causality, determinism, matter, force, and so on. This kind of approach amounts to philosophical thinking (in the sense of conceptual analysis).

In this sense, then, philosophy is a fundamental part of the development of physics. One can’t really do physics without making certain assumptions, however minimal, about how the theories one is using map onto reality (even if it is only mapping onto observable reality, as some believe [anti-realists, such as instrumentalists or constructive empiricists, who give unobservables the ‘silent treatment’], though even this is not so benign a claim as they think).1 One needs to take a stance on what the components of the theories refer to, what they are about (this is the meaning of the philosophical term ‘ontology’: what there is).

This is one of the primary functions of philosophers of physics: interpretation of physical theories (on which, see §1.3 below). Mapping between theory and world. It is almost never a trivial matter; especially since physical theories often make use of all sorts of idealizations, approximations, and indirect methods of representing their ‘target’ systems. A key assumption underlying philosophy of physics, then, is that the job of physics is to say something about the structure of reality, about what the universe is really like: what objects there are, what properties they have, how they behave, how they relate to one another, and so on. Much of this book will be devoted to specific examples of this type and will highlight the ways in which interpretive controversies emerge. The interpretive controversies point to the existence of ‘epistemological’ considerations: what we can know. If there are multiple possible interpretations of some theory, then it seems we are limited in what a theory can tell us about the world. We will meet this in a very stark way in §5.1, in which an argument is presented that claims to show that our choice of world-geometry is largely conventional (that is, there is no fact of the matter that can decide, so we use other considerations to choose). We consider what interpretation amounts to in §1.3. First, let’s take a look at a historical feature of philosophy of physics: the issue of its relative recency.

1.2 Why No Ancient Philosophy of Physics?

Philosophy of physics is a fairly modern discipline, emerging from various specializations that occurred at the close of the nineteenth century. Why didn’t philosophy of physics exist earlier? Why wasn’t there such a thing in the days of Democritus and Parmenides? We are happy to still discuss Newtonian mechanics as philosophers of physics, but it seems that stretching further back doesn’t quite work in the same way (even with Plato and Aristotle): why is this? One important factor is that the pre-Socratics, and those working before the Medieval period, relied on naked eye observations. There were no amplifications of vision as there have been since Galileo modified the looking glass (until then a simple gypsy toy) into a telescope for scientific usage. There was, in fact, no real experimental method. Some kinds of experiments could no doubt be said to have occurred, but this was not viewed as the royal road to worldly knowledge as it is today. This meant that theoretical structures were far more heavily based on what was delivered through the senses. However, as we will see in a moment, this wasn’t always the case, and unobservables invoked to explain observables can be found in theories in the earliest fragments of writing.

Modern philosophy of physics would be unimaginable without theories that can be put into a fairly standard mathematical form. For example, spacetime theories are presented through ‘models’ of the form , consisting of some basic set of point-elements ℳ (a set of points with a certain size or cardinality) on which is imposed various levels of additional structure that let one talk about, e.g. the dimension of the space, the nearness of points, the distance of points, volumes, parallelism, and so on. This then provides the basic object whose mapping onto the world (or a world) we must, wearing our philosophy of physics hats, consider - that is, we must provide an interpretation. This will involve setting up a correspondence between mathematical entities, ⟨the set of mathematical points and mathematical relationships between such points⟩, and ⟨things and their properties in the world⟩.

This provides a second factor for the relative recency of philosophy of physics: earlier work was less mathematical, or entirely non-mathematical. The development of calculus in particular was pivotal in the development of a physics that was able to make precise predictions and allow thinking in terms of present (initial) conditions generating future states. Also, more conceptually, the notion of a ‘law of nature’ (understood as an expression of invariance or constancy) was fairly slow to emerge, and can be seen to receive its enunciation with Galileo - though, even here, it is expressed in the form of a dialogue rather than in formal terminology.2

In fact, inasmuch as there were theories proposed by Democritus and Parmenides, there is something that might very loosely be called ‘philosophy of ancient physics’ (i.e. rather than ancient philosophy of physics). Those theories tended to focus on cosmological issues and were largely a priori (that is, based on reason and logic rather than experience). What we have from these philosophers are mere fragments. In the case of Parmenides we only have a fragment of a poem (160 lines of a supposed 800-line work). However, we can find strikingly similar dichotomies to those found in modern theories: discrete versus continuous space; infinite versus finite space; real time versus illusory time; eternal time versus beginning of time; plenum versus void; many worlds versus one world; and so on. There are also discussions of motion and its relationship with space and time, along with the ramifications a denial of the former has on the latter, and vice versa. Let us mention some of these views, since they provide a nice route into some of the more modern debates we discuss later.

Though I downplayed the mathematical nature of early theories, Zeno can with some justification be said to have considered a mathematical account of space, time, and motion, if only to dismiss its applicability to the real world, on pain of generating paradoxes. Take, for example, the so-called ‘paradox of plurality.’ Here we are asked to consider an extended object: a 5 cm long line, say. We can envisage splitting this into two pieces, and then splitting those two pieces each into two more pieces, and so on. How will this process end if space is infinitely divisible? Zeno suggests two possibilities: (1) with points of some finite (though minuscule) size, or (2) with points of zero size. But neither is acceptable, says Zeno: if the points have some size, then given we have made infinite divisions, there will be infinitely many, which will certainly not generate a 5 cm line when aggregated. But if the points have zero size, then not even an infinity of them will aggregate to form a 5 cm line. Or consider ‘the arrow paradox.’ Here the punchline is that an arrow in flight can never be in motion at any instant, since it will be at rest at an instant; if it weren’t, the instant must have parts, and so not be indivisible. And yet it somehow gets from one instant to the next. In some ways this is a motion-based analogue of the plurality paradox: how can we add up lots of stationary pieces to get an extended motion? The stimulating effect on future physics (and mathematics) cannot be overestimated.3

If a mathematical account of space, time, and motion (in terms of continuous, infinitely divisible entities and processes) is to be carried out, then Zeno’s challenges would have to be met. If they could not be met, then at the very least there would be a gap between model and reality. Atomism was one early response to the challenge: if space (and perhaps time) could not be infinitely divided, then Zeno’s division paradoxes don’t hold water. In any case, they shift attention to the possible structure of space and time: what kind of things they are. And motion is implicated in this structural exploration.

We can also fit earlier theories, such as Aristotle or Plato’s cosmology, into the mold of the model-based approach mentioned above. In these cosmologies there is a preferred location in the universe corresponding to the Earth’s position in space, which is assumed to be at absolute rest (which makes intuitive sense, of course, since we don’t seem to be moving when we ourselves remain at rest relative to the Earth). The universe is, in this scheme, spherical, with the Earth at the dead center, stationary and not rotating, and the Moon, Mercury, Venus, the Sun, Mars, Jupiter, and Saturn occupying (in this order outwards from the Earth) concentric spheres - beyond this lies ‘the firmament,’ an outmost layer of fixed stars providing an ‘edge’ to the universe (an idea mocked by Archytas who asked what would happen if we poke a stick or a hand outwards from this layer - see fig. 1.1). This allows for talk of absolute distances (and absolute notions of ‘up’ and ‘down’) by using the Earth’s perspective as the origin. Of course, the Copernican revolution would dislodge this special perspective by dislodging the specialness of the location of the Earth and its relationship to the other planets and stars.

Fig. 1.1 A woodcut by Camille Flammarion showing Archytas’ thought experiment in action, breaking through Aristotle’s closed universe with his stick and his hand, to reveal more space.

[Source: C. Flammarion, L'Atmosphere: Météorologie Populaire (Paris, 1888: p. 163)].

In the Aristotelian universe there are five elements (Aether, Fire, Air, Water, and Earth) that have ‘natural places’ that determine their behaviors (natural motions) relative to the Earth’s frame. This is a teleological world in which things are guided by where they should be: fire wants to rise; earth wants to fall. This is a law of sorts, and it is based to some extent on observations. But it certainly doesn’t have same level of rigor of modern physical laws, nor does it strike one as particularly explanatory, nor does it seem capable of generating very interesting predictions. Rather, the fact that, e.g. the stars are found to move in a circular fashion, is made a necessary part of the world: this is what stars must do, and such things constrained to move in circles should be given a special name (this circular motion is the essential quality of aether from which the heavenly bodies are made). This circularity property was a key part of Plato’s Timaeus, in which his cosmology was laid out. Later, in his Almagest, Ptolemy converted this idea (of circular, uniform planetary motion) into a mathematical model (based on nothing but circular regular motions) capable of delivering predictions of our apparently rather messy, irregular world. ‘Model’ in this sense is meant in terms of an approximate representation, not an exact one-to-one correspondence with ‘the way things are.’ Philosophers since Plato have spoken of this kind of modeling as ‘saving the phenomena’: the recovery (by means of a theory or model) of the way the world appears to us.

But, more importantly, there is a detailed discussion of the notion of space in Aristotle and Plato. This was identified with ‘place’ in their schemes. Aristotle’s account is more detailed. His view is ‘plenistic,’ meaning that space (the universe) is viewed as always full (with no genuinely empty spaces): if some portion of space is not occupied by water or matter it is occupied by air, each displacing one or the other as they are moved. As mentioned above, this was combined with a theory of ‘natural place’ whereby each kind of thing is transported to its own specific category of place (hence, the teleological notion of a ‘final’ or ‘future cause’ in this case). The notion of a natural motion (in which a body finds its ‘proper place’) and a ‘forced (or “violent”) motion’ (in which a body is taken off its proper course by some intervention) is the origin of the modern concepts of kinematics and dynamics respectively, which we will meet again.

In his Timaeus, Plato also defends the view that the world is a plenum: matter and space are, in fact, identified. Aristotle, however, introduces place as a kind of entity independent from matter, since while matter (and the form the matter takes) are essential to a body, place is not: different objects can occupy the same space, and the same object can occupy different places. Place itself is defined in terms of objects, however. It is the two-dimensional boundary of the body it contains, which it is in contact with. It is presented by Aristotle (in his Physics, Book IV) using the analogy of a (motionless) container, in fact. This metaphor persists into the modern debate between so-called ‘substantivalists’ (who view space as a real container) and ‘relationists’ (who view space as nothing over and above the relations between things) - see §4.1. However, Aristotle doesn’t sit completely comfortably in either camp, though he is usually aligned with relationism since places are defined by the boundaries of objects: no objects, no boundaries, no places.

Time was, in Aristotle’s picture, similarly related to physical entities, in this case changes (of places or properties of things): no change = no time. The measure of time was linked, then, to (uniform) motion - though it is not identified with motion and change: how could it be? (1) motion is attached to the thing moving, while time stretches out everywhere, and (2) motions vary in speed, but time does not. Indeed, Aristotle speaks of time’s being a ‘measure of motion’ in the same way as the cubit measures lengths. In the case of time the unit (analogous to the cubit) is provided by the revolution of the outermost sphere of the heavens. But Aristotle can be found intellectually struggling with the status of time, as with space: are they ‘real’ or not (i.e. in the world or in the mind)? If they are real, how closely linked are they to their measures (cubits, revolutions, and the like)? For Aristotle, motion is ontologically (and logically) prior to time: the latter is defined in terms of the former. Such probing is at the heart of philosophy of physics, and the same questions (and often similar responses) arise again and again over the two millennia connecting Aristotle with us.

1.3 The Interpretation Game

If the primary task of the physicist is to construct models and theories of the world, the primary task of a philosopher of physics is to interpret these products of physics, be they theories, models, simulations, or experiments (including so-called ‘thought experiments’). That is, suppose that we believe one of these constructions: what must the world be like to ground the belief? We needn’t trouble ourselves with questions of truth and realism; though connected, that’s strictly a separate matter. We can think about ‘model worlds’ (possible worlds) that ground the belief instead. Our own, actual world might be among this class of possible worlds, but it is not necessary in order to provide an interpretation (and an associated ontological picture).

In this book we shall focus on theories, models, and thought experiments and the possible relationship they bear to physical reality. Understanding what a theory or model says about reality is to offer an interpretation. As mentioned above, it involves ‘mapping the theory to the world.’ Usually it is no simple matter, and many possibilities are available. Hence we often face a problem of interpretation (for some theory or model) in that there can be many interpretations compatible both with the same theory or model and with what we observe with the naked senses or experiment. Of course, this demands a thorough discussion of what we mean by ‘theory’ and ‘model’ (the targets of our interpretations) - we gave a very brief description above, but the issue forms an entire project in philosophy of science.4

One can understand this situation as somewhat similar to the interpretation of a Rorschach test in psychoanalysis (see fig. 1.2). Here a variety of inkblots are shown to a subject who is then asked to comment on what he sees. The inkblots look random, but are (supposedly) well-chosen and presented in a sequence of ten ever more complex (and [supposedly] more revealing) blots. The subject will interpret the print in such a way as, so the idea goes, to give some clues as to the nature of their personality, including any disorders or past traumas they may have suffered and buried in their subconscious. If someone sees a fluffy bunny in the image, then we are led to think that they will not be an axe murderer, though they may be a little soft in the head. However, if a scene of human sacrifice is seen in the same image by someone else, then it’s time to call in the men in white coats!

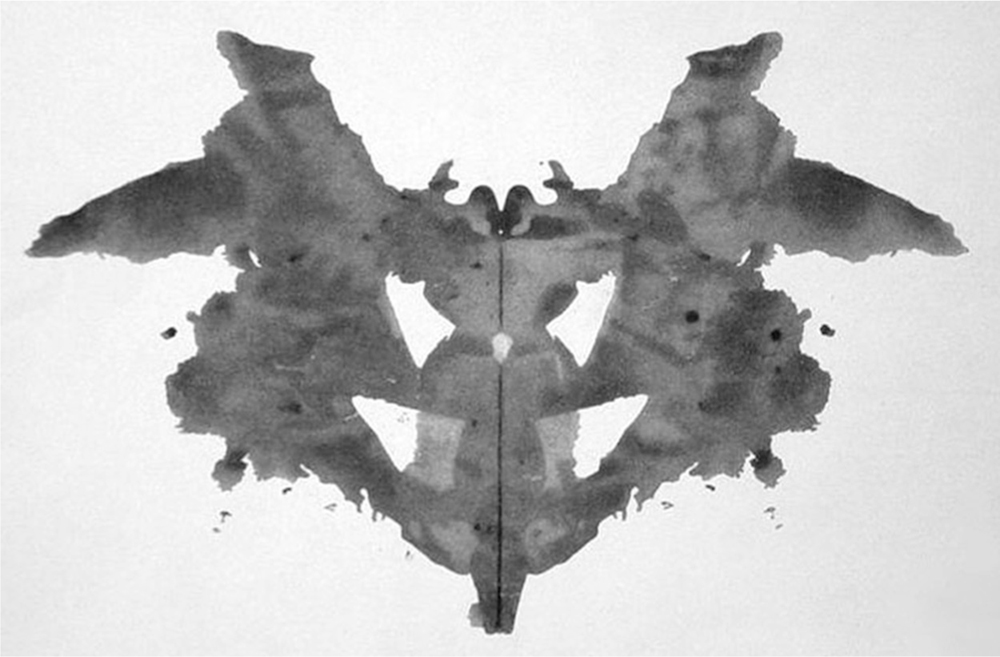
Fig. 1.2 A Rorschach inkblot test used to test for various personality disorders (originally a diagnostic tool for schizophrenia) and uncovering past, repressed traumas. What do you see? Most people see a bat in this example. But a variety of ‘interpretations’ are possible. Models and theories in science tend to be similarly multiply interpretable. [Image in the public domain]

What we are faced with in physics is not inkblots but mathematical structures of some kind. Just as with the Rorschach test different subjects will interpret the self-same blot in many and varied ways, so one and the same mathematical formalism can (very often) be understood in many different ways. But this isn’t a free for all: the ways one can interpret the formalism are highly constrained by the world (experience and experimental evidence) and by logical and mathematical consistency. However, even these tight constraints leave much elbow room, resulting in world-pictures entirely at odds with one another in all but empirical matters.

Given this feature, we see that ‘interpretation’ is a well-chosen term: in art we speak of “interpreting the painting” (usually when it is an abstract work). In music we speak of the performer as “interpreting the works of the great masters.” Implicit in this is the idea of a multiplicity of interpretive options. Also related to the ordinary-language sense of interpretation is that there must be some ‘closeness’ to the painting or musical score. You can’t very well give an interpretation of a Beethoven sonata without actually rendering sounds that are ‘isomorphic’ (that is, in one-to-one correspondence, or thereabouts) with the score (even if there are some wrong notes so that the isomorphism is partial, rather than a perfect correspondence). Different interpretations of a score will differ in some ways, but will have the same basic structure as supplied by the score, which supplies a kind of musical syntax akin to a mathematical formalism of a physical theory. Interpretations of physical theories can (must) be the same in some ways, while differing in other ways, just like musical interpretations.

Interpretation is also closely linked to ontology: to interpret is often just to provide an ontology. Bas van Fraassen describes the link as follows: “The question of interpretation [asks:] what would it be like for this theory to be true, and how could the world possibly be the way this theory says it is?” ([52], p. 242). The interpreter will then answer by specifying the class of possible worlds that make the theory true in the sense of satisfying the basic theoretical postulates (laws or axioms) - the musical performance analogy would state that interpretations of a piece of music (musical possible worlds) are those that satisfy the score. What we end up with, then, is a set of possible worlds that make the theory true; or, a set of possible worlds according to the theory (or at which the theory is true).

There are, then, two parts to an interpretation: a syntactic part (in which the formal structures and central axioms are laid out) and a semantic part providing the formal structures with ‘meaning’ (and in which the ‘possible worlds’ are specified, where these worlds are taken to be ‘models’ of the syntactic part). We would also have to consider some kind of ‘relevance condition’ as being involved in interpretation, since one could in principle interpret a formalism (or a score) in some way not intended: e.g. having a representation relation that maps musical scores to colors rather than sounds (or the wrong kinds of sounds: penny whistle rather than full orchestra), or a relation that maps a mathematical formalism to states of an abstract computer programme rather than a (real or possible) universe, or one of its subsystems. Once we have the interpretation, we can to a large extent ignore the physical world and focus on the interpreted theory itself, making discoveries in it that one would expect to find in the world - to test the theory will obviously require a comparison with observation and experiment, but it is likely true that most theoretical and mathematical physicists spend more time looking at a whiteboard or pad of paper (on which they construct and ‘explore’ some representation) than the very world that is their real target.

The multiplicity of interpretations is a blessing in the musical context: imagine how dull life would be if all performances sounded the same! But in the case of a mathematical formulation of a theory that admits multiple interpretations (different ways of filling in the semantics), we face a problem if we view our theories as telling us how the world is: these interpretations are supposed to be telling us how the world is, and yet they are usually incompatible. One interpretation might be local, so that there is no action-at-a-distance, while another interpretation (of the same theory) might be nonlocal. One might be deterministic, another indeterministic, and so on. They can’t all be viewed as gripping onto our world since there are contradictions involved. So here we have a striking dis-analogy with the musical case: we might prefer one performance over another, but we aren’t forced into believing in ‘the one true performance’ as we are with a theory that aims to provide a picture of reality. This possibility of several incompatible ontologies constitutes one of the thorniest epistemological problems faced by philosophers of science: the problem of underdetermination.

There is an additional level to the interpretation game that we have not yet mentioned. This is that the interpreted formalism can also be subject to further interpretation (and further multiplicity in interpretation). In other words, we view our object-to-be-interpreted not as a ‘bare formalism,’ but as an already-interpreted structure. For example, we might be studying the ‘many worlds’ interpretation of quantum mechanics (itself one of many observationally equivalent interpretations of the basic principles of quantum mechanics). We can ask of this interpreted formalism: what can the world be like for this to be true? Again, there might be multiplicity at this higher level, where supplying a semantics to the basic formalism is not enough to fix a world-picture (or all of its details). Are the many-worlds really to be viewed as separate universes that literally branch off from one another, or as something else not involving a literal branching of worlds? Likewise, with general relativity (Einstein’s theory of gravitation) where we understand it to be a theory of spacetime geometry, the question arises again: given this interpreted formalism (in terms of spacetime curvature), what is the world like? Is there a literal spacetime geometry in the world, as substantial as tables and chairs? Or is it somehow built up from tables and chairs, and other forms of mass-energy. How much of the spacetime geometry picture do we suppose maps onto the world: just the geometrical structure or the extensionless points underlying this structure too?

Sometimes we simply call the initially interpreted formalism the theory, rather than an interpretation. For example, to most people (physicists included) general relativity is just a theory about the curvature of spacetime geometry and the way the curvature depends on the goings on of matter and energy in the spacetime. But this is only one possible approach. A flat spacetime picture with gravity mediated by an ‘exchange particle’ (the graviton) can also rightly be called general relativity. Here, the dynamically varying metric tensor (representing the geometry of spacetime in the orthodox picture) is treated as ‘just another field in flat spacetime’ - there are technical details involved in recovering the same predictions and symmetry properties, but we need not concern ourselves with these. The point is, we can treat the theory as involving curved space or flat space; that we tend to work with one approach does nothing to detract from the fact that the curved space picture is also an interpretation of sorts.

1.4 Why Does Physics Work?

One of the most puzzling facts about physics is that it works! How do theories perform this amazing feat. Easy, you might say: they work because they’re true. But given the issue of multiplicity in interpretations of a theory (mentioned in the previous section), which picture is true? One often has very different ontologies (e.g. one with fields and one with particles instead; one with flat space, one with curved space instead, and so on). What concerns us here is why mathematics (an abstract thing, according to most) is able to predict and describe physical events. Why don’t crystal balls, tea leaves, or any number of other things work? At least they are physical entities!

This problem was famously posed by Eugene Wigner in 1960 in a paper called “The Unreasonable Effectiveness of Mathematics in the Natural Sciences.” He put the puzzle in strong terms: “the enormous usefulness of mathematics in the natural sciences is something bordering on the mysterious and that there is no rational explanation for it” ([56], 2). For example, there are branches of mathematics that allow us to predict the behaviors of planets, comets, missiles, and even certain elements of social systems, such as traffic flow patterns and queuing behavior. Why are the laws of physics so well-couched in the language of mathematics? Why do mathematical structures find such fruitful application in physics?

There are two kinds of application we can think of here, one more ‘unreasonable’ than the other: (1) a ‘physics-dependent’ kind, and (2) a ‘physics-independent’ kind. For example, there are cases where mathematics has been developed hand-in-hand with some piece of physics: the calculus was constructed with a physical problem in mind, namely how can we solve equations of motion (how do we know how a system will evolve in time). John von Neumann’s creation of Hilbert space (in which quantum states are represented) was also of this kind: a case of finding appropriate mathematical tools for the job. The effectiveness of mathematics is clearly not so unreasonable in such cases: it is a criterion of successful tool-finding that it be an effective one. There were many tools not fit for purpose that were discarded.

The unreasonable kind is that application of mathematics in science (Wigner has in mind physics, primarily, but it generalizes to any mathematically modeled subject matter) that was created independently of physics and yet later found application in physics. Hence, the mathematicians were busying themselves with some purely mathematical problem, not caring a jot about the world of physics, and yet lo and behold this piece of mathematics is found to be a perfect fit for (some aspect of) the physical world. For example, complex numbers find a perfect home in quantum mechanics, as we will see, despite the fact that complex numbers were developed hundreds of years before quantum mechanics was conceived. Non-Euclidean geometries were found to provide the perfect framework for general relativity. The so-called ‘spinors’ of Henri Cartan, from 1913, were found to fit perfectly the intrinsic spin of electrons discovered in 1926 (and were pivotal in the theoretical prediction of anti-matter by Paul Dirac, who combined spinors with the mathematics of quantum mechanics). Wigner’s own example involved a pair of old friends discussing one friend’s job as a statistician. The other friend is incredulous to see that π (something to do with the ratio of circumference of the circle to its diameter) is appearing in a discussion of the population (humans!) via the Gaussian distribution. How can this be?

There are various responses one could give. One possible response is that even the ‘purest’ (most physics-independent) mathematics comes from worldly investigations at some level, as Stanislaw Ulam points out:

Even the most idealistic point of view of mathematics as a pure creation of the human mind must be reconciled with the fact that the choice of definitions and axioms of geometry - in fact of most mathematical concepts - is the result of impressions obtained through our senses from external stimuli and inherently from observations and experiments in the ‘external world.’ ([51], p. 284)

This doesn’t really explain how mathematics can extend physics to go beyond what we can obtain through the senses: our senses are often wrong, and certainly can’t put us directly in touch with atoms and quarks.

Better, one might deflate the puzzle by showing how it is no more miraculous than finding, e.g. a piece of furniture that fits ‘just so’ into some space in a room - and to think, the manufacturer had no idea about my room! I don’t wish to suggest that mathematical physics is on a par with interior design, of course, but in terms of the basic principle behind the deployment of mathematics in physics, I think there are parallels here. But there is a crucial aspect left untreated: the furniture fits because the space has a structure with the right dimensions. It is a matching of (aspects of) their structures that grounds the fit. What about the case of mathematics and physics?

To answer this we might adopt the view that since mathematics is a science of patterns and structure and the world is patterned and structured, there is no mystery about their relationship: they simply have the same structure. Quite naturally, some structures will match up and others won’t: the unreasonable effectiveness then just amounts to finding isomorphic structures, and why should it matter that the mathematical structure was discovered before the physical structure? Further, in physics, one is often dealing with a very limited list of physical features to be represented mathematically, so a matching between them is not so far fetched.

On this view, when one has a match between some piece of mathematics and some aspect of physical reality, then one has made a discovery that the world has this mathematical structure. One can then perhaps explain why the mathematics can lead to surprising physical discoveries - situations where we appear to get more out of the mathematics than we put in, to use Wigner’s expression. A problem with this view is that sometimes mathematics is effective without us wanting to say that there is some structural isomorphism between the mathematics and the world. For example, we might have a model that would be physically inconsistent (such as the early model of the orbit of the electron around the nucleus, which predicted a rapid collapse of the atom) and so couldn’t possibly be matched by reality. There are also all sorts of ‘idealizations’ in physics in which the mathematical model and the world can’t be seen to correspond in terms of actual structure.

It is a good idea to keep in mind that we are dealing with scientific representations - most often (if not always) mathematical in the context of physics. The aim, as mentioned in the previous section, is to ‘mimic’ (or capture) in the representation the key (relevant, important) features of the system you are interested in (the target system). One can try to visualize what is going on in such modeling in fig. 1.3.

Here we start with a real-world system, and construct some model (which will neglect many of the details of our intended target in the world: transforming a real cow into a ‘spherical cow’ for simplicity, for example). We then deal with the model system and develop a theory of its behavior. The question is whether the theoretical representation describing the model also describes the worldly system - in terms of fig. 1.3, we ask whether the diagram commutes: must we go via the paired down model system, or can we use the representation directly for the worldly system? In terms of the success of mathematical representations, the miraculous quality concerns the fact that such representations often allow us to perform this ‘bypass operation,’ using the representation to describe and predict the behavior of various systems of interest, when the mathematics was developed in an entirely different context.5

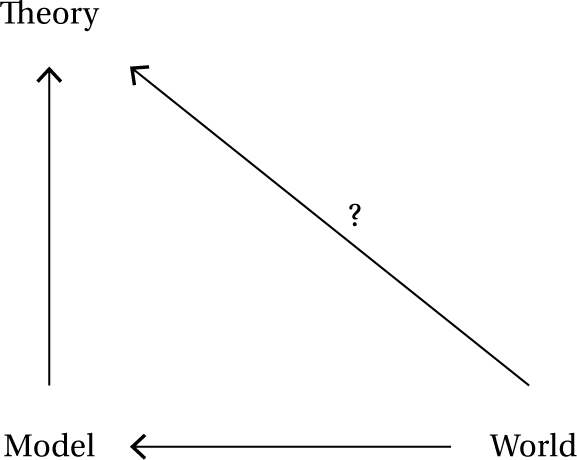
Fig. 1.3 A diagram making the problems of success (and failure) of the application of mathematics in the scientific enterprise a little more transparent. A real-world system is turned into a ‘model’ system (by abstracting away complex, unnecessary details), which is then involved in the theoretical description. If this phase is successful then we can view the theory as describing the real-world system. If not, then there may have been some problem in the model-building/ representation stage (perhaps an over-idealization), so that ‘Model’ and ‘World’ are too dissimilar (in some relevant way) for a theory about the model to apply to the real-world target.

1.5 Further Readings

There are several philosophy of physics textbooks that I warmly recommend, though some are pitched many levels up from the present book. Those that are pitched at roughly the same level, adopt different approaches, tackle different kinds of question, or are less general.

Fun

· Nick Huggett (2010) Everywhere and Everywhen: Adventures in Physics and Philosophy. Oxford University Press.
- This is a particularly sparkling treatment of several interesting themes in philosophy of physics, mostly focusing on space and time.

Serious

· Lawrence Sklar (2010) Philosophy of Physics. Oxford University Press.
- Still a very good philosophy of physics introduction, though starting to show its age a little.

· James Cushing (1998) Philosophical Concepts in Physics: The Historical Relation Between Philosophy and Scientific Theories. Cambridge University Press.
- Wonderfully wide-ranging discussion of the intersection of philosophy and physics (stretching back to ancient physics and advancing all the way to general relativity and quantum theory). A great way to get some history, physics, and philosophy in one place.

Connoisseurs

· Jeremy Butterfield and John Earman, eds. (2007) Handbook on the Philosophy of Physics. Elsevier.
- This represents a professional-level treatment of various subjects in philosophy of physics, written by a team of authors that includes physicists. Mastering the chapters of this volume should be something you aspire to!

· Robert Batterman, ed. (2013) The Oxford Handbook of Philosophy of Physics. Oxford University Press.
- This collection of new essays provides introductory treatments of more modern debates in philosophy of physics, including especially condensed matter and statistical physics. However, it includes very good chapters on quantum mechanics, spacetime, and other more standard topics.

Notes

1 There have been some interesting developments in the physics-philosophy ‘dialogue’ recently, showing that the question over the legitimacy of thinking philosophically about physics (and science in general) is still alive. Stephen Hawking declared (at Google’s ‘Zeitgeist’ Conference in 2011) that “philosophy is dead” on account of its detachment from actual, current science: philosophers just haven’t kept up with the science. A read through journals such as, e.g. Studies in the History and Philosophy of Modern Physics, will quickly reveal a very different story, with philosophers writing on subjects at the cutting edge (often in collaboration with physicists). A further problem with Hawking’s view is that he ignores the fact that a great many philosophical assumptions are buried in the work he (and other theoretical physicists) do, especially in terms of how mathematical structure is understood to map onto the world. Likewise, in his book A Universe from Nothing: Why there is Something Rather than Nothing (Atria Books, 2013), physicist Lawrence Krauss argued, following Feynman’s path, that philosophy is inert when it comes to physics: it doesn’t influence how physics works, nor does it progress like physics. In answering (he thinks) the most fundamental problem of philosophy (why there is something rather than nothing) using physics alone, he doesn’t see any elbow room left for philosophy to do its thing: even the deepest questions can be dealt with by physics. Philosopher of physics David Albert responded (in the New York Times, March 23, 2012) with a critique outlining how Krauss hadn’t answered this deep question at all, but an entirely differerent one: how can you get something from not quite nothing (i.e. something)! For example, it leaves completely untouched the question of where the laws of physics come from, and requires a quantum vacuum (very much a something). Read Krauss’ book, and see if you think he has answered the question satisfactorily.2 I’m sure historians of science would quibble with much that I have said here, finding earlier examples of laws of nature of sorts (e.g. Aristotle’s notion of ‘natural place’ guiding fire, water, and so on), or examples of early uses of instrumentation (e.g. the use of gnomons to chart the progression of the sun’s path) - see Daniel Graham’s Science Before Socrates (Oxford University Press, 2013) for just such a history. This might well be so, but the point I’m making is that the detachment of scientific knowledge from our unaided sense organs combined (or going hand in hand) with the increased mathematization of scientific knowledge provides fertile ground essential for doing modern philosophy of physics.3 I point the reader toward Wesley Salmon’s excellent collection Zeno’s Paradoxes (Hackett Publishing Company, 1970) for more examples and discussions.4 Readers interested in more details should consult Roman Frigg and Stephan Hartmann’s “Models in Science”: http://plato.stanford.edu/entries/models-science/.5 These are difficult issues, which we won’t pursue further in this book. However, Christopher Pincock provides an admirable overview and attempt at an explanation of the role played by mathematics in science in his book Mathematics and Scientific Representation (Oxford University Press, 2012). This is especially useful from the point of view of Wigner’s question since it also deals with failures of mathematical modeling in which there is too much distance between the model and reality (e.g. omitting or idealizing in such a way as to generate unphysical predictions in the theoretical description).