The Elegant Universe: Superstrings, Hidden Dimensions, and the Quest for the Ultimate Theory - Brian Greene (2010)

Part III. The Cosmic Symphony

Chapter 7. The "Super" in Superstrings

When the success of Eddington's 1919 expedition to measure Einstein's prediction of the bending of starlight by the sun had been established, the Dutch physicist Hendrik Lorentz sent Einstein a telegram informing him of the good news. As word of the telegram's confirmation of general relativity spread, a student asked Einstein about what he would have thought if Eddington's experiment had not found the predicted bending of starlight. Einstein replied, "Then I would have been sorry for the dear Lord, for the theory is correct."¹ Of course, had experiments truly failed to confirm Einstein's predictions, the theory would not be correct and general relativity would not have become a pillar of modern physics. But what Einstein meant is that general relativity describes gravity with such a deep inner elegance, with such simple yet powerful ideas, that he found it hard to imagine that nature could pass it by. General relativity, in Einstein's view, was almost too beautiful to be wrong.

Aesthetic judgments do not arbitrate scientific discourse, however. Ultimately, theories are judged by how they fare when faced with cold, hard, experimental facts. But this last remark is subject to an immensely important qualification. While a theory is being constructed, its incomplete state of development often prevents its detailed experimental consequences from being assessed. Nevertheless, physicists must make choices and exercise judgments about the research direction in which to take their partially completed theory. Some of these decisions are dictated by internal logical consistency; we certainly require that any sensible theory avoid logical absurdities. Other decisions are guided by a sense of the qualitative experimental implications of one theoretical construct relative to another; we are generally not interested in a theory if it has no capacity to resemble anything we encounter in the world around us. But it is certainly the case that some decisions made by theoretical physicists are founded upon an aesthetic sense—a sense of which theories have an elegance and beauty of structure on par with the world we experience. Of course, nothing ensures that this strategy leads to truth. Maybe, deep down, the universe has a less elegant structure than our experiences have led us to believe, or maybe we will find that our current aesthetic criteria need significant refining when applied in ever less familiar contexts. Nevertheless, especially as we enter an era in which our theories describe realms of the universe that are increasingly difficult to probe experimentally, physicists do rely on such an aesthetic to help them steer clear of blind alleys and dead-end roads that they might otherwise pursue. So far, this approach has provided a powerful and insightful guide.

In physics, as in art, symmetry is a key part of aesthetics. But unlike the case in art, symmetry in physics has a very concrete and precise meaning. In fact, by diligently following this precise notion of symmetry to its mathematical conclusion, physicists during the last few decades have found theories in which matter particles and messenger particles are far more closely intertwined than anyone previously thought possible. Such theories, which unite not only the forces of nature but also the material constituents, have the greatest possible symmetry and for this reason have been called supersymmetric. Superstring theory, as we shall see, is both the progenitor and the pinnacle example of a supersymmetric framework.

The Nature of Physical Law

Imagine a universe in which the laws of physics are as ephemeral as the tastes of fashion—changing from year to year, from week to week, or even from moment to moment. In such a world, assuming that the changes do not disrupt basic life processes, you would never experience a dull moment, to say the least. The simplest acts would be an adventure, since random variations would prevent you or anyone else from using past experience to predict anything about future outcomes.

Such a universe is a physicist's nightmare. Physicists—and most everyone else as well—rely crucially upon the stability of the universe: The laws that are true today were true yesterday and will still be true tomorrow (even if we have not been clever enough to have figured them all out). After all, what meaning can we give to the term "law" if it can abruptly change? This does not mean that the universe is static; the universe certainly changes in innumerable ways from each moment to the next. Rather, it means that the laws governing such evolution are fixed and unchanging. You might ask whether we really know this to be true. In fact, we don't. But our success in describing numerous features of the universe, from a brief moment after the big bang right through to the present, assures us that if the laws are changing they must be doing so very slowly. The simplest assumption that is consistent with all that we know is that the laws are fixed.

Now imagine a universe in which the laws of physics are as parochial as local culture—changing unpredictably from place to place and defiantly resisting any outside influence to conform. Like the adventures of Gulliver, travels in such a world would expose you to an enormously rich array of unpredictable experiences. But from a physicist's perspective, this is yet another nightmare. It's hard enough, for instance, to live with the fact that laws that are valid in one country—or even one state—may not be valid in another. But imagine what things would be like if the laws of nature were as varied. In such a world experiments carried out in one locale would have no bearing on the physical laws relevant somewhere else. Instead, physicists would have to redo experiments over and over again in different locations to probe the local laws of nature that hold in each. Thankfully, everything we know points toward the laws of physics being the same everywhere. All experiments the world over converge on the same set of underlying physical explanations. Moreover, our ability to explain a vast number of astrophysical observations of far-flung regions of the cosmos using one, fixed set of physical principles leads us to believe that the same laws do hold true everywhere. Having never traveled to the opposite end of the universe, we can't definitively rule out the possibility that a whole new kind of physics prevails elsewhere, but everything points to the contrary.

Again, this does not mean that the universe looks the same—or has the same detailed properties—in different locations. An astronaut jumping on a pogo stick on the moon can do all sorts of things that are impossible to do on earth. But we recognize that the difference arises because the moon is far less massive than the earth; it does not mean that the law of gravity is somehow changing from place to place. Newton's, or more precisely, Einstein's, law of gravity is the same on earth as it is on the moon. The difference in the astronaut's experience is one of change in environmental detail, not variation of physical law.

Physicists describe these two properties of physical laws—that they do not depend on when or where you use them—as symmetries of nature. By this usage physicists mean that nature treats every moment in time and every location in space identically—symmetrically—by ensuring that the same fundamental laws are in operation. Much in the same manner that they affect art and music, such symmetries are deeply satisfying; they highlight an order and a coherence in the workings of nature. The elegance of rich, complex, and diverse phenomena emerging from a simple set of universal laws is at least part of what physicists mean when they invoke the term "beautiful."

In our discussions of the special and general theories of relativity, we came upon yet other symmetries of nature. Recall that the principle of relativity, which lies at the heart of special relativity, tells us that all physical laws must be the same regardless of the constant-velocity relative motion that individual observers might experience. This is a symmetry because it means that nature treats all such observers identically—symmetrically. Each such observer is justified in considering himself or herself to be at rest. Again, it's not that observers in relative motion will make identical observations; as we have seen earlier, there are all sorts of stunning differences in their observations. Instead, like the disparate experiences of the pogo-stick enthusiast on the earth and on the moon, the differences in observations reflect environmental details—the observers are in relative motion—even though their observations are governed by identical laws.

Through the equivalence principle of general relativity, Einstein significantly extended this symmetry by showing that the laws of physics are actually identical for all observers, even if they are undergoing complicated accelerated motion. Recall that Einstein accomplished this by realizing that an accelerated observer is also perfectly justified in declaring himself or herself to be at rest, and in claiming that the force he or she feels is due to a gravitational field. Once gravity is included in the framework, all possible observational vantage points are on a completely equal footing. Beyond the intrinsic aesthetic appeal of this egalitarian treatment of all motion, we have seen that these symmetry principles played a pivotal role in the stunning conclusions regarding gravity that Einstein found.

Are there any other symmetry principles having to do with space, time, and motion that the laws of nature should respect? If you think about this you might come up with one more possibility. The laws of physics should not care about the angle from which you make your observations. For instance, if you perform some experiment and then decide to rotate all of your equipment and do the experiment again, the same laws should apply. This is known as rotational symmetry, and it means that the laws of physics treat all possible orientations on equal footing. It is a symmetry principle that is on par with the previous ones discussed.

Are there others? Have we overlooked any symmetries? You might suggest the gauge symmetries associated with the nongravitational forces, as discussed in Chapter 5. These are certainly symmetries of nature, but they are of a more abstract sort; our focus here is on symmetries that have a direct link to space, time, or motion. With this stipulation, it's now likely that you can't think of any other possibilities. In fact, in 1967 physicists Sidney Coleman and Jeffrey Mandula were able to prove that no other symmetries associated with space, time, or motion could be combined with those just discussed and result in a theory bearing any resemblance to our world.

Subsequently, though, close examination of this theorem, based on insights of a number of physicists revealed precisely one subtle loophole: The Coleman-Mandula result did not exploit fully symmetries sensitive to something known as spin.

Spin

An elementary particle such as an electron can orbit an atomic nucleus in somewhat the same way that the earth orbits the sun. But, in the traditional point-particle description of an electron, it would appear that there is no analog of the earth's spinning around on its axis. When any object spins, points on the axis of rotation itself—like the central point of a spinning Frisbee—do not move. If something is truly pointlike, though, it has no "other points" that lie off of any purported spin axis. And so it would appear that there simply is no notion of a point object spinning. Many years ago, such reasoning fell prey to yet another quantum-mechanical surprise.

In 1925, the Dutch physicists George Uhlenbeck and Samuel Goudsmit realized that a wealth of puzzling data having to do with properties of light emitted and absorbed by atoms could be explained if electrons were assumed to have very particular magnetic properties. Some hundred years earlier, the Frenchman Andre-Marie Ampère had shown that magnetism arises from the motion of electric charge. Uhlenbeck and Goudsmit followed this lead and found that only one specific sort of electron motion could give rise to the magnetic properties suggested by the data: rotational motion—that is, spin. Contrary to classical expectations, Uhlenbeck and Goudsmit proclaimed that, somewhat like the earth, electrons both revolve and rotate.

Did Uhlenbeck and Goudsmit literally mean that the electron is spinning? Yes and no. What their work really showed is that there is a quantum-mechanical notion of spin that is somewhat akin to the usual image but inherently quantum mechanical in nature. It's one of those properties of the microscopic world that brushes up against classical ideas but injects an experimentally verified quantum twist. For instance, picture a spinning skater. As she pulls her arms in she spins more quickly; as she stretches out her arms she spins more slowly. And sooner or later, depending on how vigorously she threw herself into the spin, she will slow down and stop. Not so for the kind of spin revealed by Uhlenbeck and Goudsmit. According to their work and subsequent studies, every electron in the universe, always and forever, spins at one fixed and never changing rate. The spin of an electron is not a transitory state of motion as for more familiar objects that, for some reason or other, happen to be spinning. Instead, the spin of an electron is an intrinsic property, much like its mass or its electric charge. If an electron were not spinning, it would not be an electron.

Although early work focused on the electron, physicists have subsequently shown that these ideas about spin apply equally well to all of the matter particles that fill out the three families of Table 1.1. This is true down to the last detail: All of the matter particles (and their antimatter partners as well) have spin equal to that of the electron. In the language of the trade, physicists say that matter particles all have "spin-1/2," where the value 1/2 is, roughly speaking, a quantum-mechanical measure of how quickly the particles rotate.² Moreover, physicists have shown that the nongravitational force carriers—photons, weak gauge bosons, and gluons—also possess an intrinsic spinning characteristic that turns out to be twice that of the matter particles. They all have "spin-1."

What about gravity? Well, even before string theory, physicists were able to determine what spin the hypothesized graviton must have to be the transmitter of the gravitational force. The answer: twice the spin of photons, weak gauge bosons, and gluons—i.e., "spin-2."

In the context of string theory, spin—just like mass and force charges—is associated with the pattern of vibration that a string executes. As with point particles, it's a bit misleading to think of the spin carried by a string as arising from its spinning literally around in space, but this image does give a loose picture to have in mind. By the way, we can now clarify an important issue we encountered earlier. In 1974, when Scherk and Schwarz proclaimed that string theory should be thought of as a quantum theory incorporating the gravitational force, they did so because they had found that strings necessarily have a vibrational pattern in their repertoire that is massless and has spin-2—the hallmark features of the graviton. Where there is a graviton there is also gravity.

With this background on the concept of spin, let's now turn to the role it plays in revealing the loophole in the Coleman-Mandula result concerning the possible symmetries of nature, mentioned in the preceding section.

Supersymmetry and Superpartners

As we have emphasized, the concept of spin, although superficially akin to the image of a spinning top, differs in substantial ways that are rooted in quantum mechanics. Its discovery in 1925 revealed that there is another kind of rotational motion that simply would not exist in a purely classical universe.

This suggests the following question: Just as ordinary rotational motion allows for the symmetry principle of rotational invariance ("physics treats all spatial orientations on an equal footing"), could it be that the more subtle rotational motion associated with spin leads to another possible symmetry of the laws of nature? By 1971 or so, physicists showed that the answer to this question was yes. Although the full story is quite involved, the basic idea is that when spin is considered, there is precisely one more symmetry of the laws of nature that is mathematically possible. It is known as supersymmetry.³

Supersymmetry cannot be associated with a simple and intuitive change in observational vantage point; shifts in time, in spatial location, in angular orientation, and in velocity of motion exhaust these possibilities. But just as spin is "like rotational motion, with a quantum-mechanical twist," supersymmetry can be associated with a change in observational vantage point in a "quantum-mechanical extension of space and time." These quotes are especially important, as the last sentence is only meant to give a rough sense of where supersymmetry fits into the larger framework of symmetry principles.⁴ Nevertheless, although understanding the origin of supersymmetry is rather subtle, we will focus on one of its primary implications—should the laws of nature incorporate its principles—and this is far easier to grasp.

In the early 1970s, physicists realized that if the universe is supersymmetric, the particles of nature must come in pairs whose respective spins differ by half a unit. Such pairs of particles—regardless of whether they are thought of as pointlike (as in the standard model) or as tiny vibrating loops—are called superpartners. Since matter particles have spin-1/2 while some of the messenger particles have spin-1, supersymmetry appears to result in a pairing—a partnering—of matter and force particles. As such, it seems like a wonderful unifying concept. The problem comes in the details.

By the mid-1970s, when physicists sought to incorporate supersymmetry into the standard model, they found that none of the known particles—those of Tables 1.1 and 1.2—could be superpartners of one another. Instead, detailed theoretical analysis showed that if the universe incorporates supersymmetry, then every known particle must have an as-yet-undiscovered superpartner particle, whose spin is half a unit less than its known counterpart. For instance, there should be a spin-0 partner of the electron; this hypothetical particle has been named the selectron (a contraction of supersymmetric-electron). The same should also be true for the other matter particles, with, for example, the hypothetical spin-0 superpartners of neutrinos and quarks being called sneutrinos and squarks. Similarly, the force particles should have spin-1/2 superpartners: For photons there should be photinos, for the gluons there should be gluinos, for the W and Z bosons there should be winos and zinos.

On closer inspection, then, supersymmetry seems to be a terribly uneconomical feature; it requires a whole slew of additional particles that wind up doubling the list of fundamental ingredients. Since none of the superpartner particles has ever been detected, you would be justified to take Rabi's remark from Chapter 1 regarding the discovery of the muon one step further, declare that "nobody ordered supersymmetry," and summarily reject this symmetry principle. For three reasons, however, many physicists believe strongly that such an out-of-hand dismissal of supersymmetry would be quite premature. Let's discuss these reasons.

The Case for Supersymmetry: Prior to String Theory

First, from an aesthetic standpoint, physicists find it hard to believe that nature would respect almost, but not quite all of the symmetries that are mathematically possible. Of course, it is possible that an incomplete utilization of symmetry is what actually occurs, but it would be such a shame. It would be as if Bach, after developing numerous intertwining voices to fill out an ingenious pattern of musical symmetry, left out the final, resolving measure.

Second, even within the standard model, a theory that ignores gravity, thorny technical issues that are associated with quantum processes are swiftly solved if the theory is supersymmetric. The basic problem is that every distinct particle species makes its own contribution to the microscopic quantum-mechanical frenzy. Physicists have found that in the bath of this frenzy, certain processes involving particle interactions remain consistent only if numerical parameters in the standard model are fine-tuned—to better than one part in a million billion—to cancel out the most pernicious quantum effects. Such precision is on par with adjusting the launch angle of a bullet fired from an enormously powerful rifle, so that it hits a specified target on the moon with a margin of error no greater than the thickness of an amoeba. Although numerical adjustments of an analogous precision can be made within the standard model, many physicists are quite suspect of a theory that is so delicately constructed that it falls apart if a number on which it depends is changed in the fifteenth digit after the decimal point.⁵

Supersymmetry changes this drastically because bosons—particles whose spin is a whole number (named after the Indian physicist Satyendra Bose)—and fermions—particles whose spin is half of a whole (odd) number (named after the Italian physicist Enrico Fermi)—tend to give cancelling quantum-mechanical contributions. Like opposite ends of a seesaw, when the quantum jitters of a boson are positive, those of a fermion tend to be negative, and vice versa. Since supersymmetry ensures that bosons and fermions occur in pairs, substantial cancellations occur from the outset—cancellations that significantly calm some of the frenzied quantum effects. It turns out that the consistency of the supersymmetric standard model—the standard model augmented by all of the superpartner particles—no longer relies upon the uncomfortably delicate numerical adjustments of the ordinary standard model. Although this is a highly technical issue, many particle physicists find that this realization makes supersymmetry very attractive.

The third piece of circumstantial evidence for supersymmetry comes from the notion of grand unification. One of the puzzling features of nature's four forces is the huge range in their intrinsic strengths. The electromagnetic force has less than 1 percent of the strength of the strong force, the weak force is some thousand times feebler than that, and the gravitational force is some hundred million billion billion billion (10^-35) times weaker still. Following the pathbreaking and ultimately Nobel Prize-winning work of Glashow, Salam, and Weinberg that established a deep connection between the electromagnetic and weak forces (discussed in Chapter 5), in 1974 Glashow, together with his Harvard colleague Howard Georgi, suggested that an analogous connection might be forged with the strong force. Their work, which proposed a "grand unification" of three of the four forces, differed in one essential way from that of the electroweak theory: Whereas the electromagnetic and weak forces crystallized out of a more symmetric union when the temperature of the universe dropped to about a million billion degrees above absolute zero (10¹⁵ Kelvin), Georgi and Glashow showed that the union with the strong force would have been apparent only at a temperature some ten trillion times higher—around ten billion billion billion degrees above absolute zero (10²⁸ Kelvin). From the point of view of energy, this is about a million billion times the mass of the proton, or about four orders of magnitude less than the Planck mass. Georgi and Glashow boldly took theoretical physics into an energy realm many orders of magnitude beyond that which anyone had previously dared explore.

Subsequent work at Harvard by Georgi, Helen Quinn, and Weinberg in 1974 made the potential unity of the nongravitational forces within the grand unified framework even more manifest. As their contribution continues to play an important role in unifying the forces and in assessing the relevance of supersymmetry to the natural world, let's spend a moment explaining it.

We are all aware that the electrical attraction between two oppositely charged particles or the gravitational attraction between two massive bodies gets stronger as the distance between the objects decreases. These are simple and well-known features of classical physics. There is a surprise, though, when we study the effect that quantum physics has on force strengths. Why should quantum mechanics have any effect at all? The answer, once again, lies in quantum fluctuations. When we examine the electric force field of an electron, for example, we are actually examining it through the "mist" of momentary particle-antiparticle eruptions and annihilations that are occurring all through the region of space surrounding it. Physicists some time ago realized that this seething mist of microscopic fluctuations obscures the full strength of the electron's force field, somewhat as a thin fog partially obscures the beacon of a lighthouse. But notice that as we get closer to the electron, we will have penetrated more of the cloaking particle-antiparticle mist and hence will be less subject to its diminishing influence. This implies that the strength of an electron's electric field will increase as we get closer to it.

Physicists distinguish this quantum-mechanical increase in strength as we get closer to the electron from that known in classical physics by saying that the intrinsic strength of the electromagnetic force increases on shorter distance scales. This reflects that the strength increases not merely because we are closer to the electron but also because more of the electron's intrinsic electric field becomes visible. In fact, although we have focused on the electron, this discussion applies equally well to all electrically charged particles and is summarized by saying that quantum effects drive the strength of the electromagnetic force to get larger when examined on shorter distance scales.

What about the other forces of the standard model? How do their intrinsic strengths vary with distance? In 1973, Gross and Frank Wilczek at Princeton, and, independently, David Politzer at Harvard, studied this question and found a surprising answer: The quantum cloud of particle eruptions and annihilations amplifies the strengths of the strong and weak forces. This implies that as we examine them on shorter distances, we penetrate more of this seething cloud and hence are subject to less of its amplification. And so, the strengths of these forces get weaker when they are probed on shorter distances.

Georgi, Quinn, and Weinberg took this realization and ran with it to a remarkable end. They showed that when these effects of the quantum frenzy are carefully accounted for, the net result is that the strengths of all three nongravitational forces are driven together. Whereas the strengths of these forces are very different on scales accessible to current technology, Georgi, Quinn, and Weinberg argued that this difference is actually due to the different effect that the haze of microscopic quantum activity has on each force. Their calculations showed that if this haze is penetrated by examining the forces not on everyday scales but as they act on distances of about a hundredth of a billionth of a billionth of a billionth (10^-29) of a centimeter (a mere factor of ten thousand larger than the Planck length), the three nongravitational force strengths appear to become equal.

Although far removed from the realm of common experience, the high energy necessary to be sensitive to such small distances was characteristic of the roiling, hot early universe when it was about a thousandth of a trillionth of a trillionth of a trillionth (10^-39) of a second old—when its temperature was on the order of 10²⁸ Kelvin mentioned earlier. In somewhat the same way that a collection of disparate ingredients—pieces of metal, wood, rocks, minerals, and so on—all melt together and become a uniform, homogeneous plasma when heated to sufficiently high temperature, these theoretical works suggested that the strong, weak, and electromagnetic forces all merge into one grand force at such immense temperatures. This is shown schematically in Figure 7.1.⁶

Although we do not have the technology to probe such minute distance scales or to produce such scorching temperatures, since 1974 experimentalists have significantly refined the measured strengths of the three nongravitational forces under everyday conditions. These data—the starting points for the three force-strength curves in Figure 7.1—are the input data for the quantum-mechanical extrapolations of Georgi, Quinn, and Weinberg. In 1991, Ugo Amaldi of CERN, Wim de Boer and Hermann Fürstenau of the University of Karlsruhe, Germany, recalculated the Georgi, Quinn, and Weinberg extrapolations making use of these experimental refinements and showed two significant things. First, the strengths of the three nongravitational forces almost agree, but not quite at tiny distance scales (equivalently, high energy/high temperature) as shown in Figure 7.2. Second, this tiny but undeniable discrepancy in their strengths vanishes if supersymmetry is incorporated. The reason is that the new superpartner particles required by supersymmetry contribute additional quantum fluctuations, and these fluctuations are just right to nudge the strengths of the forces to converge with one another.

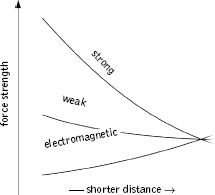
Figure 7.1 The strengths of the three nongravitational forces as they operate on ever shorter distance scales—equivalently, as they act on ever higher energy processes.

To many physicists, it is extremely difficult to believe that nature would choose the forces so that they almost, but not quite, have strengths that microscopically unify—microscopically become equal. It's like putting together a jigsaw puzzle in which the final piece is slightly misshapen and won't cleanly fit into its appointed position. Supersymmetry deftly refines its shape so that all pieces firmly lock into place.

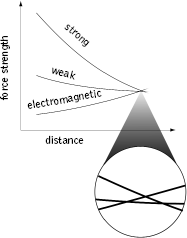
Figure 7.2 A refinement of the calculation of force strengths reveals that without supersymmetry they almost, but not quite, meet.

Another aspect of this latter realization is that it provides a possible answer to the question, Why haven't we discovered any of the superpartner particles? The calculations that lead to the convergence of the force strengths, as well as other considerations studied by a number of physicists, indicate that the superpartner particles must be a good deal heavier than the known particles. Although no definitive predictions can be made, studies show that the superpartner particles might be a thousand times as massive as a proton, if not heavier. As even our state-of-the-art accelerators cannot quite reach such energies, this provides an explanation for why these particles have not, as yet, been discovered. In Chapter 9, we will return to a discussion of the experimental prospects for determining in the near future whether supersymmetry truly is a property of our world.

Of course, the reasons we have given for believing in—or at least not yet rejecting—supersymmetry are far from airtight. We have described how supersymmetry elevates our theories to their most symmetric form—but you might suggest that the universe does not care about attaining the most symmetric form that is mathematically possible. We have noted the important technical point that supersymmetry relieves us from the delicate task of tuning numerical parameters in the standard model to avoid subtle quantum problems—but you might argue that the true theory describing nature may very well walk the fine edge between self-consistency and self-destruction. We have discussed how supersymmetry modifies the intrinsic strengths of the three nongravitational forces at tiny distances in just the right way for them to merge together into a grand unified force—but you might argue, again, that nothing in the design of nature dictates that these force strengths must exactly match on microscopic scales. And finally, you might suggest that a simpler explanation for why the superpartner particles have never been found is that our universe is not supersymmetric and, therefore, the superpartners do not exist.

No one can refute any of these responses. But the case for supersymmetry is strengthened immensely when we consider its role in string theory.

Supersymmetry in String Theory

The original string theory that emerged from Veneziano's work in the late 1960s incorporated all of the symmetries discussed at the beginning of this chapter, but it did not incorporate supersymmetry (which had not yet been discovered). This first theory based on the string concept was, more precisely, called the bosonic string theory. The name bosonic indicates that all of the vibrational patterns of the bosonic string have spins that are a whole number—there are no fermionic patterns, that is, no patterns with spins differing from a whole number by a half unit. This led to two problems.

First, if string theory was to describe all forces and all matter, it would somehow have to incorporate fermionic vibrational patterns, since the known matter particles all have spin-1/2. Second, and far more troubling, was the realization that there was one pattern of vibration in bosonic string theory whose mass (more precisely, whose mass squared) was negative—a so-called tachyon. Even before string theory, physicists had studied the possibility that our world might have tachyon particles, in addition to the familiar particles that all have positive masses, but their efforts showed that it is difficult if not impossible for such a theory to be logically sensible. Similarly, in the context of bosonic string theory, physicists tried all sorts of fancy footwork to make sense of the bizarre prediction of a tachyon vibrational pattern, but to no avail. These features made it increasingly clear that although it was an interesting theory, the bosonic string was missing something essential.

In 1971, Pierre Ramond of the University of Florida took up the challenge of modifying the bosonic string theory to include fermionic patterns of vibration. Through his work and subsequent results of Schwarz and Andre Neveu, a new version of string theory began to emerge. And much to everyone's surprise, the bosonic and the fermionic patterns of vibration of this new theory appeared to come in pairs. For each bosonic pattern there was a fermionic pattern, and vice versa. By 1977, insights of Ferdinando Gliozzi of the University of Turin, Scherk, and David Olive of Imperial College put this pairing into the proper light. The new string theory incorporated supersymmetry, and the observed pairing of bosonic and fermionic vibrational patterns reflected this highly symmetric character. Supersymmetric string theory—superstring theory, that is—had been born. Moreover, the work of Gliozzi, Scherk, and Olive had one other crucial result: They showed that the troublesome tachyon vibration of the bosonic string does not afflict the superstring. Slowly, the pieces of the string puzzle were falling into place.

Nevertheless, the major initial impact of the work of Ramond, and also of Neveu and Schwarz, was not actually in string theory. By 1973, the physicists Julius Wess and Bruno Zumino realized that supersymmetry—the new symmetry emerging from the reformulation of string theory—was applicable even to theories based on point particles. They rapidly made important strides toward incorporating supersymmetry into the framework of point-particle quantum field theory. And since, at the time, quantum field theory was the central rage of the mainstream particle-physics community—with string theory increasingly becoming a subject on the fringe—the insights of Wess and Zumino launched a tremendous amount of subsequent research on what has come to be called supersymmetric quantum field theory. The supersymmetric standard model, discussed in the preceding section, is one of the crowning theoretical achievements of these pursuits; we now see that, through historical twists and turns, even this point-particle theory owes a great debt to string theory.

With the resurgence of superstring theory in the mid-1980s, supersymmetry has re-emerged in the context of its original discovery. And in this framework, the case for supersymmetry goes well beyond that presented in the preceding section. String theory is the only way we know of to merge general relativity and quantum mechanics. But it's only the supersymmetric version of string theory that avoids the pernicious tachyon problem and that has fermionic vibrational patterns that can account for the matter particles constituting the world around us. Supersymmetry therefore comes hand-in-hand with string theory's proposal for a quantum theory of gravity, as well as with its grand claim of uniting all forces and all of matter. If string theory is right, physicists expect that so is supersymmetry.

Until the mid-1990s, however, one particularly troublesome aspect plagued supersymmetric string theory.

A Super-Embarrassment of Riches

If someone tells you that they have solved the mystery of Amelia Earhart's fate, you might be skeptical at first, but if they have a well-documented, thoroughly pondered explanation, you would probably hear them out and, who knows, you might even be convinced. But what if, in the next breath, they tell you that they actually have a second explanation as well. You listen patiently and are surprised to find the alternate explanation to be as well documented and thought through as the first. And after finishing the second explanation, you are presented with a third, a fourth, and even a fifth explanation—each different from the others and yet equally convincing. No doubt, by the end of the experience you would feel no closer to Amelia Earhart's true fate than you did at the outset. In the arena of fundamental explanations, more is definitely less.

By 1985, string theory—notwithstanding the justified excitement it was engendering—was starting to sound like our overzealous Earhart expert. The reason is that by 1985 physicists realized that supersymmetry, by then a central element in the structure of string theory, could actually be incorporated into string theory in not one but five different ways. Each method results in a pairing of bosonic and fermionic vibrational patterns, but the details of this pairing as well as numerous other properties of the resulting theories differ substantially. Although their names are not all that important, it's worth recording that these five supersymmetric string theories are called the Type I theory, the Type IIA theory, the Type IIB theory, the Heterotic type O(32) theory (pronounced "oh-thirty-two"), and the Heterotic type E₈ × E₈theory (pronounced "e-eight times e-eight"). All the features of string theory that we have discussed to this point are valid for each of these theories—they differ only in the finer details.

Having five different versions of what is supposedly the T.O.E.—possibly the ultimate unified theory—was quite an embarrassment for string theorists. Just as there is only one true explanation for whatever happened to Amelia Earhart (regardless of whether we will ever find it), we expect the same to be true regarding the deepest, most fundamental understanding of how the world works. We live in one universe; we expect one explanation.

One suggestion for resolving this problem might be that although there are five different superstring theories, four might be ruled out simply by experiment, leaving one true and relevant explanatory framework. But even if this were the case, we would still be left with the nagging question of why the other theories exist in the first place. In the wry words of Witten, "If one of the five theories describes our universe, who lives in the other four worlds?"⁷ A physicist's dream is that the search for the ultimate answers will lead to a single, unique, absolutely inevitable conclusion. Ideally, the final theory—whether string theory or something else—should be the way it is because there simply is no other possibility. If we were to discover that there is only one logically sound theory incorporating the basic ingredients of relativity and quantum mechanics, many feel that we would have reached the deepest understanding of why the universe has the properties it does. In short, this would be unified-theory paradise.⁸

As we will see in Chapter 12, recent research has taken superstring theory one giant step closer to this unified utopia by showing that the five different theories are, remarkably, actually five different ways of describing one and the same overarching theory. Superstring theory has the uniqueness pedigree.

Things seem to be falling into place, but, as we will discuss in the next chapter, unification through string theory does require one more significant departure from conventional wisdom.