The Elegant Universe: Superstrings, Hidden Dimensions, and the Quest for the Ultimate Theory - Brian Greene (2010)
Part III. The Cosmic Symphony
Chapter 6. Nothing but Music: The Essentials of Superstring Theory
Music has long since provided the metaphors of choice for those puzzling over questions of cosmic concern. From the ancient Pythagorean "music of the spheres" to the "harmonies of nature" that have guided inquiry through the ages, we have collectively sought the song of nature in the gentle wanderings of celestial bodies and the riotous fulminations of subatomic particles. With the discovery of superstring theory, musical metaphors take on a startling reality, for the theory suggests that the microscopic landscape is suffused with tiny strings whose vibrational patterns orchestrate the evolution of the cosmos. The winds of change, according to superstring theory, gust through an aeolian universe.
By contrast, the standard model views the elementary constituents of the universe as pointlike ingredients with no internal structure. As powerful as this approach is (as we have mentioned, essentially every prediction about the microworld made by the standard model has been verified down to about a billionth of a billionth of a meter, the present-day technological limit), the standard model cannot be a complete or final theory because it does not include gravity. Moreover, attempts to incorporate gravity into its quantum-mechanical framework have failed due to the violent fluctuations in the spatial fabric that appear at ultramicroscopic distances—that is, distances shorter than the Planck length. The unresolved conflict has impelled a search for an even deeper understanding of nature. In 1984, the physicists Michael Green, then of Queen Mary College, and John Schwarz of the California Institute of Technology provided the first piece of convincing evidence that superstring theory (or string theory, for short) might well provide this understanding.
String theory offers a novel and profound modification to our theoretical description of the ultramicroscopic properties of the universe—a modification that, physicists slowly realized, alters Einstein's general relativity in just the right way to make it fully compatible with the laws of quantum mechanics. According to string theory, the elementary ingredients of the universe are not point particles. Rather, they are tiny, one-dimensional filaments somewhat like infinitely thin rubber bands, vibrating to and fro. But don't let the name fool you: Unlike an ordinary piece of string, which is itself composed of molecules and atoms, the strings of string theory are purported to lie deep within the heart of matter. The theory proposes that they are ultramicroscopic ingredients making up the particles out of which atoms themselves are made. The strings of string theory are so small—on average they are about as long as the Planck length—that they appear pointlike even when examined with our most powerful equipment.
Yet the simple replacement of point particles with strands of string as the fundamental ingredients of everything has far-reaching consequences. First and foremost, string theory appears to resolve the conflict between general relativity and quantum mechanics. As we shall see, the spatially extended nature of a string is the crucial new element allowing for a single harmonious framework incorporating both theories. Second, string theory provides a truly unified theory, since all matter and all forces are proposed to arise from one basic ingredient: oscillating strings. Finally, as discussed more fully in subsequent chapters, beyond these remarkable achievements, string theory once again radically changes our understanding of spacetime.1
A Brief History of String Theory
In 1968, a young theoretical physicist named Gabriele Veneziano was struggling to make sense of various experimentally observed properties of the strong nuclear force. Veneziano, then a research fellow at CERN, the European accelerator laboratory in Geneva, Switzerland, had worked on aspects of this problem for a number of years, until one day he came upon a striking revelation. Much to his surprise, he realized that an esoteric formula concocted for purely mathematical pursuits by the renowned Swiss mathematician Leonhard Euler some two hundred years earlier—the so-called Euler beta-function—seemed to describe numerous properties of strongly interacting particles in one fell swoop. Veneziano's observation provided a powerful mathematical encapsulation of many features of the strong force and it launched an intense flurry of research aimed at using Euler's beta-function, and various generalizations, to describe the surfeit of data being collected at various atom smashers around the world. Nevertheless, there was a sense in which Veneziano's observation was incomplete. Like memorized formulae used by a student who does not understand their meaning or justification, Euler's beta-function seemed to work, but no one knew why. It was a formula in search of an explanation. This changed in 1970 when the works of Yoichiro Nambu of the University of Chicago, Holger Nielsen of the Niels Bohr Institute, and Leonard Susskind of Stanford University revealed the hitherto-unknown physics lurking behind Euler's formula. These physicists showed that if one modeled elementary particles as little, vibrating, one-dimensional strings, their nuclear interactions could be described exactly by Euler's function. If the pieces of string were small enough, they reasoned, they would still look like point particles, and hence could be consistent with experimental observations.
Although this provided an intuitively simple and pleasing theory, it was not long before the string description of the strong force was shown to fail. During the early 1970s, high-energy experiments capable of probing the subatomic world more deeply showed that the string model made a number of predictions that were in direct conflict with observations. At the same time, the point-particle quantum field theory of quantum chromodynamics was being developed, and its overwhelming success in describing the strong force led to the dismissal of string theory.
Most particle physicists thought that string theory had been relegated to the dustbin of science, but a few dedicated researchers kept at it. Schwarz, for instance, felt that "the mathematical structure of string theory was so beautiful and had so many miraculous properties that it had to be pointing toward something deep."2 One of the problems physicists found with string theory was that it seemed to have a true embarrassment of riches. The theory contained configurations of vibrating string that had properties akin to those of gluons, substantiating its early claim of being a theory of the strong force. But beyond these it contained additional messenger-like particles that did not appear to have any relevance to experimental observations of the strong force. In 1974, Schwarz and Joël Scherk of the Ecole Normale Superieure made a bold leap that transformed this apparent vice into a virtue. After studying the puzzling messenger-like patterns of string vibration, they realized that their properties matched perfectly those of the hypothesized messenger particle of the gravitational force—the graviton. Although these "smallest bundles" of the gravitational force have, as yet, never been seen, theorists can confidently predict certain basic features that they must possess, and Scherk and Schwarz found these properties to be realized exactly by certain vibrational patterns. Based on this, Scherk and Schwarz suggested that string theory had failed in its initial attempt because physicists had unduly constrained its scope. String theory is not just a theory of the strong force, they proclaimed; it is a quantum theory that includes gravity as well.3
The physics community did not receive this suggestion with unbridled enthusiasm. In fact, Schwarz recounts that "our work was universally ignored."4 The path of progress was already littered with numerous failed attempts to unite gravity and quantum mechanics. String theory had been shown wrong in its initial effort to describe the strong force, and it seemed to many that it was senseless to try to use the theory to pursue an even grander goal. Even more devastating, subsequent studies during the late 1970s and early 1980s showed that string theory and quantum mechanics suffered from their own subtle conflicts. It appeared that the gravitational force had, once again, resisted incorporation into the microscopic description of the universe.
Such was the case until 1984. In a landmark paper culminating more than a dozen years of intense research that had been largely ignored and often outright dismissed by most physicists, Green and Schwarz established that the subtle quantum conflict afflicting string theory could be resolved. Moreover, they showed that the resulting theory had sufficient breadth to encompass all of the four forces and all of matter as well. As word of this result spread throughout the worldwide physics community, particle physicists by the hundreds dropped their research projects to launch a full-scale assault on what appeared to be the last theoretical battleground in the ancient quest to understand the deepest workings of the universe.
I began graduate school at Oxford University in October 1984. Although I was excited to be learning about the likes of quantum field theory, gauge theory, and general relativity, there was a pervasive feeling among the older graduate students that there was little or no future for particle physics. The standard model was in place and its remarkable success at predicting experimental outcomes indicated that its verification was merely a matter of time and details. Going beyond its limits to include gravity and possibly to explain the experimental input on which it relies—the 19 numbers summarizing the elementary particle masses, their force charges, and the relative strengths of the forces, numbers that are known from experiment but are not understood theoretically—was so daunting a task that all but the most courageous physicists recoiled at the challenge. But six months later the mood had swung completely around. The success of Green and Schwarz finally trickled down even to first-year graduate students, and an electrifying sense of being on the inside of a profound moment in the history of physics displaced the previous ennui. A number of us consistently worked deep into the night to try to master the vast areas of theoretical physics and abstract mathematics that are required to understand string theory.
The period from 1984 to 1986 has come to be known as the "first superstring revolution." During those three years more than a thousand research papers on string theory were written by physicists from around the world. These works showed conclusively that numerous features of the standard model—features that had been painstakingly discovered over the course of decades of research—emerged naturally and simply from the grand structure of string theory. As Michael Green has said, "The moment you encounter string theory and realize that almost all of the major developments in physics over the last hundred years emerge—and emerge with such elegance—from such a simple starting point, you realize that this incredibly compelling theory is in a class of its own."5 Moreover, for many of these features, as we shall discuss, string theory offers a far fuller and more satisfying explanation than is found in the standard model. These developments convinced many physicists that string theory was well on its way to fulfilling its promise of being the ultimate unified theory.
Nonetheless, over and over again string theorists encountered a significant stumbling block. In theoretical physics research, one is frequently confronted with equations that are just too hard to understand or to analyze. Typically, physicists don't give up, but try to solve the equations approximately. The situation in string theory is even more difficult. Even determining the equations themselves has proved to be so difficult that only approximate versions of them have so far been deduced. String theorists have thereby been limited to finding approximate solutions to approximate equations. After the few years of dramatic progress during the first superstring revolution, physicists found that the approximations being used were inadequate to answer a number of essential questions hindering further developments. With no concrete proposals for going beyond the approximate methods, many physicists working on string theory grew frustrated and returned to their previous lines of research. For those who remained, the late 1980s and early 1990s were trying times. Like a golden treasure securely locked in a safe and visible only through a tiny, tantalizing peephole, the beauty and promise of string theory beckoned, but no one had the key to unlock its power. Long dry spells were periodically punctuated by important discoveries, but it was clear to everyone in the field that new methods with the power to go beyond the previous approximations were required.
Then, in a breathtaking lecture at the Strings 1995 conference held at the University of Southern California—a lecture that stunned a packed audience of the world's top physicists—Edward Witten announced a plan for taking the next step, thereby igniting the "second superstring revolution." String theorists, as of this writing, are working vigorously to sharpen a set of new methods that promise to overcome the theoretical obstacles previously encountered. The difficulties that lie ahead will severely test the technical might of the world's superstring theorists, but the light at the end of the tunnel, although still distant, may finally be becoming visible.
In this chapter and a number that follow, we shall describe the understanding of string theory that emerged from the first superstring revolution and subsequent work prior to the second superstring revolution. From time to time we will indicate new insights stemming from the latter; our discussion of these most recent advances will come in Chapters 12 and 13.
The Greeks' Atoms, Again?
As we mentioned at the outset of this chapter and as illustrated in Figure 1.1, string theory claims that if the presumed point-particles of the standard model could be examined with a precision significantly beyond our present capacity, each would be seen to be made of a single, tiny, oscillating loop of string.
For reasons that will become clear, the length of a typical string loop is about the Planck length, about a hundred billion billion (1020) times smaller than an atomic nucleus. It is no wonder that our present-day experiments are unable to resolve the microscopic stringy nature of matter: strings are minute even on the scales set by subatomic particles. We would need an accelerator to slam matter together with energies some million billion times more powerful than any previously constructed in order to reveal directly that a string is not a point-particle.
We will describe shortly the stunning implications that follow from replacing point-particles by strings, but let's first address a more basic question: What are strings made of?
There are two possible answers to this question. First, strings are truly fundamental—they are "atoms," uncuttable constituents, in the truest sense of the ancient Greeks. As the absolute smallest constituents of anything and everything, they represent the end of the line—the last of the Russian matrioshka dolls—in the numerous layers of substructure in the microscopic world. From this perspective, even though strings have spatial extent, the question of their composition is without any content. Were strings to be made of something smaller they would not be fundamental. Instead, whatever strings were composed of would immediately displace them and lay claim to being an even more basic constituent of the universe. Using our linguistic analogy, paragraphs are made of sentences, sentences are made of words, and words are made of letters. What makes up a letter? From a linguistic standpoint, that's the end of the line. Letters are letters—they are the fundamental building blocks of written language; there is no further substructure. Questioning their composition has no meaning. Similarly, a string is simply a string—as there is nothing more fundamental, it can't be described as being composed of any other substance.
That's the first answer. The second answer is based on the simple fact that as yet we do not know if string theory is a correct or final theory of nature. If string theory is truly off the mark, then, well, we can forget strings and the irrelevant question of their composition. Although this is a possibility, research since the mid-1980s overwhelmingly points toward its being extremely unlikely. But history surely has taught us that every time our understanding of the universe deepens, we find yet smaller microscopic ingredients constituting a finer level of matter. And so another possibility, should strings fail to be the final theory, is that they are one more layer in the cosmic onion, a layer that becomes visible at the Planck length, although not the final layer. In this case, strings could be made up of yet-smaller structures. String theorists have raised and continue to pursue this possibility. To date there are intriguing hints in theoretical studies that strings may have further substructure, but there is as yet no definitive evidence. Only time and intense research will supply the final word on this question.
Aside from a few speculations in Chapters 12 and 15, for our discussion here we approach strings in the manner proposed in the first answer—that is, we will take strings to be nature's most fundamental ingredient.
Unification through String Theory
Besides its inability to incorporate the gravitational force, the standard model has another shortcoming: There is no explanation for the details of its construction. Why did nature select the particular list of particles and forces outlined in previous chapters and recorded in Tables 1.1 and 1.2? Why do the 19 parameters that describe these ingredients quantitatively have the values that they do? You can't help feeling that their number and detailed properties seem so arbitrary. Is there a deeper understanding lurking behind these seemingly random ingredients, or were the detailed physical properties of the universe "chosen" by happenstance?
The standard model itself cannot possibly offer an explanation since it takes the list of particles and their properties as experimentally measured input. Just as the performance of the stock market cannot be used to determine the value of your portfolio without the input data of your initial investments, the standard model cannot be used to make any predictions without the input data of the fundamental particle properties.6 After experimental particle physicists fastidiously measure these data, theorists can then use the standard model to make testable predictions, such as what should happen when particular particles are slammed together in an accelerator. But the standard model can no more explain the fundamental particle properties of Tables 1.1 and 1.2 than the Dow Jones average today can explain your initial investment in stocks ten years ago.
In fact, had experiments revealed a somewhat different particle content in the microscopic world, possibly interacting with somewhat different forces, these changes could have been fairly easily incorporated in the standard model by providing the theory with different input parameters. The structure of the standard model, in this sense, is too flexible to be able to explain the properties of the elementary particles, as it could have accommodated a range of possibilities.
String theory is dramatically different. It is a unique and inflexible theoretical edifice. It requires no input beyond a single number, described below, that sets the benchmark scale for measurements. All properties of the microworld are within the realm of its explanatory power. To understand this, let's first think about more familiar strings, such as those on a violin. Each such string can undergo a huge variety (in fact, infinite in number) of different vibrational patterns known as resonances, such as those shown in Figure 6.1. These are the wave patterns whose peaks and troughs are evenly spaced and fit perfectly between the string's two fixed endpoints. Our ears sense these different resonant vibrational patterns as different musical notes. The strings in string theory have similar properties. There are resonant vibrational patterns that the string can support by virtue of their evenly spaced peaks and troughs exactly fitting along its spatial extent. Some examples are given in Figure 6.2. Here's the central fact: Just as the different vibrational patterns of a violin string give rise to different musical notes, the different vibrational patterns of a fundamental string give rise to different masses and force charges. As this is a crucial point, let's say it again. According to string theory, the properties of an elementary "particle"—its mass and its various force charges—are determined by the precise resonant pattern of vibration that its internal string executes.
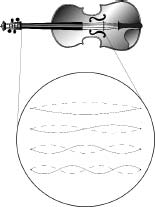
Figure 6.1 Strings on a violin can vibrate in resonant patterns in which a whole number of peaks and troughs exactly fit between the two ends.
It's easiest to understand this association for a particle's mass. The energy of a particular vibrational string pattern depends on its amplitude—the maximum displacement between peaks and troughs—and its wavelength—the separation between one peak and the next. The greater the amplitude and the shorter the wavelength, the greater the energy. This reflects what you would expect intuitively—more frantic vibrational patterns have more energy, while less frantic ones have less energy. We give a couple of examples in Figure 6.3. This is again familiar, as violin strings that are plucked more vigorously will vibrate more wildly, while those plucked more gingerly will vibrate more gently. Now, from special relativity we know that energy and mass are two sides of the same coin: Greater energy means greater mass, and vice versa. Thus, according to string theory, the mass of an elementary particle is determined by the energy of the vibrational pattern of its internal string. Heavier particles have internal strings that vibrate more energetically, while lighter particles have internal strings that vibrate less energetically.
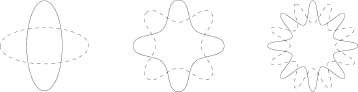
Figure 6.2 The loops in string theory can vibrate in resonance patterns—similar to those of violin strings—in which a whole number of peaks and troughs fit along their spatial extent.
Since the mass of a particle determines its gravitational properties, we see that there is a direct association between the pattern of string vibration and a particle's response to the gravitational force. Although the reasoning involved is somewhat more abstract, physicists have found that a similar alignment exists between other detailed aspects of a string's pattern of vibration and its properties vis a vis other forces. The electric charge, the weak charge, and the strong charge carried by a particular string, for instance, are determined by the precise way it vibrates. Moreover, exactly the same idea holds for the messenger particles themselves. Particles like photons, weak gauge bosons, and gluons are yet other resonant patterns of string vibration. And of particular importance, among the vibrational string patterns, one matches perfectly the properties of the graviton, ensuring that gravity is an integral part of string theory.7
So we see that, according to string theory, the observed properties of each elementary particle arise because its internal string undergoes a particular resonant vibrational pattern. This perspective differs sharply from that espoused by physicists before the discovery of string theory; in the earlier perspective the differences among the fundamental particles were explained by saying that, in effect, each particle species was "cut from a different fabric." Although each particle was viewed as elementary, the kind of "stuff" each embodied was thought to be different. Electron "stuff," for example, had negative electric charge, while neutrino "stuff" had no electric charge. String theory alters this picture radically by declaring that the "stuff" of all matter and all forces is the same. Each elementary particle is composed of a single string—that is, each particle is a single string—and all strings are absolutely identical. Differences between the particles arise because their respective strings undergo different resonant vibrational patterns. What appear to be different elementary particles are actually different "notes" on a fundamental string. The universe—being composed of an enormous number of these vibrating strings—is akin to a cosmic symphony.
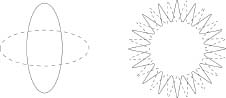
Figure 6.3 More frantic vibrational patterns have more energy than less frantic ones.
This overview shows how string theory offers a truly wonderful unifying framework. Every particle of matter and every transmitter of force consists of a string whose pattern of vibration is its "fingerprint." Because every physical event, process, or occurrence in the universe is, at its most elementary level, describable in terms of forces acting between these elementary material constituents, string theory provides the promise of a single, all-inclusive, unified description of the physical universe: a theory of everything (T.O.E.).
The Music of String Theory
Even though string theory does away with the previous concept of structureless elementary particles, old language dies hard, especially when it provides an accurate description of reality down to the most minute of distance scales. Following the common practice of the field we shall therefore continue to refer to "elementary particles," yet we will always mean "what appear to be elementary particles but are actually tiny pieces of vibrating string." In the preceding section we proposed that the masses and the force charges of such elementary particles are the result of the way in which their respective strings are vibrating. This leads us to the following realization: If we can work out precisely the allowed resonant vibrational patterns of fundamental strings—the "notes," so to speak, that they can play—we should be able to explain the observed properties of the elementary particles. For the first time, therefore, string theory sets up a framework for explaining the properties of the particles observed in nature.
At this stage, then, we should "grab hold" of a string and "pluck" it in all sorts of ways to determine the possible resonant patterns of vibration. If string theory is right, we should find that the possible patterns yield exactly the observed properties of the matter and force particles in Tables 1.1 and 1.2. Of course, a string is too small to carry out this experiment literally as described. Rather, by using mathematical descriptions we can theoretically pluck a string. In the mid-1980s, many string adherents believed that the mathematical analysis required for doing this was on the verge of being able to explain every detailed property of the universe on its most microscopic level. Some enthusiastic physicists declared that the T.O.E. had finally been discovered. More than a decade of hindsight has shown that the euphoria generated by this belief was premature. String theory has the makings of a T.O.E., but a number of hurdles remain, preventing us from deducing the spectrum of string vibrations with the precision necessary to compare with experimental results. At the present time, therefore, we do not know if the fundamental characteristics of our universe, summarized in Tables 1.1 and 1.2, can be explained by string theory. As we will discuss in Chapter 9, under certain assumptions that we will clearly state, string theory can give rise to a universe with properties that are in qualitative agreement with the known particle and force data, but extracting detailed numerical predictions from the theory is currently beyond our abilities. And so, although the framework of string theory, unlike that of the point-particle standard model, is capable of giving an explanation for why the particles and forces have the properties they do, we have not, as yet, been able to extract it. But remarkably, string theory is so rich and far-reaching that, even though we cannot yet determine its most detailed properties, we are able to gain insight into a wealth of the new physical phenomena that follow from the theory, as we will see in subsequent chapters.
In the following chapters we shall also discuss the status of the hurdles in some detail, but it is instructive first to understand them at a general level. Strings in the world around us come with a variety of tensions. The string laced through a pair of shoes, for example, is usually quite slack compared to the string stretched from one end of a violin to another. Both of these, in turn, are under far less tension than the steel strings of a piano. The one number that string theory requires in order to set its overall scale is the corresponding tension on its loops. How is this tension determined? Well, if we could pluck a fundamental string we would learn about its stiffness, and in this way we could measure its tension much as is done to measure the tension of more familiar everyday strings. But since fundamental strings are so tiny, this approach cannot be carried out and a more indirect method is called for. In 1974, when Scherk and Schwarz proposed that one particular pattern of string vibration was the graviton particle, they were able to exploit such an indirect approach and thereby predict the tension on the strings of string theory. Their calculations revealed that the strength of the force transmitted by the proposed graviton pattern of string vibration is inversely proportional to the string's tension. And since the graviton is supposed to transmit the gravitational force—a force that is intrinsically quite feeble—they found that this implies a colossal tension of a thousand billion billion billion billion (1039) tons, the so-called Planck tension. Fundamental strings are therefore extremely stiff compared with more familiar examples. This has three important consequences.
Three Consequences of Stiff Strings
First, whereas the ends of a violin or a piano string are pinned down, ensuring that they have a fixed length, no analogous constraining frame pins down the size of a fundamental string. Instead, the huge string tension causes the loops of string theory to contract to a minuscule size. Detailed calculation reveals that being under Planck tension translates into a typical string having Planck length—10-33 centimeters—as previously mentioned.8
Second, because of the enormous tension, the typical energy of a vibrating loop in string theory is extremely high. To understand this, we note that the greater the tension a string is under, the harder it is to get it to vibrate. For instance, it's far easier to pluck a violin string and set it vibrating than it is to pluck a piano string. Two strings, therefore, that are under different tension and are vibrating in precisely the same way will not have the same energy. The string with higher tension will have more energy than the string with lower tension, since more energy must be exerted to set it in motion.
This alerts us to the fact that the energy of a vibrating string is determined by two things: the precise manner in which it vibrates (more frantic patterns corresponding to higher energies) and the tension of the string (higher tension corresponding to higher energy). At first, this description might lead you to think that by taking on ever gentler vibrational patterns—patterns with ever smaller amplitudes and fewer peaks and troughs—a string can embody less and less energy. But as we found in Chapter 4 in a different context, quantum mechanics tells us that this reasoning is not right. Like all vibrations or wavelike disturbances, quantum mechanics implies that they can exist only in discrete units. Roughly speaking, just as the money carried by a comrade in the warehouse is a whole number multiple of the monetary denomination with which he or she is entrusted, the energy embodied in a string vibrational pattern is a whole number multiple of a minimal energy denomination. In particular, this minimal energy denomination is proportional to the tension of the string (and it is also proportional to the number of peaks and troughs in the particular vibrational pattern), while the whole number multiple is determined by the amplitude of the vibrational pattern.
The key point for the present discussion is this: Since the minimal energy denominations are proportional to the string's tension, and since this tension is enormous, the fundamental minimal energies are, on the usual scales of elementary particle physics, similarly huge. They are multiples of what is known as the Planck energy. To get a sense of scale, if we translate the Planck energy into a mass using Einstein's famous conversion formula E = mc2, they correspond to masses that are on the order of ten billion billion (1019) times that of a proton. This gargantuan mass—by elementary particle standards—is known as the Planck mass; it's about equal to the mass of a grain of dust or a collection of a million average bacteria. And so, the typical mass-equivalent of a vibrating loop in string theory is generally some whole number (1, 2, 3,…) times the Planck mass. Physicists often express this by saying that the "natural" or "typical" energy scale (and hence mass scale) of string theory is the Planck scale.
This raises a crucial question directly related to the goal of reproducing the particle properties in Tables 1.1 and 1.2: If the "natural" energy scale of string theory is some ten billion billion times that of a proton, how can it possibly account for the far-lighter particles—electrons, quarks, photons, and so on—making up the world around us?
The answer, once again, comes from quantum mechanics. The uncertainty principle ensures that nothing is ever perfectly at rest. All objects undergo quantum jitter, for if they didn't we would know where they were and how fast they were moving with complete precision, in violation of Heisenberg's dictum. This holds true for the loops in string theory as well; no matter how placid a string appears it will always experience some amount of quantum vibration. The remarkable thing, as originally worked out in the 1970s, is that there can be energy cancellations between these quantum jitters and the more intuitive kind of string vibrations discussed above and illustrated in Figures 6.2 and 6.3. In effect, through the weirdness of quantum mechanics, the energy associated with the quantum jitters of a string is negative, and this reduces the overall energy content of a vibrating string by an amount that is roughly equal to Planck energy. This means that the lowest-energy vibrational string patterns, whose energies we would naively expect to be about equal to the Planck energy(i.e., 1 times the Planck energy), are largely canceled, thereby yielding relatively low net-energy vibrations—energies whose corresponding mass-equivalents are in the neighborhood of the matter and force particle masses shown in Tables 1.1 and 1.2. It is these lowest energy vibrational patterns, therefore, that should provide contact between the theoretical description of strings and the experimentally accessible world of particle physics. As an important example, Scherk and Schwarz found that for the vibrational pattern whose properties make it a candidate for the graviton messenger particle, the energy cancellations are perfect, resulting in a zero-mass gravitational-force particle. This is precisely what is expected for the graviton; the gravitational force is transmitted at light speed and only massless particles travel at this maximal velocity. But low-energy vibrational combinations are very much the exception rather than the rule. The more typical vibrating fundamental string corresponds to a particle whose mass is billions upon billions times greater than that of the proton.
This tells us that the comparatively light fundamental particles of Tables 1.1 and 1.2 should arise, in a sense, from the fine mist above the roaring ocean of energetic strings. Even a particle as heavy as the top quark, with a mass about 189 times that of the proton, can arise from a vibrating string only if the string's enormous characteristic Planck-scale energy is canceled by the jitters of quantum uncertainty to better than one part in a hundred million billion. It's as if you were playing The Price Is Right and Bob Barker gives you ten billion billion dollars and challenges you to purchase products that will cost—cancel, so to speak—all but 189 of the dollars, not a dollar more or less. Coming up with such an enormous yet precise expenditure, without being privy to the exact prices of the individual items, would severely tax the acumen of even the world's most expert shoppers. In string theory, where the currency is energy as opposed to money, approximate calculations have conclusively shown that analogous energy cancellations certainly can occur, but for reasons that will become increasingly clear in subsequent chapters, verifying the cancellations to such a high level of precision is generally beyond our theoretical ken at present. Even so, as indicated before, we shall see that many other properties of string theory that are less sensitive to these finest of details can be extracted and understood with confidence.
This takes us to the third consequence of the enormous value of the string tension. Strings can execute an infinite number of different vibrational patterns. For instance, in Figure 6.2 we showed the beginnings of a never-ending sequence of possibilities characterized by an ever greater number of peaks and troughs. Doesn't this mean that there would have to be a corresponding never-ending sequence of elementary particles, seemingly in conflict with the experimental situation summarized in Tables 1.1 and 1.2?
The answer is yes: If string theory is right, each of the infinitely many resonant patterns of string vibration should correspond to an elementary particle. An essential point, however, is that the high string tension ensures that all but a few of these vibrational patterns will correspond to extremely heavy particles (the few being the lowest-energy vibrations that have near-perfect cancellations with quantum string jitters). And again, the term "heavy" here means many times heavier than the Planck mass. As our most powerful particle accelerators can reach energies only on the order of a thousand times the proton mass, less than a millionth of a billionth of the Planck energy, we are very far from being able to search in the laboratory for any of these new particles predicted by string theory.
There are more indirect approaches by which we could search for them, though. For instance, the energies involved at the birth of the universe would have been high enough to produce these particles copiously. In general one would not expect them to survive to the present day, as such super-heavy particles are usually unstable, relinquishing their enormous mass by decaying into a cascade of ever lighter particles, ending with the familiar, relatively light particles in the world around us. However, it is possible that such a super-heavy vibrational string state—a relic from the big bang—did survive to the present. Finding such particles, as we discuss more fully in Chapter 9, would be a monumental discovery, to say the least.
Gravity and Quantum Mechanics in String Theory
The unified framework that string theory presents is compelling. But its real attraction is the ability to ameliorate the hostilities between the gravitational force and quantum mechanics. Recall that the problem in merging general relativity and quantum mechanics turns up when the central tenet of the former—that space and time constitute a smoothly curving geometrical structure—confronts the essential feature of the latter—that everything in the universe, including the fabric of space and time, undergoes quantum fluctuations that become increasingly turbulent when probed on smaller and smaller distance scales. On sub-Planck-scale distances, the quantum undulations are so violent that they destroy the notion of a smoothly curving geometrical space; this means that general relativity breaks down.
String theory softens the violent quantum undulations by "smearing" out the short-distance properties of space. There is a rough and a more precise answer to the question of what this really means and how it resolves the conflict. We discuss each in turn.
The Rough Answer
Although it sounds unsophisticated, one way that we learn about the structure of an object is by hurling other things at it and observing the precise way in which they are deflected. We are able to see things, for example, because our eyes collect and our brains decode information carried by photons as they bounce off of objects being viewed. Particle accelerators are based on the same principle: They hurl bits of matter such as electrons and protons at each other as well as at other targets, and elaborate detectors analyze the resulting spray of debris to determine the architecture of the objects involved.
As a general rule, the size of the probe particle that we use sets a lower limit to the length scale to which we are sensitive. To get a feel for what this important statement means, imagine that Slim and Jim decide to get some culture by enrolling in a drawing class. As the semester progresses, Jim becomes increasingly irritated by Slim's growing proficiency as an artist and challenges him to an unusual contest. He proposes that they each take a peach pit, secure it in a vise, and draw their most accurate "still life" renditions. The unusual feature of Jim's challenge is that neither he nor Slim will be allowed to look at the peach pits. Instead, each is allowed to learn about the size, shape, and features of his peach pit only by shooting things (other than photons!) at the pit and observing how they are deflected, as illustrated in Figure 6.4. Unbeknownst to Slim, Jim fills Slim's "shooter" with marbles (as in Figure 6.4(a)) but fills his own shooter with far smaller five-millimeter plastic pellets (as in Figure 6.4(b)). They both turn on their shooters, and the competition begins.
After a while, the best drawing Slim can come up with is that in Figure 6.4(a). By observing the trajectories of the deflected marbles he was able to learn that the pit is a small, hard-surfaced mass. But that's all he could learn. Marbles are just too large to be sensitive to the finer corrugated structure of the peach pit. When Slim takes a look at Jim's drawing (Figure 6.4(b)), he is surprised to see that he has been outdone. A momentary glance at Jim's shooter, though, reveals the trick: The smaller probe particles used by Jim are fine enough to have their angle of deflection affected by some of the largest features adorning the pit's surface. And so, by shooting many five-millimeter pellets at the pit and observing their deflected trajectories, Jim was able to draw a more detailed image. Slim, not to be outdone, goes back to his shooter, fills it with even smaller probe particles—half-millimeter pellets—that are tiny enough to enter and hence be deflected by the finest corrugations on the pit's surface. By observing how these impinging probe particles are deflected, he is able to draw the winning rendition shown in Figure 6.4(c).
The lesson taught by this little competition is clear: Useful probe particles cannot be substantially larger than the physical features being examined; otherwise, they will be insensitive to the structures of interest.
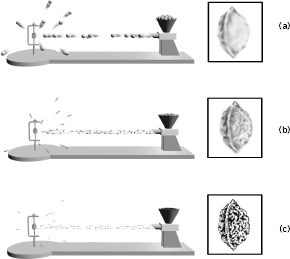
Figure 6.4 A peach pit is secured in a vise and it is drawn solely by observing how things—"probes"—thrown at it are deflected. By using ever smaller probes—(a) marbles, (b) five-millimeter pellets, (c) half-millimeter pellets—ever more detailed renditions can be drawn.
The same reasoning holds, of course, if one wants to probe the pit even more deeply to determine its atomic and subatomic structure. Half-millimeter pellets will not provide any useful information; they are clearly too big to have any sensitivity to structure on atomic scales. This is why particle accelerators use protons or electrons as probes, since their small size makes them much better suited to the task. On subatomic scales, where quantum concepts replace classical reasoning, the most appropriate measure of a particle's probing sensitivity is its quantum wavelength, which indicates the window of uncertainty in its position. This fact reflects our discussion of Heisenberg's uncertainty principle in Chapter 4, in which we found that the margin of error incurred when using a point particle as a probe (we focused on photon probes but the discussion applies to all other particles) is about equal to the probe particle's quantum wave-length. In somewhat looser language, the probing sensitivity of a point particle is smeared out by the jitteriness of quantum mechanics, in much the same way that the precision of a surgeon's scalpel is compromised if he or she has hands that shake. But recall that in Chapter 4 we also noted the important fact that a particle's quantum wavelength is inversely proportional to its momentum, which, roughly speaking, is its energy. And so, by increasing a point particle's energy, its quantum wavelength can be made shorter and shorter—quantum smearing can be decreased further and further—and hence we can use it to probe ever finer physical structures. Intuitively, higher-energy particles have greater penetrating power and are therefore able to probe more minute features.
In this regard, the distinction between point particles and strands of string becomes manifest. Just as was the case for plastic pellets probing the surface features of a peach pit, the string's inherent spatial extent prevents it from probing the structure of anything substantially smaller than its own size—in this case structures arising on length scales shorter than the Planck length. Somewhat more precisely, in 1988 David Gross, then of Princeton University, and his student Paul Mende showed that when quantum mechanics is taken into account, continually increasing the energy of a string does not continually increase its ability to probe finer structures, in direct contrast with what happens for a point particle. They found that when the energy of a string is increased, it is at first able to probe shorter-scale structures, just like an energetic point particle. But when its energy is increased beyond the value required for probing structures on the scale of the Planck length, the additional energy does not sharpen the string probe. Rather, the energy causes the string to grow in size, thereby diminishing its short-distance sensitivity. In fact, although the size of a typical string is the Planck length, if we pumped enough energy into a string—an amount of energy beyond our wildest imaginings but one that would likely have been attained by the big bang—we could cause it to grow to a macroscopic size, a clumsy probe of the microcosmos indeed! It's as if a string, unlike a point particle, has two sources of smearing: quantum jitters, as for a point particle, and also its own inherent spatial extent. Increasing a string's energy decreases the smearing from the first source but ultimately increases the smearing from the second. The upshot is that no matter how hard you try, the extended nature of a string prevents you from using it to probe phenomena on sub-Planck-length distances.
But the whole conflict between general relativity and quantum mechanics arises from the sub-Planck-length properties of the spatial fabric. If the elementary constituent of the universe cannot probe sub-Planck-scale distances, then neither it nor anything made from it can be affected by the supposedly disastrous short-distance quantum undulations. This is similar to what happens as we draw our hand across a highly polished granite surface. Although at a microscopic level the granite is discrete, grainy, and bumpy, our fingers are unable to detect these short-scale variations and the surface feels perfectly smooth. Our stumpy, extended fingers "smear" out the microscopic discreteness. Similarly, since the string has spatial extent, it also has limits on its short-distance sensitivity. It cannot detect variations on sub-Planck-distance scales. Like our fingers on granite, the string smears out the jittery ultramicroscopic fluctuations of the gravitational field. Although the resulting fluctuations are still substantial, this smearing smooths them out just enough to cure the incompatibility between general relativity and quantum mechanics. And, in particular, the pernicious infinities (discussed in the preceding chapter) that arise in the point-particle approach to forming a quantum theory of gravity are done away with by string theory.
An essential difference between the granite analogy and our real concern with the spatial fabric is that there are ways in which the microscopic discreteness of the granite's surface can be exposed: Finer, more precise probes than our fingers can be used. An electron microscope has the ability to resolve surface features to less than a millionth of a centimeter; this is sufficiently small to reveal the numerous surface imperfections. By contrast, in string theory there is no way to expose the sub-Planck-scale "imperfections" in the fabric of space. In a universe governed by the laws of string theory, the conventional notion that we can always dissect nature on ever smaller distances, without limit, is not true. There is a limit, and it comes into play before we encounter the devastating quantum foam of Figure 5.1. Therefore, in a sense that will be made more precise in later chapters, one can even say that the supposed tempestuous sub-Planckian quantum undulations do not exist. A positivist would say that something exists only if it can—at least in principle—be probed and measured. Since the string is supposed to be the most elementary object in the universe and since it is too large to be affected by the violent sub-Planck-length undulations of the spatial fabric, these fluctuations cannot be measured and hence, according to string theory, do not actually arise.
A Sleight of Hand?
This discussion may leave you feeling dissatisfied. Instead of showing that string theory tames the sub-Planck-length quantum undulations of space, we seem to have used the string's nonzero size to skirt the whole issue completely. Have we actually solved anything? We have. The following two points will serve to emphasize this.
First, what the preceding argument implies is that the supposedly problematic sub-Planck-length spatial fluctuations are an artifact of formulating general relativity and quantum mechanics in a point-particle framework. In a sense, therefore, the central conflict of contemporary theoretical physics has been a problem of our own making. Because we previously envisioned all matter particles and all force particles to be pointlike objects with literally no spatial extent, we were obligated to consider properties of the universe on arbitrarily short distance scales. And on the tiniest of distances we ran into seemingly insurmountable problems. String theory tells us that we encountered these problems only because we did not understand the true rules of the game; the new rules tell us that there is a limit to how finely we can probe the universe—and, in a real sense, a limit to how finely our conventional notion of distance can even be applied to the ultramicroscopic structure of the cosmos. The supposed pernicious spatial fluctuations are now seen to have arisen in our theories because we were unaware of these limits and were thus led by a point-particle approach to grossly overstep the bounds of physical reality.
Given the apparent simplicity of this solution for overcoming the problem between general relativity and quantum mechanics, you might wonder why it took so long for someone to suggest that the point-particle description is merely an idealization and that in the real world elementary particles do have some spatial extent. This takes us to our second point. Long ago, some of the greatest minds in theoretical physics, such as Pauli, Heisenberg, Dirac, and Feynman, did suggest that nature's constituents might not actually be points but rather small undulating "blobs" or "nuggets." They and others found, however, that it is very hard to construct a theory, whose fundamental constituent is not a point particle, that is nonetheless consistent with the most basic of physical principles such as conservation of quantum-mechanical probability (so that physical objects do not suddenly vanish from the universe, without a trace) and the impossibility of faster-than-light-speed transmission of information. From a variety of perspectives, their research showed time and again that one or both of these principles were violated when the point-particle paradigm was discarded. For a long time, therefore, it seemed impossible to find a sensible quantum theory based on anything but point particles. The truly impressive feature of string theory is that more than twenty years of exacting research has shown that although certain features are unfamiliar, string theory does respect all of the requisite properties inherent in any sensible physical theory. And furthermore, through its graviton pattern of vibration, string theory is a quantum theory containing gravity.
The More Precise Answer
The rough answer captures the essence of why string theory prevails where previous point-particle theories failed. And so, if you like, you can go on to the next section without losing the logical flow of our discussion. But having developed the essential ideas of special relativity in Chapter 2, we already have the necessary tools for describing more accurately how string theory calms the violent quantum jitters.
In the more precise answer, we rely upon the same core idea as in the rough answer, but we express it directly at the level of strings. We do this by comparing, in some detail, point-particle and string probes. We will see how the extended nature of the string smears out the information that would be obtainable by point-particle probes, and therefore, again, how it happily does away with the ultra-short-distance behavior responsible for the central dilemma of contemporary physics.
We first consider the way in which point particles would interact, if they were actually to exist, and hence how they could be used as physical probes. The most basic interaction is between two point particles moving on a collision course so that their trajectories will intersect, as in Figure 6.5. If these particles were billiard balls they would collide, and each would be deflected onto a new trajectory. Point-particle quantum field theory shows that essentially the same thing happens when elementary particles collide—they scatter off one another and continue on deflected trajectories—but the details are a little different.

Figure 6.5 Two particles interact—they "slam together"—and cause the path of each to be deflected.
For concreteness and simplicity, imagine that one of the two particles is an electron and the other is its antiparticle, the positron. When matter and antimatter collide, they can annihilate in a flash of pure energy, producing, for example, a photon.9 To distinguish the ensuing trajectory of the photon from the previous trajectories of the electron and positron, we follow a traditional physics convention and draw it with a wiggly line. The photon will typically travel for a bit and then release the energy derived from the initial electron-positron pair by producing another electron-positron pair with trajectories as indicated on the far right of Figure 6.6. In the end, two particles are fired at each other, they interact through the electromagnetic force, and finally they emerge on deflected trajectories, a sequence of events that bears some similarity to our description of colliding billiard balls.

Figure 6.6 In quantum field theory, a particle and its antiparticle can momentarily annihilate one another, producing a photon. Subsequently, this photon can give rise to another particle and antiparticle traveling along different trajectories.
We are concerned with the details of the interaction—specifically, the point where the initial electron and positron annihilate and produce the photon. The central fact, as will become apparent, is that there is an unambiguous, completely identifiable time and place where this happens: It is marked in Figure 6.6.
How does this description change if, when we closely examine the objects we thought were zero-dimensional points, they turn out to be one-dimensional strings? The basic process of interaction is the same, but now the objects on a collision course are oscillating loops, as shown in Figure 6.7. If these loops are vibrating in just the right resonance patterns, they will correspond to an electron and a positron on collision course, just as in Figure 6.6. Only when examined at the most minute distance scales, far smaller than anything our present technology can access, is their true stringlike character apparent. As in the point-particle case, the two strings collide and again annihilate each other in a flash. The flash, a photon, is itself a string in a particular vibrational pattern. Thus, the two incoming strings interact by merging together and producing a third string, as shown in Figure 6.7. Just as in our point-particle description, this string travels a bit, and then releases the energy derived from the two initial strings by dissociating into two strings that travel onward. Again, from any but the most microscopic perspective, this will look just like the point-particle interaction of Figure 6.6.
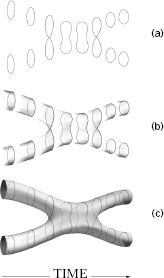
Figure 6.7 (a) Two strings on a collision course can merge into a third string, which subsequently can split apart into two strings travelling along deflected trajectories. (b) The same process as shown in (a), emphasizing string motion. (c) A "time-lapse photograph" of two interacting strings sweeping out a "world-sheet."
There is, however, a crucial difference between the two descriptions. We emphasized that the point-particle interaction occurs at an identifiable point in space and time, a location that all observers can agree on. As we shall now see, this is not true for interactions between strings. We will show this by comparing how George and Gracie, two observers in relative motion as in Chapter 2, would describe the interaction. We will see that they do not agree on where and when the two strings touch for the first time.
To do so, imagine that we view the interaction between two strings with a camera whose shutter is kept open so that the whole history of the process is captured on one piece of film.10 We show the result—known as a string world-sheet—in Figure 6.7(c). By "slicing" the world-sheet into parallel pieces—much as one slices a loaf of bread—the moment-by-moment history of the string interaction can be recovered. We show an example of this slicing in Figure 6.8. Specifically, in Figure 6.8(a) we show George, intently focused on the two incoming strings, together with an attached plane that slices through all events in space that occur at the same time, according to his perspective. As we have done often in previous chapters, we have suppressed one spatial dimension in this diagram for visual clarity. In reality, of course, there is a three-dimensional array of events that occur at the same time according to any observer. Figures 6.8(b) and 6.8(c) give a couple of snapshots at subsequent times—subsequent "slices" of the world-sheet—showing how George sees the two strings approach each other. Of central importance, in Figure 6.8(c) we show the instant in time, according to George, when the two strings first touch and merge together, producing the third string.
Let's now do the same for Gracie. As discussed in Chapter 2, the relative motion of George and Gracie implies that they do not agree on what events occur at the same time. From Gracie's perspective the events in space that occur simultaneously lie on a different plane, as shown in Figure 6.9. That is, from Gracie's perspective, the world-sheet of Figure 6.7(c) must be "sliced" into pieces at a different angle in order to reveal the moment-by-moment progression of the interaction.
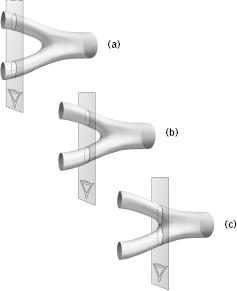
Figure 6.8 The two incoming strings from George's perspective at three consecutive moments in time. In (a) and (b) the strings are getting closer together; at (c) they touch for the first time, from his viewpoint.
In Figures 6.9(b) and 6.9(c) we show subsequent moments in time, now according to Gracie, including the moment when she sees the two incoming strings touch and produce the third string.
By comparing Figures 6.8(c) and 6.9(c), as we do in Figure 6.10, we see that George and Gracie do not agree on when and where the two initial strings first touch—where they interact. The string, being an extended object, ensures that there is no unambiguous location in space or moment in time when the strings first interact—rather, it depends upon the state of motion of the observer.
If we apply exactly the same reasoning to the interaction of point particles, as summarized in Figure 6.11, we recover the conclusion stated earlier—there is a definite point in space and moment in time when the point particles interact. Point particles cram all of their interaction into a definite point. When the force involved in an interaction is the gravitational force—that is, when the messenger particle involved in the interaction is the graviton instead of the photon—this complete packing of the force's punch into a single point leads to disastrous results, such as the infinite answers we alluded to earlier. Strings, by contrast, "smear" out the place where interactions occur. Because different observers perceive that the interaction takes place at various locations along the left part of the surface of Figure 6.10, in a real sense this means that the interaction location is smeared out among all of them. This spreads out the force's punch and, in the case of the gravitational force, this smearing significantly dilutes its ultramicroscopic properties—so much so that calculations yield well-behaved finite answers in place of the previous infinities. This is a more precise version of the smearing encountered in the rough answer of the last section. And once again, this smearing results in a smoothing of the ultramicroscopic jitteriness of space as sub-Planck-length distances are blurred together.
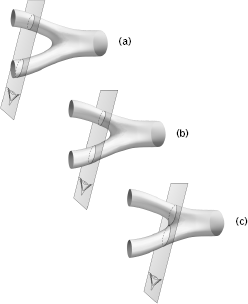
Figure 6.9 The two incoming strings from Gracie's perspective at three consecutive moments in time. In (a) and (b) the strings are getting closer together; at (c) they touch for the first time, from her viewpoint.

Figure 6.10 George and Gracie do not agree on the location of the interaction.
Like viewing the world through glasses that are too weak or too strong, fine sub-Planckian details that would be accessible to a point-particle probe are smeared together by string theory and rendered harmless. And unlike the case with poor eyesight, if string theory is the ultimate description of the universe, there is no corrective lens to bring the supposed sub-Planck-scale fluctuations into sharp focus. The incompatibility of general relativity and quantum mechanics—which would become apparent only on sub-Planck-scale distances—is avoided in a universe that has a lower limit on the distances that can be accessed, or even said to exist, in the conventional sense. Such is the universe described by string theory, in which we see that the laws of the large and the small can be harmoniously merged together as the supposed catastrophe arising on ultramicroscopic distances is summarily done away with.
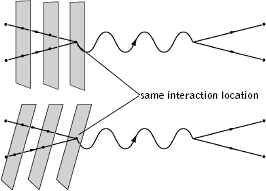
Figure 6.11 Observers in relative motion agree on when and where two point particles interact with another.
Beyond Strings?
Strings are special for two reasons. First, even though they are spatially extended they can be described consistently in the framework of quantum mechanics. Second, among the resonant vibrational patterns there is one that has the exact properties of the graviton, thus ensuring that the gravitational force is an intrinsic part of its structure. But just as string theory shows that the conventional notion of zero-dimensional point particles appears to be a mathematical idealization that is not realized in the real world, might it also be the case that an infinitely thin one-dimensional strand is similarly a mathematical idealization? Might it actually be the case that strings have some thickness—like the surface of a two-dimensional bicycle-tire inner tube or, even more realistically, like a thin three-dimensional doughnut? The seemingly insurmountable difficulties found by Heisenberg, Dirac, and others in their attempts to construct a quantum theory of three-dimensional nuggets have repeatedly stymied researchers following this natural chain of reasoning.
Quite unexpectedly, though, during the mid-1990s, string theorists realized, through indirect and rather shrewd reasoning, that such higher-dimensional fundamental objects actually do play an important and subtle role in string theory itself. Researchers have gradually realized that string theory is not a theory that contains only strings. A crucial observation, central to the second superstring revolution initiated by Witten and others in 1995, is that string theory actually includes ingredients with a variety of different dimensions: two-dimensional Frisbee-like constituents, three-dimensional blob-like constituents, and even more exotic possibilities to boot. These most recent realizations will be taken up in Chapters 12 and 13. For now we continue to follow the path of history and further explore the striking new properties of a universe built out of one-dimensional strings instead of zero-dimensional point-particles.