The Elegant Universe: Superstrings, Hidden Dimensions, and the Quest for the Ultimate Theory - Brian Greene (2010)
Part II. The Dilemma of Space, Time, and the Quanta
Chapter 4. Microscopic Weirdness
A bit worn out from their trans-solar-system expedition, George and Gracie return to earth and head over to the H-Bar for some post-space-sojourning refreshments. George orders the usual—papaya juice on the rocks for himself and a vodka tonic for Gracie—and kicks back in his chair, hands clasped behind his head, to enjoy a freshly lit cigar. Just as he prepares to inhale, though, he is stunned to find that the cigar has vanished from between his teeth. Thinking that the cigar must somehow have slipped from his mouth, George sits forward expecting to find it burning a hole in his shirt or trousers. But it is not there. The cigar is not to be found. Gracie, roused by George's frantic movement, glances over and spots the cigar lying on the counter directly behind George's chair. "Strange," George says, "how in the heck could it have fallen over there? It's as if it went right through my head—but my tongue isn't burned and I don't seem to have any new holes." Gracie examines George and reluctantly confirms that his tongue and head appear to be perfectly normal. As the drinks have just arrived, George and Gracie shrug their shoulders and chalk up the fallen cigar to one of life's little mysteries. But the weirdness at the H-Bar continues.
George looks into his papaya juice and notices that the ice cubes are incessantly rattling around—bouncing off of each other and the sides of the glass like overcharged automobiles in a bumper-car arena. And this time he is not alone. Gracie holds up her glass, which is about half the size of George's, and both of them see that her ice cubes are bouncing around even more frantically. They can hardly make out the individual cubes as they all blur together into an icy mass. But none of this compares to what happens next. As George and Gracie stare at her rattling drink with wide-eyed wonderment, they see a single ice cube pass through the side of her glass and drop down to the bar. They grab the glass and see that it is fully intact; somehow the ice cube went right through the solid glass without causing any damage. "Must be post-space-walk hallucinations," says George. They each fight off the frenzy of careening ice cubes to down their drinks in one go, and head home to recover. Little do George and Gracie realize that in their haste to leave, they mistook a decorative door painted on a wall of the bar for the real thing. The patrons of the H-Bar, though, are well accustomed to people passing through walls and hardly take note of George and Gracie's abrupt departure.
A century ago, while Conrad and Freud were illuminating the heart and the soul of darkness, the German physicist Max Planck shed the first ray of light on quantum mechanics, a conceptual framework that proclaims, among other things, that the H-Bar experiences of George and Gracie—when scaled down to the microscopic realm—need not be attributed to clouded faculties. Such unfamiliar and bizarre happenings are typical of how our universe, on extremely small scales, actually behaves.
The Quantum Framework
Quantum mechanics is a conceptual framework for understanding the microscopic properties of the universe. And just as special relativity and general relativity require dramatic changes in our worldview when things are moving very quickly or when they are very massive, quantum mechanics reveals that the universe has equally if not more startling properties when examined on atomic and subatomic distance scales. In 1965, Richard Feynman, one of the greatest practitioners of quantum mechanics, wrote,
There was a time when the newspapers said that only twelve men understood the theory of relativity. I do not believe there ever was such a time. There might have been a time when only one man did because he was the only guy who caught on, before he wrote his paper. But after people read the paper a lot of people understood the theory of relativity in one way or other, certainly more than twelve. On the other hand I think I can safely say that nobody understands quantum mechanics.1
Although Feynman expressed this view more than three decades ago, it applies equally well today. What he meant is that although the special and general theories of relativity require a drastic revision of previous ways of seeing the world, when one fully accepts the basic principles underlying them, the new and unfamiliar implications for space and time follow directly from careful logical reasoning. If you ponder the descriptions of Einstein's work in the preceding two chapters with adequate intensity, you will—if even for just a moment—recognize the inevitability of the conclusions we have drawn. Quantum mechanics is different. By 1928 or so, many of the mathematical formulas and rules of quantum mechanics had been put in place and, ever since, it has been used to make the most precise and successful numerical predictions in the history of science. But in a real sense those who use quantum mechanics find themselves following rules and formulas laid down by the "founding fathers" of the theory—calculational procedures that are straightforward to carry out—without really understanding why the procedures work or what they really mean. Unlike relativity, few if any people ever grasp quantum mechanics at a "soulful" level.
What are we to make of this? Does it mean that on a microscopic level the universe operates in ways so obscure and unfamiliar that the human mind, evolved over eons to cope with phenomena on familiar everyday scales, is unable to fully grasp "what really goes on"? Or, might it be that through historical accident physicists have constructed an extremely awkward formulation of quantum mechanics that, although quantitatively successful, obfuscates the true nature of reality? No one knows. Maybe some time in the future some clever person will see clear to a new formulation that will fully reveal the "whys" and the "whats" of quantum mechanics. And then again, maybe not. The only thing we know with certainty is that quantum mechanics absolutely and unequivocally shows us that a number of basic concepts essential to our understanding of the familiar everyday world fail to have any meaning when our focus narrows to the microscopic realm. As a result, we must significantly modify both our language and our reasoning when attempting to understand and explain the universe on atomic and subatomic scales.
In the following sections we will develop the basics of this language and describe a number of the remarkable surprises it entails. If along the way quantum mechanics seems to you to be altogether bizarre or even ludicrous, you should bear in mind two things. First, beyond the fact that it is a mathematically coherent theory, the only reason we believe in quantum mechanics is because it yields predictions that have been verified to astounding accuracy. If someone can tell you volumes of intimate details of your childhood in excruciating detail, it's hard not to believe their claim of being your long-lost sibling. Second, you are not alone in having this reaction to quantum mechanics. It is a view held to a greater or lesser extent by some of the most revered physicists of all time. Einstein refused to accept quantum mechanics fully. And even Niels Bohr, one of the central pioneers of quantum theory and one of its strongest proponents, once remarked that if you do not get dizzy sometimes when you think about quantum mechanics, then you have not really understood it.
It's Too Hot in the Kitchen
The road to quantum mechanics began with a puzzling problem. Imagine that your oven at home is perfectly insulated, that you set it to some temperature, say 400 degrees Fahrenheit, and you give it enough time to heat up. Even if you had sucked all the air from the oven before turning it on, by heating its walls you generate waves of radiation in its interior. This is the same kind of radiation—heat and light in the form of electromagnetic waves—that is emitted by the surface of the sun, or a glowing-hot iron poker.
Here's the problem. Electromagnetic waves carry energy—life on earth, for example, relies crucially on solar energy transmitted from the sun to the earth by electromagnetic waves. At the beginning of the twentieth century, physicists calculated the total energy carried by all of the electromagnetic radiation inside an oven at a chosen temperature. Using well-established calculational procedures they came up with a ridiculous answer: For any chosen temperature, the total energy in the oven is infinite.
It was clear to everyone that this was nonsense—a hot oven can embody significant energy but surely not an infinite amount. To understand the resolution proposed by Planck it is worth understanding the problem in a bit more detail. It turns out that when Maxwell's electromagnetic theory is applied to the radiation in an oven it shows that the waves generated by the hot walls must have a whole number of peaks and troughs that fit perfectly between opposite surfaces. Some examples are shown in Figure 4.1. Physicists use three terms to describe these waves: wavelength, frequency, and amplitude. The wavelengthis the distance between successive peaks or successive troughs of the waves, as illustrated in Figure 4.2. More peaks and troughs mean a shorter wavelength, as they must all be crammed in between the fixed walls of the oven. The frequency refers to the number of up-and-down cycles of oscillation that a wave completes every second. It turns out that the frequency is determined by the wavelength and vice versa: longer wavelengths imply lower frequency; shorter wavelengths imply higher frequency. To see why, think of what happens when you produce waves by shaking a long rope that is tied down at one end. To generate a long wavelength, you leisurely shake your end up and down. The frequency of the waves matches the number of cycles per second your arm goes through and is consequently fairly low. But to generate short wavelengths you shake your end more frantically—more frequently, so to speak—and this yields a higher-frequency wave. Finally, physicists use the term amplitude to describe the maximum height or depth of a wave, as also illustrated in Figure 4.2.
In case you find electromagnetic waves a bit abstract, another good analogy to keep in mind are the waves that are produced by plucking a violin string. Different wave frequencies correspond to different musical notes: the higher the frequency, the higher the note. The amplitude of a wave on a violin string is determined by how hard you pluck it. A harder pluck means that you put more energy into the wave disturbance; more energy therefore corresponds to a larger amplitude. You can hear this, as the resulting tone is louder. Similarly, less energy corresponds to a smaller amplitude and a lower volume of sound.

Figure 4.1 Maxwell's theory tells us that the radiation waves in an oven have a whole number of crests and troughs—they fill out complete wave-cycles.
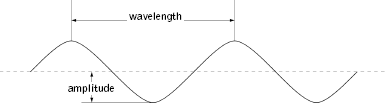
Figure 4.2 The wavelength is the distance between successive peaks or troughs of a wave. The amplitude is the maximal height or depth of the wave.
By making use of nineteenth-century thermodynamics, physicists were able to determine how much energy the hot walls of the oven would pump into electromagnetic waves of each allowed wavelength—how hard the walls would, in effect, "pluck" each wave. The result they found is simple to state: Each of the allowed waves—regardless of its wavelength—carries the same amount of energy (with the precise amount determined by the temperature of the oven). In other words, all of the possible wave patterns within the oven are on completely equal footing when it comes to the amount of energy they embody.
At first this seems like an interesting, albeit innocuous, result. It isn't. It spells the downfall of what has come to be known as classical physics. The reason is this: Even though requiring that all waves have a whole number of peaks and troughs rules out an enormous variety of conceivable wave patterns in the oven, there are still an infinite number that are possible—those with ever more peaks and troughs. Since each wave pattern carries the same amount of energy, an infinite number of them translates into an infinite amount of energy. At the turn of the century, there was a gargantuan fly in the theoretical ointment.
Making Lumps at the Turn of the Century
In 1900 Planck made an inspired guess that allowed a way out of this puzzle and would earn him the 1918 Nobel Prize in physics.2 To get a feel for his resolution, imagine that you and a huge crowd of people—"infinite" in number—are crammed into a large, cold warehouse run by a miserly landlord. There is a fancy digital thermostat on the wall that controls the temperature but you are shocked when you discover the charges that the landlord levies for heat. If the thermostat is set to 50 degrees Fahrenheit everyone must give the landlord $50. If it is set to 55 degrees everyone must pay $55, and so on. You realize that since you are sharing the warehouse with an infinite number of companions, the landlord will earn an infinite amount of money if you turn on the heat at all.
But on closer reading of the landlord's rules of payment you see a loophole. Because the landlord is a very busy man he does not want to give change, especially not to an infinite number of individual tenants. So he works on an honor system. Those who can pay exactly what they owe, do so. Otherwise, they pay only as much as they can without requiring change. And so, wanting to involve everyone but wanting to avoid the exorbitant charges for heat, you compel your comrades to organize the wealth of the group in the following manner: One person carries all of the pennies, one person carries all of the nickels, one carries all of the dimes, one carries all of the quarters, and so on through dollar bills, five-dollar bills, ten-dollar bills, twenties, fifties, hundreds, thousands, and ever larger (and unfamiliar) denominations. You brazenly set the thermostat to 80 degrees and await the landlord's arrival. When he does come, the person carrying pennies goes to pay first and turns over 8,000. The person carrying nickels then turns over 1,600 of them, the person carrying dimes turns over 800, the person with quarters turns over 320, the person with dollars gives the landlord 80, the person with five-dollar bills turns over 16, the person with ten-dollar bills gives him 8, the person with twenties gives him 4, and the person with fifties hands over one (since 2 fifty-dollar bills would exceed the necessary payment, thereby requiring change). But everyone else carries only a denomination—a minimal "lump" of money—that exceeds the required payment. Therefore they cannot pay the landlord and hence rather than getting the infinite amount of money he expected, the landlord leaves with the paltry sum of $690.
Planck made use of a very similar strategy to reduce the ridiculous result of infinite energy in an oven to one that is finite. Here's how. Planck boldly guessed that the energy carried by an electromagnetic wave in the oven, like money, comes in lumps. The energy can be one times some fundamental "energy denomination," or two times it, or three times it, and so forth—but that's it. Just as you can't have one-third of a penny or two and a half quarters, Planck declared that when it comes to energy, no fractions are allowed. Now, our monetary denominations are determined by the United States Treasury. Seeking a more fundamental explanation, Planck suggested that the energy denomination of a wave—the minimal lump of energy that it can have—is determined by its frequency. Specifically, he posited that the minimum energy a wave can have is proportional to its frequency: larger frequency (shorter wavelength) implies larger minimum energy; smaller frequency (longer wavelength) implies smaller minimum energy. Roughly speaking, just as gentle ocean waves are long and luxurious while harsh ones are short and choppy, long-wavelength radiation is intrinsically less energetic than short-wavelength radiation.
Here's the punch line: Planck's calculations showed that this lumpiness of the allowed energy in each wave cured the previous ridiculous result of infinite total energy. It's not hard to see why. When an oven is heated to some chosen temperature, the calculations based on nineteenth-century thermodynamics predicted the common energy that each and every wave would supposedly contribute to the total. But like those comrades who cannot contribute the common amount of money they each owe the landlord because the monetary denomination they carry is too large, if the minimum energy a particular wave can carry exceeds the energy it is supposed to contribute, it can't contribute and instead lies dormant. Since, according to Planck, the minimum energy a wave can carry is proportional to its frequency, as we examine waves in the oven of ever larger frequency (shorter wavelength), sooner or later the minimum energy they can carry is bigger than the expected energy contribution. Like the comrades in the warehouse entrusted with denominations larger than fifty-dollar bills, these waves with ever-larger frequencies cannot contribute the amount of energy demanded by nineteenth-century physics. And so, just as only a finite number of comrades are able to contribute to the total heat payment—leading to a finite amount of total money—only a finite number of waves are able to contribute to the oven's total energy—again leading to a finite amount of total energy. Be it energy or money, the lumpiness of the fundamental units—and the ever increasing size of these lumps as we go to higher frequencies or to larger monetary denominations—changes an infinite answer to one that is finite.3
By eliminating the manifest nonsense of an infinite result, Planck had taken an important step. But what really made people believe that his guess had validity is that the finite answer that his new approach gave for the energy in an oven agreed spectacularly with experimental measurements. Specifically, Planck found that by adjusting one parameter that entered into his new calculations, he could predict accurately the measured energy of an oven for any selected temperature. This one parameter is the proportionality factor between the frequency of a wave and the minimal lump of energy it can have. Planck found that this proportionality factor—now known as Planck's constant and denoted h (pronounced "h-bar")—is about a billionth of a billionth of a billionth in everyday units.4 The tiny value of Planck's constant means that the size of the energy lumps are typically very small. This is why, for example, it seems to us that we can cause the energy of a wave on a violin string—and hence the volume of sound it produces—to change continuously. In reality, though, the energy of the wave passes through discrete steps, a la Planck, but the size of the steps is so small that the discrete jumps from one volume to another appear to be smooth. According to Planck's assertion, the size of these jumps in energy grows as the frequency of the waves gets higher and higher (while wavelengths get shorter and shorter). This is the crucial ingredient that resolves the infinite-energy paradox.
As we shall see, Planck's quantum hypothesis does far more than allow us to understand the energy content of an oven. It overturns much about the world that we hold to be self-evident. The smallness of h confines most of these radical departures from life-as-usual to the microscopic realm, but if h happened to be much larger than it is, the strange happenings at the H-Bar would actually be commonplace. As we shall see, their microscopic counterparts certainly are.
What Are the Lumps?
Planck had no justification for his pivotal introduction of lumpy energy. Beyond the fact that it worked, neither he nor anyone else could give a compelling reason for why it should be true. As the physicist George Gamow once said, it was as if nature allowed one to drink a whole pint of beer or no beer at all, but nothing in between.5 In 1905, Einstein found an explanation and for this insight he was awarded the 1921 Nobel Prize in physics.
Einstein came up with his explanation by puzzling over something known as the photoelectric effect. The German physicist Heinrich Hertz in 1887 was the first to find that when electromagnetic radiation—light—shines on certain metals, they emit electrons. By itself this is not particularly remarkable. Metals have the property that some of their electrons are only loosely bound within atoms (which is why they are such good conductors of electricity). When light strikes the metallic surface it relinquishes its energy, much as it does when it strikes the surface of your skin, causing you to feel warmer. This transfered energy can agitate electrons in the metal, and some of the loosely bound ones can be knocked clear off the surface.
But the strange features of the photoelectric effect become apparent when one studies more detailed properties of the ejected electrons. At first sight you would think that as the intensity of the light—its brightness—is increased, the speed of the ejected electrons will also increase, since the impinging electromagnetic wave has more energy. But this does not happen. Rather, the number of ejected electrons increases, but their speed stays fixed. On the other hand, it has been experimentally observed that the speed of the ejected electrons does increase if the frequency of the impinging light is increased, and, equivalently, their speed decreases if the frequency of the light is decreased. (For electromagnetic waves in the visible part of the spectrum, an increase in frequency corresponds to a change in color from red to orange to yellow to green to blue to indigo and finally to violet. Frequencies higher than that of violet are not visible and correspond to ultraviolet and, subsequently, X rays; frequencies lower than that of red are also not visible, and correspond to infrared radiation.) In fact, as the frequency of the light used is decreased, there comes a point when the speed of the emitted electrons drops to zero and they stop being ejected from the surface, regardless of the possibly blinding intensity of the light source. For some unknown reason, the color of the impinging light beam—not its total energy—controls whether or not electrons are ejected, and if they are, the energy they have.
To understand how Einstein explained these puzzling facts, let's go back to the warehouse, which has now heated up to a balmy 80 degrees. Imagine that the landlord, who hates children, requires everyone under the age of fifteen to live in the sunken basement of the warehouse, which the adults can view from a huge wraparound balcony. Moreover, the only way any of the enormous number of basement-bound children can leave the warehouse is if they can pay the guard an 85-cent exit fee. (This landlord is such an ogre.) The adults, who at your urging have arranged the collective wealth by denomination as described above, can give money to the children only by throwing it down to them from the balcony. Let's see what happens.
The person carrying pennies begins by tossing a few down, but this is far too meagre a sum for any of the children to be able to afford the departure fee. And because there is an essentially "infinite" sea of children all ferociously fighting in a turbulent tumult for the falling money, even if the penny-entrusted adult throws enormous numbers down, no individual child will come anywhere near collecting the 85 he or she needs to pay the guard. The same is true for the adults carrying nickels, dimes, and quarters. Although each tosses down a staggeringly large total amount of money, any single child is lucky if he or she gets even one coin (most get nothing at all) and certainly no child collects the 85 cents necessary to leave. But then, when the adult carrying dollars starts throwing them down—even comparatively tiny sums, dollar by single dollar—those lucky children who catch a single bill are able to leave immediately. Notice, though, that even as this adult loosens up and throws down barrels of dollar bills, the number of children who are able to leave increases enormously, but each has exactly 15 cents left after paying the guard. This is true regardless of the total number of dollars tossed.
Here is what all this has to do with the photoelectric effect. Based on the experimental data reviewed above, Einstein suggested incorporating Planck's lumpy picture of wave energy into a new description of light. A light beam, according to Einstein, should actually be thought of as a stream of tiny packets—tiny particles of light—which were ultimately christened photons by the chemist Gilbert Lewis (an idea we made use of in our example of the light clock of Chapter 2). To get a sense of scale, according to this particle view of light, a typical one-hundred-watt bulb emits about a hundred billion billion (1020) photons per second. Einstein used this new conception to suggest a microscopic mechanism underlying the photoelectric effect: An electron is knocked off a metallic surface, he proposed, if it gets hit by a sufficiently energetic photon. And what determines the energy of an individual photon? To explain the experimental data, Einstein followed Planck's lead and proposed that the energy of each photon is proportional to the frequency of the light wave (with the proportionality factor being Planck's constant).
Now, like the children's minimum departure fee, the electrons in a metal must be jostled by a photon posessing a certain minimum energy in order to be kicked off the surface. (As with the children fighting for money, it is extremely unlikely that any one electron gets hit by more than one photon—most don't get hit at all.) But if the impinging light beam's frequency is too low, its individual photons will lack the punch necessary to eject electrons. Just as no children can afford to leave regardless of the huge total number of coins the adults shower upon them, no electrons are jostled free regardless of the huge total energy embodied in the impinging light beam, if its frequency (and thus the energy of its individual photons) is too low.
But just as children are able to leave the warehouse as soon as the monetary denomination showered upon them gets large enough, electrons will be knocked off the surface as soon as the frequency of the light shone on them—its energy denomination—gets high enough. Moreover, just as the dollar-entrusted adult increases the total money thrown down by increasing the number of individual bills tossed, the total intensity of a light beam of a chosen frequency is increased by increasing the number of photons it contains. And just as more dollars result in more children being able to leave, more photons result in more electrons being hit and knocked clear off the surface. But notice that the leftover energy that each of these electrons has after ripping free of the surface depends solely on the energy of the photon that hits it—and this is determined by the frequency of the light beam, not its total intensity. Just as children leave the basement with 15 cents no matter how many dollar bills are thrown down, each electron leaves the surface with the same energy—and hence the same speed—regardless of the total intensity of the impinging light. More total money simply means more children can leave; more total energy in the light beam simply means more electrons are knocked free. If we want children to leave the basement with more money, we must increase the monetary denomination tossed down; if we want electrons to leave the surface with greater speed, we must increase the frequency of the impinging light beam—that is, we must increase the energy denomination of the photons we shine on the metallic surface.
This is precisely in accord with the experimental data. The frequency of the light (its color) determines the speed of the ejected electrons; the total intensity of the light determines the number of ejected electrons. And so Einstein showed that Planck's guess of lumpy energy actually reflects a fundamental feature of electromagnetic waves: They are composed of particles—photons—that are little bundles, or quanta, of light. The lumpiness of the energy embodied by such waves is due to their being composed of lumps.
Einstein's insight represented great progress. But, as we shall now see, the story is not as tidy as it might appear.
Is It a Wave or Is It a Particle?
Everyone knows that water—and hence water waves—are composed of a huge number of water molecules. So is it really surprising that light waves are also composed of a huge number of particles, namely photons? It is. But the surprise is in the details. You see, more than three hundred years ago Newton proclaimed that light consisted of a stream of particles, so the idea is not exactly new. However, some of Newton's colleagues, most notably the Dutch physicist Christian Huygens, disagreed with him and argued that light is a wave. The debate raged but ultimately experiments carried out by the English physicist Thomas Young in the early 1800s showed that Newton was wrong.
A version of Young's experimental setup—known as the double-slit experiment—is schematically illustrated in Figure 4.3. Feynman was fond of saying that all of quantum mechanics can be gleaned from carefully thinking through the implications of this single experiment, so it's well worth discussing. As we see from Figure 4.3, light is shone on a thin solid barrier in which two slits are cut. A photographic plate records the light that gets through the slits—brighter areas of the photograph indicate more incident light. The experiment consists of comparing the images on photographic plates that result when either or both of the slits in the barrier are kept open and the light source is turned on.
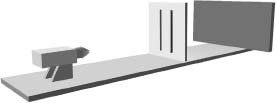
Figure 4.3 In the double-slit experiment, a beam of light is shone on a barrier in which two slits have been cut. The light that passes through the barrier is then recorded on a photographic plate, when either or both of the slits are open.
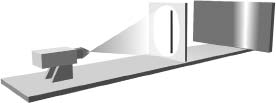
Figure 4.4 The right slit is open in this experiment, leading to an image on the photographic plate as shown.
If the left slit is covered and the right slit is open, the photograph looks like that shown in Figure 4.4. This makes good sense, since the light that hits the photographic plate must pass through the only open slit and will therefore be concentrated around the right part of the photograph. Similarly, if the right slit is covered and the left slit open, the photograph will look like that in Figure 4.5. If both slits are open, Newton's particle picture of light leads to the prediction that the photographic plate will look like that in Figure 4.6, an amalgam of Figures 4.4 and 4.5. In essence, if you think of Newton's corpuscles of light as if they were little pellets you fire at the wall, the ones that get through will be concentrated in the two areas that line up with the two slits. The wave picture of light, on the contrary, leads to a very different prediction for what happens when both slits are open. Let's see this.
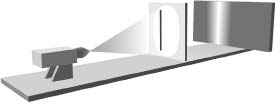
Figure 4.5 As in Figure 4.4, except now only the left slit is open.
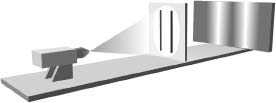
Figure 4.6 Newton's particle view of light predicts that when both slits are open, the photographic plate will be a merger of the images in Figures 4.4 and 4.5.
Imagine for a moment that rather than dealing with light waves we use water waves. The result we will find is the same, but water is easier to think about. When water waves strike the barrier, outgoing circular water waves emerge from each slit, much like those created by throwing a pebble into a pond, as illustrated in Figure 4.7. (It is simple to try this using a cardboard barrier with two slits in a pan of water.) As the waves emerging from each slit overlap with each other, something quite interesting happens. If two wave peaks overlap, the height of the water wave at that point increases: It's the sum of the heights of the two individual peaks. If two wave troughs overlap, the depth of the water depression at that point is similarly increased. And finally, if a wave peak emerging from one slit overlaps with a wave trough emerging from the other, they cancel each other out. (In fact, this is the idea behind fancy noise-eliminating head-phones—they measure the shape of the incoming sound wave and then produce another whose shape is exactly "opposite," leading to a cancellation of the undesired noise.) In between these extreme overlaps—peaks with peaks, troughs with troughs, and peaks with troughs—are a host of partial height augmentations and cancellations. If you and a slew of companions form a line of little boats parallel to the barrier and you each declare how severely you are jostled by the resulting water wave as it passes, the result will look something like that shown on the far right of Figure 4.7. Locations of significant jostling are where wave peaks (or troughs) from each slit coincide. Regions of minimal or no jostling are where peaks from one slit coincide with troughs from the other, resulting in a cancellation.

Figure 4.7 Circular water waves that emerge from each slit overlap with each other, causing the total wave to be increased at some locations and decreased at others.
Since the photographic plate records how much it is "jostled" by the incoming light, exactly the same reasoning applied to the wave picture of a light beam tells us that when both slits are open the photograph will look like that in Figure 4.8. The brightest areas in Figure 4.8 are where light-wave peaks (or troughs) from each slit coincide. Dark areas are where wave peaks from one slit coincide with wave troughs from the other, resulting in a cancellation. The sequence of light and dark bands is known as an interference pattern. This photograph is significantly different from that shown in Figure 4.6, and hence there is a concrete experiment to distinguish between the particle and the wave pictures of light. Young carried out a version of this experiment and his results matched Figure 4.8, thereby confirming the wave picture. Newton's corpuscular view was defeated (although it took quite some time before physicists accepted this). The prevailing wave view of light was subsequently put on a mathematically firm foundation by Maxwell.
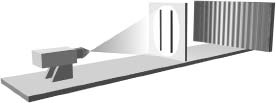
Figure 4.8 If light is a wave, then when both slits are open there will be interference between the portions of the wave emerging from each slit.
But Einstein, the man who brought down Newton's revered theory of gravity, seems now to have resurrected Newton's particle model of light by his introduction of photons. Of course, we still face the same question: How can a particle perspective account for the interference pattern shown in Figure 4.8? At first blush you might make the following suggestion. Water is composed of H2O molecules—the "particles" of water. Nevertheless, when a lot of these molecules stream along with one another they can produce water waves, with the attendant interference properties illustrated in Figure 4.7. And so, it might seem reasonable to guess that wave properties, such as interference patterns, can arise from a particle picture of light provided a huge number of photons, the particles of light, are involved.
In reality, though, the microscopic world is far more subtle. Even if the intensity of the light source in Figure 4.8 is turned down and down, finally to the point where individual photons are being fired one by one at the barrier—say at the rate of one every ten seconds—the resulting photographic plate will still look like that in Figure 4.8: So long as we wait long enough for a huge number of these separate bundles of light to make it through the slits and to each be recorded by a single dot where they hit the photographic plate, these dots will build up to form the image of an interference pattern, the image in Figure 4.8. This is astounding. How can individual photon particles that sequentially pass through the screen and separately hit the photographic plate conspire to produce the bright and dark bands of interfering waves? Conventional reasoning tells us that each and every photon passes through either the left slit or the right slit and we would therefore expect to find the pattern shown in Figure 4.6. But we don't.
If you are not bowled over by this fact of nature, it means that either you have seen it before and have become blase or the description so far has not been sufficiently vivid. So, in case it's the latter, let's describe it again, but in a slightly different way. You close off the left slit and fire the photons one by one at the barrier. Some get through, some don't. The ones that do create an image on the photographic plate, dot by single dot, which looks like that in Figure 4.4. You then run the experiment again with a new photographic plate, but this time you open both slits. Naturally enough, you think that this will only increase the number of photons that pass through the slits in the barrier and hit the photographic plate, thereby exposing the film to more total light than in your first run of the experiment. But when you later examine the image produced, you find that not only are there places on the photographic plate that were dark in the first experiment and are now bright, as expected, there are also places on the photographic plate that were bright in your first experiment but are now dark, as in Figure 4.8. By increasing the number of individual photons that hit the photographic plate you have decreased the brightness in certain areas. Somehow, temporally separated, individual particulate photons are able to cancel each other out. Think about how crazy this is: Photons that would have passed through the right slit and hit the film in one of the dark bands in Figure 4.8 fail to do so when the left slit is opened (which is why the band is now dark). But how in the world can a tiny bundle of light that passes through one slit be at all affected by whether or not the otherslit is open? As Feynman noted, it's as strange as if you fire a machine gun at the screen, and when both slits are open, independent, separately fired bullets somehow cancel one another out, leaving a pattern of unscathed positions on the target—positions that are hit when only one slit in the barrier is open.
Such experiments show that Einstein's particles of light are quite different from Newton's. Somehow photons—although they are particles—embody wave-like features of light as well. The fact that the energy of these particles is determined by a wave-like feature—frequency—is the first clue that a strange union is occurring. But the photoelectric effect and the double-slit experiment really bring the lesson home. The photoelectric effect shows that light has particle properties. The double-slit experiment shows that light manifests the interference properties of waves. Together they show that light has both wave-like and particle-like properties. The microscopic world demands that we shed our intuition that something is either a wave or a particle and embrace the possibility that it is both. It is here that Feynman's pronouncement that "nobody understands quantum mechanics" comes to the fore. We can utter words such as "wave-particle duality." We can translate these words into a mathematical formalism that describes real-world experiments with amazing accuracy. But it is extremely hard to understand at a deep, intuitive level this dazzling feature of the microscopic world.
Matter Particles Are Also Waves
In the first few decades of the twentieth century, many of the greatest theoretical physicists grappled tirelessly to develop a mathematically sound and physically sensible understanding of these hitherto hidden microscopic features of reality. Under the leadership of Niels Bohr in Copenhagen, for example, substantial progress was made in explaining the properties of light emitted by glowing-hot hydrogen atoms. But this and other work prior to the mid-1920s was more a makeshift union of nineteenth-century ideas with newfound quantum concepts than a coherent framework for understanding the physical universe. Compared with the clear, logical framework of Newton's laws of motion or Maxwell's electromagnetic theory, the partially developed quantum theory was in a chaotic state.
In 1923, the young French nobleman Prince Louis de Broglie added a new element to the quantum fray, one that would shortly help to usher in the mathematical framework of modern quantum mechanics and that earned him the 1929 Nobel Prize in physics. Inspired by a chain of reasoning rooted in Einstein's special relativity, de Broglie suggested that the wave-particle duality applied not only to light but to matter as well. He reasoned, roughly speaking, that Einstein's E = mc2 relates mass to energy, that Planck and Einstein had related energy to the frequency of waves, and therefore, by combining the two, mass should have a wave-like incarnation as well. After carefully working through this line of thought, he suggested that just as light is a wave phenomenon that quantum theory shows to have an equally valid particle description, an electron—which we normally think of as being a particle—might have an equally valid description in terms of waves. Einstein immediately took to de Broglie's idea, as it was a natural outgrowth of his own contributions of relativity and of photons. Even so, nothing is a substitute for experimental proof. Such proof was soon to come from the work of Clinton Davisson and Lester Germer.
In the mid-1920s, Davisson and Germer, experimental physicists at the Bell telephone company, were studying how a beam of electrons bounces off of a chunk of nickel. The only detail that matters for us is that the nickel crystals in such an experiment act very much like the two slits in the experiment illustrated by the figures of the last section—in fact, it's perfectly okay to think of this experiment as being the same one illustrated there, except that a beam of electrons is used in place of a beam of light. We will adopt this point of view. When Davisson and Germer examined electrons making it through the two slits in the barrier by allowing them to hit a phosphorescent screen that recorded the location of impact of each electron by a bright dot—essentially what happens inside a television—they found something remarkable. A pattern very much akin to that of Figure 4.8 emerged. Their experiment therefore showed that electrons exhibit interference phenomena, the telltale sign of waves. At dark spots on the phosphorescent screen, electrons were somehow "canceling each other out" just like the overlapping peak and trough of water waves. Even if the beam of fired electrons was "thinned" so that, for instance, only one electron was emitted every ten seconds, the individual electrons still built up the bright and dark bands—one spot at a time. Somehow, as with photons, individual electrons "interfere" with themselves in the sense that individual electrons, over time, reconstruct the interference pattern associated with waves. We are inescapably forced to conclude that each electron embodies a wave-like character in conjunction with its more familiar depiction as a particle.
Although we have described this in the case of electrons, similar experiments lead to the conclusion that all matter has a wave-like character. But how does this jibe with our real-world experience of matter as being solid and sturdy, and in no way wave-like? Well, de Broglie set down a formula for the wavelength of matter waves, and it shows that the wavelength is proportional to Planck's constant h. (More precisely, the wavelength is given by h divided by the material body's momentum.) Since h is so small, the resulting wavelengths are similarly minuscule compared with everyday scales. This is why the wave-like character of matter becomes directly apparent only upon careful microscopic investigation. Just as the large value of c, the speed of light, obscures much of the true nature of space and time, the smallness of hobscures the wave-like aspects of matter in the day-to-day world.
Waves of What?
The interference phenomenon found by Davisson and Germer made the wave-like nature of electrons tangibly evident. But waves of what? One early suggestion made by Austrian physicist Erwin Schrödinger was that the waves were "smeared-out" electrons. This captured some of the "feeling" of an electron wave, but it was too rough. When you smear something out, part of it is here and part of it is there. However, one never encounters half of an electron or a third of an electron or any other fraction, for that matter. This makes it hard to grasp what a smeared electron actually is. As an alternative, in 1926 German physicist Max Born sharply refined Schrödinger's interpretation of an electron wave, and it is his interpretation—amplified by Bohr and his colleagues—that is still with us today. Born's suggestion is one of the strangest features of quantum theory, but is supported nonetheless by an enormous amount of experimental data. He asserted that an electron wave must be interpreted from the standpoint of probability. Places where the magnitude (a bit more correctly, the square of magnitude) of the wave is large are places where the electron is more likely to be found; places where the magnitude is small are places where the electron is less likely to be found. An example is illustrated in Figure 4.9.
This is truly a peculiar idea. What business does probability have in the formulation of fundamental physics? We are accustomed to probability showing up in horse races, in coin tosses, and at the roulette table, but in those cases it merely reflects our incomplete knowledge. If we knew precisely the speed of the roulette wheel, the weight and hardness of the white marble, the location and speed of the marble when it drops to the wheel, the exact specifications of the material constituting the cubicles and so on, and if we made use of sufficiently powerful computers to carry out our calculations we would, according to classical physics, be able to predict with certainty where the marble would settle. Gambling casinos rely on your inability to ascertain all of this information and to do the necessary calculations prior to placing your bet. But we see that probability as encountered at the roulette table does not reflect anything particularly fundamental about how the world works. Quantum mechanics, on the contrary, injects the concept of probability into the universe at a far deeper level. According to Born and more than half a century of subsequent experiments, the wave nature of matter implies that matter itself must be described fundamentally in a probabilistic manner. For macroscopic objects like a coffee cup or the roulette wheel, de Broglie's rule shows that the wave-like character is virtually unnoticeable and for most ordinary purposes the associated quantum-mechanical probability can be completely ignored. But at a microscopic level we learn that the best we can ever do is say that an electron has a particular probability of being found at any given location.
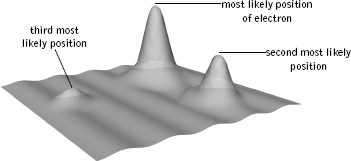
Figure 4.9 The wave associated with an electron is largest where the electron is most likely to be found, and progressively smaller at locations where it is less likely to be found.
The probabilistic interpretation has the virtue that if an electron wave does what other waves can do—for instance, slam into some obstacle and develop all sorts of distinct ripples—it does not mean that the electron itself has shattered into separate pieces. Rather, it means that there are now a number of locations where the electron might be found with a nonnegligible probability. In practice this means that if a particular experiment involving an electron is repeated over and over again in an absolutely identical manner, the same answer for, say, the measured position of an electron will not be found over and over again. Rather, the subsequent repeats of the experiment will yield a variety of different results with the property that the number of times the electron is found at any given location is governed by the shape of the electron's probability wave. If the probability wave (more precisely, the square of the probability wave) is twice as large at location A than at location B, then the theory predicts that in a sequence of many repeats of the experiment the electron will be found at location A twice as often as at location B. Exact outcomes of experiments cannot be predicted; the best we can do is predict the probability that any given outcome may occur.
Even so, as long as we can determine mathematically the precise form of probability waves, their probabilistic predictions can be tested by repeating a given experiment numerous times, thereby experimentally measuring the likelihood of getting one particular result or another. Just a few months after de Broglie's suggestion, Schrödinger took the decisive step toward this end by determining an equation that governs the shape and the evolution of probability waves, or as they came to be known, wave functions. It was not long before Schrödinger's equation and the probabilistic interpretation were being used to make wonderfully accurate predictions. By 1927, therefore, classical innocence had been lost. Gone were the days of a clockwork universe whose individual constituents were set in motion at some moment in the past and obediently fulfilled their inescapable, uniquely determined destiny. According to quantum mechanics, the universe evolves according to a rigorous and precise mathematical formalism, but this framework determines only the probability that any particular future will happen—not which future actually ensues.
Many find this conclusion troubling or even downright unacceptable. Einstein was one. In one of physics' most time-honored utterances, Einstein admonished the quantum stalwarts that "God does not play dice with the Universe." He felt that probability was turning up in fundamental physics because of a subtle version of the reason it turns up at the roulette wheel: some basic incompleteness in our understanding. The universe, in Einstein's view, had no room for a future whose precise form involves an element of chance. Physics should predict how the universe evolves, not merely the likelihood that any particular evolution might occur. But experiment after experiment—some of the most convincing ones being carried out after his death—convincingly confirm that Einstein was wrong. As the British theoretical physicist Stephen Hawking has said, on this point "Einstein was confused, not the quantum theory."6
Nevertheless, the debate about what quantum mechanics really means continues unabated. Everyone agrees on how to use the equations of quantum theory to make accurate predictions. But there is no consensus on what it really means to have probability waves, nor on how a particle "chooses" which of its many possible futures to follow, nor even on whether it really does choose or instead splits off like a branching tributary to live out all possible futures in an ever-expanding arena of parallel universes. These interpretational issues are worthy of a book-length discussion in their own right, and, in fact, there are many excellent books that espouse one or another way of thinking about quantum theory. But what appears certain is that no matter how you interpret quantum mechanics, it undeniably shows that the universe is founded on principles that, from the standpoint of our day-to-day experiences, are bizarre.
The meta-lesson of both relativity and quantum mechanics is that when we deeply probe the fundamental workings of the universe we may come upon aspects that are vastly different from our expectations. The boldness of asking deep questions may require unforeseen flexibility if we are to accept the answers.
Feynman's Perspective
Richard Feynman was one of the greatest theoretical physicists since Einstein. He fully accepted the probabilistic core of quantum mechanics, but in the years following World War II he offered a powerful new way of thinking about the theory. From the standpoint of numerical predictions, Feynman's perspective agrees exactly with all that went before. But its formulation is quite different. Let's describe it in the context of the electron two-slit experiment.
The troubling thing about Figure 4.8 is that we envision each electron as passing through either the left slit or the right slit and therefore we expect the union of Figures 4.4 and 4.5, as in Figure 4.6, to represent the resulting data accurately. An electron that passes through the right slit should not care that there also happens to be a left slit, and vice versa. But somehow it does. The interference pattern generated requires an overlapping and an intermingling between something sensitive to both slits, even if we fire electrons one by one. Schrödinger, de Broglie, and Born explained this phenomenon by associating a probability wave to each electron. Like the water waves in Figure 4.7, the electron's probability wave "sees" both slits and is subject to the same kind of interference from intermingling. Places where the probability wave is augmented by the intermingling, like the places of significant jostling in Figure 4.7, are locations where the electron is likely to be found; places where the probability wave is diminished by the intermingling, like the places of minimal or no jostling in Figure 4.7, are locations where the electron is unlikely or never to be found. Electrons hit the phosphorescent screen one by one, distributed according to this probability profile, and thereby build up an interference pattern like that in Figure 4.8.
Feynman took a different tack. He challenged the basic classical assumption that each electron either goes through the left slit or the right slit. You might think this to be such a basic property of how things work that challenging it is fatuous. After all, can't you look in the region between the slits and the phosphorescent screen to determine through which slit each electron passes? You can. But now you have changed the experiment. To see the electron you must do something to it—for instance, you can shine light on it, that is, bounce photons off it. Now, on everyday scales photons act as negligible little probes that bounce off trees, paintings, and people with essentially no effect on the state of motion of these comparatively large material bodies. But electrons are little wisps of matter. Regardless of how gingerly you carry out your determination of the slit through which it passed, photons that bounce off the electron necessarily affect its subsequent motion. And this change in motion changes the results of our experiment. If you disturb the experiment just enough to determine the slit through which each electron passes, experiments show that the results change from that of Figure 4.8 and become like that of Figure 4.6! The quantum world ensures that once it has been established that each electron has gone through either the left slit or the right slit, the interference between the two slits disappears.
And so Feynman was justified in leveling his challenge since—although our experience in the world seems to require that each electron pass through one or the other of the slits—by the late 1920s physicists realized that any attempt to verify this seemingly basic quality of reality ruins the experiment.
Feynman proclaimed that each electron that makes it through to the phosphorescent screen actually goes through both slits. It sounds crazy, but hang on: Things get even more wild. Feynman argued that in traveling from the source to a given point on the phosphorescent screen each individual electron actually traverses every possible trajectory simultaneously; a few of the trajectories are illustrated in Figure 4.10. It goes in a nice orderly way through the left slit. It simultaneously also goes in a nice orderly way through the right slit. It heads toward the left slit, but suddenly changes course and heads through the right. It meanders back and forth, finally passing through the left slit. It goes on a long journey to the Andromeda galaxy before turning back and passing through the left slit on its way to the screen. And on and on it goes—the electron, according to Feynman, simultaneously "sniffs" out every possible path connecting its starting location with its final destination.
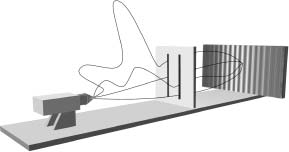
Figure 4.10 According to Feynman's formulation of quantum mechanics, particles must be viewed as travelling from one location to another along every possible path. Here, a few of the infinity of trajectories for a single electron travelling from the source to the phosphorescent screen are shown. Notice that this one electron actually goes through both slits.
Feynman showed that he could assign a number to each of these paths in such a way that their combined average yields exactly the same result for the probability calculated using the wave-function approach. And so from Feynman's perspective no probability wave needs to be associated with the electron. Instead, we have to imagine something equally if not more bizarre. The probability that the electron—always viewed as a particle through and through—arrives at any chosen point on the screen is built up from the combined effect of every possible way of getting there. This is known as Feynman's "sum-over-paths" approach to quantum mechanics.7
At this point your classical upbringing is balking: How can one electron simultaneously take different paths—and no less than an infinite number of them? This seems like a defensible objection, but quantum mechanics—the physics of our world—requires that you hold such pedestrian complaints in abeyance. The result of calculations using Feynman's approach agree with those of the wave function method, which agree with experiments. You must allow nature to dictate what is and what is not sensible. As Feynman once wrote, "[Quantum mechanics] describes nature as absurd from the point of view of common sense. And it fully agrees with experiment. So I hope you can accept nature as She is—absurd."8
But no matter how absurd nature is when examined on microscopic scales, things must conspire so that we recover the familiar prosaic happenings of the world experienced on everyday scales. To this end, Feynman showed that if you examine the motion of large objects—like baseballs, airplanes, or planets, all large in comparison with subatomic particles—his rule for assigning numbers to each path ensures that all paths but one cancel each other out when their contributions are combined. In effect, only one of the infinity of paths matters as far as the motion of the object is concerned. And this trajectory is precisely the one emerging from Newton's laws of motion. This is why in the everyday world it seems to us that objects—like a ball tossed in the air—follow a single, unique, and predictable trajectory from their origin to their destination. But for microscopic objects, Feynman's rule for assigning numbers to paths shows that many different paths can and often do contribute to an object's motion. In the double-slit experiment, for example, some of these paths pass through different slits, giving rise to the interference pattern observed. In the microscopic realm we therefore cannot assert that an electron passes through only one slit or the other. The interference pattern and Feynman's alternative formulation of quantum mechanics emphatically attest to the contrary.
Just as we may find that varying interpretations of a book or a film can be more or less helpful in aiding our understanding of different aspects of the work, the same is true of the different approaches to quantum mechanics. Although their predictions always agree completely, the wave function approach and Feynman's sum-over-paths approach give us different ways of thinking about what's going on. As we shall see later on, for some applications, one or the other approach can provide an invaluable explanatory framework.
Quantum Weirdness
By now you should have some sense of the dramatically new way that the universe works according to quantum mechanics. If you have not as yet fallen victim to Bohr's dizziness dictum, the quantum weirdness we now discuss should at least make you feel a bit lightheaded.
Even more so than with the theories of relativity, it is hard to embrace quantum mechanics viscerally—to think like a miniature person born and raised in the microscopic realm. There is, though, one aspect of the theory that can act as a guidepost for your intuition, as it is the hallmark feature that fundamentally differentiates quantum from classical reasoning. It is the uncertainty principle, discovered by the German physicist Werner Heisenberg in 1927.
This principle grows out of an objection that may have occurred to you earlier. We noted that the act of determining the slit through which each electron passes (its position) necessarily disturbs its subsequent motion (its velocity). But just as we can assure ourselves of someone's presence either by gently touching them or by giving them an overzealous slap on the back, why can't we determine the electron's position with an "ever gentler" light source in order to have an ever decreasing impact on its motion? From the standpoint of nineteenth-century physics we can. By using an ever dimmer lamp (and an ever more sensitive light detector) we can have a vanishingly small impact on the electron's motion. But quantum mechanics itself illuminates a flaw in this reasoning. As we turn down the intensity of the light source we now know that we are decreasing the number of photons it emits. Once we get down to emitting individual photons we cannot dim the light any further without actually turning it off. There is a fundamental quantum-mechanical limit to the "gentleness" of our probe. And hence, there is always a minimal disruption that we cause to the electron's velocity through our measurement of its position.
Well, that's almost correct. Planck's law tells us that the energy of a single photon is proportional to its frequency (inversely proportional to its wavelength). By using light of lower and lower frequency (larger and larger wavelength) we can therefore produce ever gentler individual photons. But here's the catch. When we bounce a wave off of an object, the information we receive is only enough to determine the object's position to within a margin of error equal to the wave's wavelength. To get an intuitive feel for this important fact, imagine trying to pinpoint the location of a large, slightly submerged rock by the way it affects passing ocean waves. As the waves approach the rock, they form a nice orderly train of one up and-down wave cycle followed by another. After passing by the rock, the individual wave cycles are distorted—the telltale sign of the submerged rock's presence. But like the finest set of tick marks on a ruler, the individual up-and-down wave cycles are the finest units making up the wave-train, and therefore by examining solely how they are disrupted we can determine the rock's location only to within a margin of error equal to the length of the wave cycles, that is, the wave's wavelength. In the case of light, the constituent photons are, roughly speaking, the individual wave cycles (with the height of the wave cycles being determined by the number of photons); a photon, therefore, can be used to pinpoint an object's location only to within a precision of one wavelength.
And so we are faced with a quantum-mechanical balancing act. If we use high-frequency (short wavelength) light we can locate an electron with greater precision. But high-frequency photons are very energetic and therefore sharply disturb the electron's velocity. If we use low-frequency (long wavelength) light we minimize the impact on the electron's motion, since the constituent photons have comparatively low energy, but we sacrifice precision in determining the electron's position. Heisenberg quantified this competition and found a mathematical relationship between the precision with which one measures the electron's position and the precision with which one measures its velocity. He found—in line with our discussion—that each is inversely proportional to the other: Greater precision in a position measurement necessarily entails greater imprecision in a velocity measurement, and vice versa. And of utmost importance, although we have tied our discussion to one particular means for determining the electron's whereabouts, Heisenberg showed that the trade-off between the precision of position and velocity measurements is a fundamental fact that holds true regardless of the equipment used or the procedure employed. Unlike the framework of Newton or even of Einstein, in which the motion of a particle is described by giving its location and its velocity, quantum mechanics shows that at a microscopic level you cannot possibly know both of these features with total precision. Moreover, the more precisely you know one, the less precisely you know the other. And although we have described this for electrons, the ideas directly apply to all constituents of nature.
Einstein tried to minimize this departure from classical physics by arguing that although quantum reasoning certainly does appear to limit one's knowledge of the position and velocity, the electron still has a definite position and velocity exactly as we have always thought. But during the last couple of decades theoretical progress spearheaded by the late Irish physicist John Bell and the experimental results of Alain Aspect and his collaborators have shown convincingly that Einstein was wrong. Electrons—and everything else for that matter—cannot be described as simultaneously being at such-and-such location andhaving such-and-such speed. Quantum mechanics shows that not only could such a statement never be experimentally verified—as explained above—but it directly contradicts other, more recently established experimental results.
In fact, if you were to capture a single electron in a big, solid box and then slowly crush the sides to pinpoint its position with ever greater precision, you would find the electron getting more and more frantic. Almost as if it were overcome with claustrophobia, the electron will go increasingly haywire—bouncing off of the walls of the box with increasingly frenetic and unpredictable speed. Nature does not allow its constituents to be cornered. In the H-Bar, where we imagine h to be much larger than in the real world, thereby making everyday objects directly subject to quantum effects, the ice cubes in George's and Gracie's drinks frantically rattle around as they too suffer from quantum claustrophobia. Although the H-Bar is a fantasyland—in reality, h is terribly small—precisely this kind of quantum claustrophobia is a pervasive feature of the microscopic realm. The motion of microscopic particles becomes increasingly wild when they are examined and confined to ever smaller regions of space.
The uncertainty principle also gives rise to a striking effect known as quantum tunneling. If you fire a plastic pellet against a ten-foot-thick concrete wall, classical physics confirms what your instincts tell you will happen: The pellet will bounce back at you. The reason is that the pellet simply does not have enough energy to penetrate such a formidable obstacle. But at the level of fundamental particles, quantum mechanics shows unequivocally that the wave functions—that is, the probability waves—of the particles making up the pellet all have a tiny piece that spills out through the wall. This means that there is a small—but not zero—chance that the pellet actually can penetrate the wall and emerge on the other side. How can this be? The reason comes down, once again, to Heisenberg's uncertainty principle.
To see this, imagine that you are completely destitute and suddenly learn that a distant relative has passed on in a far-off land, leaving you a tremendous fortune to claim. The only problem is that you don't have the money to buy a plane ticket to get there. You explain the situation to your friends: if only they will allow you to surmount the barrier between you and your new fortune by temporarily lending you the money for a ticket, you can pay them back handsomely after your return. But no one has the money to lend. You remember, though, that an old friend of yours works for an airline and you implore him with the same request. Again, he cannot afford to lend you the money but he does offer a solution. The accounting system of the airline is such that if you wire the ticket payment within 24 hours of arrival at your destination, no one will ever know that it was not paid for prior to departure. In this way you are able to claim your inheritance.
The accounting procedures of quantum mechanics are quite similar. Just as Heisenberg showed that there is a trade-off between the precision of measurements of position and velocity, he also showed that there is a similar trade-off in the precision of energy measurements and how long one takes to do the measurement. Quantum mechanics asserts that you can't say that a particle has precisely such-and-such energy at precisely such-and-such moment in time. Ever increasing precision of energy measurements require ever longer durations to carry them out. Roughly speaking, this means that the energy a particle has can wildly fluctuate so long as this fluctuation is over a short enough time scale. So, just as the accounting system of the airline "allows" you to "borrow" the money for a plane ticket provided you pay it back quickly enough, quantum mechanics allows a particle to "borrow" energy so long as it can relinquish it within a time frame determined by Heisenberg's uncertainty principle.
The mathematics of quantum mechanics shows that the greater the energy barrier, the lower the probability that this creative microscopic accounting will actually occur. But for microscopic particles facing a concrete slab, they can and sometimes do borrow enough energy to do what is impossible from the standpoint of classical physics—momentarily penetrate and tunnel through a region that they do not initially have enough energy to enter. As the objects we study become increasingly complicated, consisting of more and more particle constituents, such quantum tunneling can still occur, but it becomes very unlikely since all of the individual particles must be lucky enough to tunnel together. But the shocking episodes of George's disappearing cigar, of an ice cube passing right through the wall of a glass, and of George and Gracie's passing right through a wall of the bar, can happen. In a fantasyland such as the H-Bar, in which we imagine that h is large, such quantum tunneling is commonplace. But the probability rules of quantum mechanics—and, in particular, the actual smallness of h in the real world—show that if you walked into a solid wall every second, you would have to wait longer than the current age of the universe to have a good chance of passing through it on one of your attempts. With eternal patience (and longevity), though, you could—sooner or later—emerge on the other side.
The uncertainty principle captures the heart of quantum mechanics. Features that we normally think of as being so basic as to be beyond question—that objects have definite positions and speeds and that they have definite energies at definite moments—are now seen as mere artifacts of Planck's constant being so tiny on the scales of the everyday world. Of prime importance is that when this quantum realization is applied to the fabric of spacetime, it shows fatal imperfections in the "stitches of gravity" and leads us to the third and primary conflict physics has faced during the past century.