The Elegant Universe: Superstrings, Hidden Dimensions, and the Quest for the Ultimate Theory - Brian Greene (2010)
Part II. The Dilemma of Space, Time, and the Quanta
Chapter 2. Space, Time, and the Eye of the Beholder
In June 1905, twenty-six-year-old Albert Einstein submitted a technical article to the German Annals of Physics in which he came to grips with a paradox about light that had first troubled him as a teenager, some ten years earlier. Upon turning the final page of Einstein's manuscript, the editor of the journal, Max Planck, realized that the accepted scientific order had been overthrown. Without hoopla or fanfare, a patent clerk from Bern, Switzerland, had completely overturned the traditional notions of space and time and replaced them with a new conception whose properties fly in the face of everything we are familiar with from common experience.
The paradox that had troubled Einstein for a decade was this. In the mid-1800s, after a close study of the experimental work of the English physicist Michael Faraday, the Scottish physicist James Clerk Maxwell succeeded in uniting electricity and magnetism in the framework of the electromagnetic field. If you've ever been on a mountaintop just before a severe thunderstorm or stood close to a Van de Graaf generator, you have a visceral sense of what an electromagnetic field is, because you've felt it. In case you haven't, it is somewhat like a tide of electric and magnetic lines of force that permeate a region of space through which they pass. When you sprinkle iron filings near a magnet, for example, the orderly pattern they form traces out some of the invisible lines of magnetic force. When you take off a wool sweater on an especially dry day and hear a crackling sound and perhaps feel a momentary shock or two, you are witnessing evidence of electric lines of force generated by electric charges swept up by the fibers in your sweater. Beyond uniting these and all other electric and magnetic phenomena in one mathematical framework, Maxwell's theory showed—quite unexpectedly—that electromagnetic disturbances travel at a fixed and never-changing speed, a speed that turns out to equal that of light. From this, Maxwell realized that visible light itself is nothing but a particular kind of electromagnetic wave, one that is now understood to interact with chemicals in the retina, giving rise to the sensation of sight. Moreover (and this is crucial), Maxwell's theory also showed that all electromagnetic waves—visible light among them—are the epitome of the peripatetic traveler. They never stop. They never slow down. Light always travels at light speed.
All is well and good until we ask, as the sixteen-year-old Einstein did, What happens if we chase after a beam of light, at light speed? Intuitive reasoning, rooted in Newton's laws of motion, tells us that we will catch up with the light waves and so they will appear stationary; light will stand still. But according to Maxwell's theory, and all reliable observations, there is simply no such thing as stationary light: no one has ever held a stationary clump of light in the palm of his or her hand. Hence the problem. Luckily, Einstein was unaware that many of the world's leading physicists were struggling with this question (and were heading down many a spurious path) and pondered the paradox of Maxwell and Newton largely in the pristine privacy of his own thoughts.
In this chapter we discuss how Einstein resolved the conflict through his special theory of relativity, and in so doing forever changed our conceptions of space and time. It is perhaps surprising that the essential concern of special relativity is to understand precisely how the world appears to individuals, often called "observers," who are moving relative to one another. At first, this might seem to be an intellectual exercise of minimal importance. Quite the contrary: In the hands of Einstein, with his imaginings of observers chasing after light beams, there are profound implications to grasping fully how even the most mundane situations appear to individuals in relative motion.
Intuition and Its Flaws
Common experience highlights certain ways in which observations by such individuals differ. Trees alongside a highway, for example, appear to be moving from the viewpoint of a driver but appear stationary to a hitchhiker sitting on a guardrail. Similarly, the dashboard of the automobile does not appear to be moving from the viewpoint of the driver (one hopes!), but like the rest of the car, it does appear to be moving from the viewpoint of the hitchhiker. These are such basic and intuitive properties of how the world works that we hardly take note of them.
Special relativity, however, proclaims that the differences in observations between two such individuals are more subtle and profound. It makes the strange claim that observers in relative motion will have different perceptions of distance and of time. This means, as we shall see, that identical wristwatches worn by two individuals in relative motion will tick at different rates and hence will not agree on the amount of time that elapses between chosen events. Special relativity demonstrates that this statement does not slander the accuracy of the wristwatches involved; rather, it is a true statement about time itself.
Similarly, observers in relative motion carrying identical tape measures will not agree on the lengths of distances measured. Again, this is not due to inaccuracies in the measuring devices or to errors in how they are used. The most accurate measuring devices in the world confirm that space and time—as measured by distances and durations—are not experienced identically by everyone. In the precise way delineated by Einstein, special relativity resolves the conflict between our intuition about motion and the properties of light, but there is a price: individuals who are moving with respect to each other will not agree on their observations of either space or time.
It has been almost a century since Einstein informed the world of his dramatic discovery, yet most of us still see space and time in absolute terms. Special relativity is not in our bones—we do not feel it. Its implications are not a central part of our intuition. The reason for this is quite simple: The effects of special relativity depend upon how fast one moves, and at the speeds of cars, planes, or even space shuttles, these effects are minuscule. Differences in perceptions of space and of time between individuals planted on the earth and those traveling in cars or planes do occur, but they are so small that they go unnoticed. However, were one to take a trip in a futuristic space vehicle traveling at a substantial fraction of light speed, the effects of relativity would become plainly obvious. This, of course, is still in the realm of science fiction. Nevertheless, as we shall discuss in later sections, clever experiments allow clear and precise observation of the relative properties of space and time predicted by Einstein's theory.
To get a sense of the scales involved, imagine that the year is 1970 and big, fast cars are in. Slim, having just spent all his savings on a new Trans Am, goes with his brother Jim to the local drag strip to give the car the kind of test-drive forbidden by the dealer. After revving up the car, Slim streaks down the mile-long strip at 120 miles per hour while Jim stands on the sideline and times him. Wanting an independent confirmation, Slim also uses a stopwatch to determine how long it takes his new car to traverse the track. Prior to Einstein's work, no one would have questioned that if both Slim and Jim have properly functioning stopwatches, each will measure the identical elapsed time. But according to special relativity, while Jim will measure an elapsed time of 30 seconds, Slim's stopwatch will record an elapsed time of 29.99999999999952 seconds—a tiny bit less. Of course, this difference is so small that it could be detected only through a measurement whose accuracy is well beyond the capacity of hand-held stopwatches run by the press of a finger, Olympic-quality timing systems, or even the most precisely engineered atomic clocks. It is no wonder that our everyday experiences do not reveal the fact that the passage of time depends upon our state of motion.
There will be a similar disagreement on measurements of length. For example, on another test run Jim uses a clever trick to measure the length of Slim's new car: he starts his stopwatch just as the front of the car reaches him and he stops it just as the back of the car passes. Since Jim knows that Slim is speeding along at 120 miles per hour, he is able to figure out the length of the car by multiplying this speed by the elapsed time on his stopwatch. Again, prior to Einstein, no one would have questioned that the length Jim measures in this indirect way would agree exactly with the length Slim carefully measured when the car sat motionless on the showroom floor. Special relativity proclaims, on the contrary, that if Slim and Jim carry out precise measurements in this manner and Slim finds the car to be, say, exactly 16 feet long, then Jim's measurement will find the car to be 15.99999999999974 feet long—a tiny bit less. As with the measurement of time, this is such a minuscule difference that ordinary instruments are just not accurate enough to detect it.
Although the differences are extremely small, they show a fatal flaw in the commonly held conception of universal and immutable space and time. As the relative velocity of individuals such as Slim and Jim gets larger, this flaw becomes increasingly apparent. To achieve noticeable differences, the speeds involved must be a sizeable fraction of the maximum possible speed—that of light—which Maxwell's theory and experimental measurements show to be about 186,000 miles per second, or about 670 million miles per hour. This is fast enough to circle the earth more than seven times in a second. If Slim, for example, were to travel not at 120 miles per hour but at 580 million miles per hour (about 87 percent of light speed), the mathematics of special relativity predicts that Jim would measure the length of the car to be about eight feet, which is substantially different from Slim's measurement (as well as the specifications in the owner's manual). Similarly, the time to traverse the drag strip according to Jim will be about twice as long as the time measured by Slim.
Since such enormous speeds are far beyond anything currently attainable, the effects of "time dilation" and "Lorentz contraction," as these phenomena are technically called, are extremely small in day-to-day life. If we happened to live in a world in which things typically traveled at speeds close to that of light, these properties of space and time would be so completely intuitive—since we would experience them constantly—that they would deserve no more discussion than the apparent motion of trees on the side of the road mentioned at the outset of this chapter. But since we don't live in such a world, these features are unfamiliar. As we shall see, understanding and accepting them requires that we subject our worldview to a thorough makeover.
The Principle of Relativity
There are two simple yet deeply rooted structures that form the foundation of special relativity. As mentioned, one concerns properties of light; we shall discuss this more fully in the next section. The other is more abstract. It is concerned not with any specific physical law but rather with all physical laws, and is known as the principle of relativity. The principle of relativity rests on a simple fact: Whenever we discuss speed or velocity (an object's speed and its direction of motion), we must specify precisely who or what is doing the measuring. Understanding the meaning and importance of this statement is easily accomplished by contemplating the following situation.
Imagine that George, who is wearing a spacesuit with a small, red flashing light, is floating in the absolute darkness of completely empty space, far away from any planets, stars, or galaxies. From George's perspective, he is completely stationary, engulfed in the uniform, still blackness of the cosmos. Off in the distance, George catches sight of a tiny, green flashing light that appears to be coming closer and closer. Finally, it gets close enough for George to see that the light is attached to the spacesuit of another space-dweller, Gracie, who is slowly floating by. She waves as she passes, as does George, and she recedes into the distance. This story can be told with equal validity from Gracie's perspective. It begins in the same manner with Gracie completely alone in the immense still darkness of outer space. Off in the distance, Gracie sees a red flashing light, which appears to be coming closer and closer. Finally, it gets close enough for Gracie to see that it is attached to the spacesuit of another being, George, who is slowly floating by. He waves as he passes, as does Gracie, and he recedes into the distance.
The two stories describe one and the same situation from two distinct but equally valid points of view. Each observer feels stationary and perceives the other as moving. Each perspective is understandable and justifiable. As there is symmetry between the two space-dwellers, there is, on quite fundamental grounds, no way of saying one perspective is "right" and the other "wrong." Each perspective has an equal claim on truth.
This example captures the meaning of the principle of relativity: The concept of motion is relative. We can speak about the motion of an object, but only relative to or by comparison with another. There is thus no meaning to the statement "George is traveling at 10 miles per hour," as we have not specified any other object for comparison. There is meaning to the statement "George is traveling at 10 miles per hour past Gracie," as we have now specified Gracie as the benchmark. As our example shows, this last statement is completely equivalent to "Gracie is traveling at 10 miles per hour past George (in the opposite direction)." In other words, there is no "absolute" notion of motion. Motion is relative.
A key element of this story is that neither George nor Gracie is being pushed, pulled, or in any other way acted upon by a force or influence that could disturb their serene state of force-free, constant-velocity motion. Thus, a more precise statement is that force-free motion has meaning only by comparison with other objects. This is an important clarification, because if forces are involved, they cause changes in the velocity of the observers—changes to their speed and/or their direction of motion—and these changes can be felt. For instance, if George were wearing a jet-pack firing away from his back, he would definitely feel that he was moving. This feeling is intrinsic. If the jet-pack is firing away, George knows he is moving, even if his eyes are closed and therefore can make no comparisons with other objects. Even without such comparisons, he would no longer claim that he was stationary while "the rest of the world was moving by him." Constant-velocity motion is relative; not so for non-constant-velocity motion, or, equivalently, accelerated motion. (We will re-examine this statement in the next chapter when we take up accelerated motion and discuss Einstein's general theory of relativity.)
Setting these stories in the darkness of empty space aids understanding by removing such familiar things as streets and buildings, which we typically, although unjustifiably, accord the special status of "stationary." Nonetheless, the same principle applies to terrestrial settings, and in fact is commonly experienced.1 For example, imagine that after you have fallen asleep on a train, you awake just as your train is passing another on adjacent parallel tracks. With your view through the window completely blocked by the other train, thereby preventing you from seeing any other objects, you may temporarily be uncertain as to whether your train is moving, the other train is moving, or both. Of course, if your train shakes or jostles, or if the train changes direction by rounding a bend, you can feel that you are moving. But if the ride is perfectly smooth—if the train's velocity remains constant—you will observe relative motion between the trains without being able to tell for certain which is moving.
Let's take this one step further. Imagine you are on such a train and that you pull down the shades so that the windows are fully covered. Without the ability to see anything outside your own compartment, and assuming that the train moves at absolutely constant velocity, there will be no way for you to determine your state of motion. The compartment around you will look precisely the same regardless of whether the train is sitting still on the tracks or moving at high speed. Einstein formalized this idea, one that actually goes back to insights of Galileo, by proclaiming that it is impossible for you or any fellow traveler to perform an experiment within the closed compartment that will determine whether or not the train is moving. This again captures the principle of relativity: since all force-free motion is relative, it has meaning only by comparison with other objects or individuals also undergoing force-free motion. There is no way for you to determine anything about your state of motion without making some direct or indirect comparison with "outside" objects. There simply is no notion of "absolute" constant-velocity motion; only comparisons have any physical meaning.
In fact, Einstein realized that the principle of relativity makes an even grander claim: the laws of physics—whatever they may be—must be absolutely identical for all observers undergoing constant-velocity motion. If George and Gracie are not just floating solo in space, but, rather, are each conducting the same set of experiments in their respective floating space-stations, the results they find will be identical. Once again, each is perfectly justified in believing that his or her station is at rest, even though the two stations are in relative motion. If all of their equipment is identical, there is nothing distinguishing the two experimental setups—they are completely symmetric. The laws of physics that each deduces from the experiments will likewise be identical. Neither they nor their experiments can feel—that is, depend upon in any way—constant-velocity travel. It is this simple concept that establishes complete symmetry between such observers; it is this concept that is embodied in the principle of relativity. We shall shortly make use of this principle to profound effect.
The Speed of Light
The second key ingredient in special relativity has to do with light and properties of its motion. Contrary to our claim that there is no meaning to the statement "George is traveling at 10 miles per hour" without a specified benchmark for comparison, almost a century of effort by a series of dedicated experimental physicists has shown that any and all observers will agree that light travels at 670 million miles per hour regardless of benchmarks for comparison.
This fact has required a revolution in our view of the universe. Let's first gain an understanding of its meaning by contrasting it with similar statements applied to more common objects. Imagine it's a nice, sunny day and you go outside to play a game of catch with a friend. For a while, you both leisurely throw the ball back and forth with a speed of, say, 20 feet per second, when suddenly an unexpected electrical storm stirs overhead, sending you both running for cover. After it passes, you rejoin to resume your game of catch but you notice that something has changed. Your friend's hair has become wild and spiky, and her eyes have grown severe and crazed. When you look at her hand, you are stunned to see that she is no longer planning to play catch with a baseball, but instead is about to toss you a hand grenade. Understandably, your enthusiasm for playing catch diminishes substantially; you turn to run. When your companion throws the grenade, it will still fly toward you, but because you are running, the speed with which it approaches you will be less than 20 feet per second. In fact, common experience tells us that if you can run at, say, 12 feet per second then the hand-grenade will approach you at (20-12 =) 8 feet per second. As another example, if you are in the mountains and an avalanche of snow is rumbling toward you, your inclination is to turn and run because this will cause the speed with which the snow approaches you to decrease—and this, generally, is a good thing. Again, a stationary individual perceives the speed of the approaching snow to be greater than that perceived by someone in retreat.
Now, let's compare these basic observations about baseballs, grenades, and avalanches to those about light. To make the comparisons tighter, think about a light beam as composed of tiny "packets" or "bundles" known as photons (a feature of light we will discuss more fully in Chapter 4). When we turn on a flashlight or a laser beam we are, in effect, shooting a stream of photons in whatever direction we point the device. As we did for grenades and avalanches, let's consider how the motion of a photon appears to someone who is moving. Imagine that your crazed friend has swapped her grenade for a powerful laser. If she fires the laser toward you—and if you had the appropriate measuring equipment—you would find that the speed of approach of the photons in the beam is 670 million miles per hour. But what if you run away, as you did when faced with the prospect of playing catch with a hand grenade? What speed will you now measure for the approaching photons? To make things more compelling, imagine that you can hitch a ride on the starship Enterprise and zip away from your friend at, say, 100 million miles per hour. Following the reasoning based on the traditional Newtonian worldview, since you are now speeding away, you would expect to measure a slower speed for the oncoming photons. Specifically, you would expect to find them approaching you at (670 million miles per hour -100 million miles per hour =) 570 million miles per hour.
Mounting evidence from a variety of experiments dating back as far as the 1880s, as well as careful analysis and interpretation of Maxwell's electromagnetic theory of light, slowly convinced the scientific community that, in fact, this is not what you will see. Even though you are retreating, you will still measure the speed of the approaching photons as 670 million miles per hour, not a bit less. Although at first it sounds completely ridiculous, unlike what happens if one runs from an oncoming baseball, grenade, or avalanche, the speed of approaching photons is always 670 million miles per hour. The same is true if you run toward oncoming photons or chase after them—their speed of approach or recession is completely unchanged; they still appear to travel at 670 million miles per hour. Regardless of relative motion between the source of photons and the observer, the speed of light is always the same.2
Technological limitations are such that the "experiments" with light, as described, cannot actually be carried out. However, comparable experiments can. For instance, in 1913 the Dutch physicist Willem de Sitter suggested that fast-moving binary stars (two stars that orbit one another) could be used to measure the effect of a moving source on the speed of light. Various experiments of this sort over the past eight decades have verified that the speed of light received from a moving star is the same as that from a stationary star—670 million miles per hour—to within the impressive accuracy of ever more refined measuring devices. Moreover, a wealth of other detailed experiments has been carried out during the past century—experiments that directly measure the speed of light in various circumstances, as well as test many of the implications arising from this characteristic of light, as discussed shortly—and all have confirmed the constancy of the speed of light.
If you find this property of light hard to swallow, you are not alone. At the turn of the century physicists went to great length to refute it. They couldn't. Einstein, to the contrary, embraced the constancy of the speed of light, for here was the answer to the conflict that had troubled him since he was a teenager: No matter how hard you chase after a light beam, it still retreats from you at light speed. You can't make the apparent speed with which light departs one iota less than 670 million miles per hour, let alone slow it down to the point of appearing stationary. Case closed. But this triumph over paradox was no small victory. Einstein realized that the constancy of light's speed spelled the downfall of Newtonian physics.
Truth and Consequences
Speed is a measure of how far an object can travel in a given duration of time. If we are in a car going 65 miles per hour, this means of course that we will travel 65 miles if we persist in this state of motion for an hour. Phrased in this manner, speed is a rather mundane concept, and you may wonder about the fuss we have made regarding the speed of baseballs, snowballs, and photons. However, let's note that distance is a notion about space—in particular it is a measure of how much space there is between two points. Also note that duration is a notion about time—how much time elapses between two events. Speed, therefore, is intimately connected with our notions of space and time. When we phrase it this way, we see that any experimental fact that defies our common conception about speed, such as the constancy of the speed of light, has the potential to defy our common conceptions of space and time themselves. It is for this reason that the strange fact about the speed of light deserves detailed scrutiny—scrutiny given to it by Einstein, leading him to remarkable conclusions.
The Effect on Time: Part I
With minimal effort, we can make use of the constancy of the speed of light to show that the familiar everyday conception of time is plain wrong. Imagine that the leaders of two warring nations, sitting at opposite ends of a long negotiating table, have just concluded an agreement for a cease-fire, but neither wants to sign the accord before the other. The secretary-general of the United Nations comes up with a brilliant resolution. A light bulb, initially turned off, will be placed midway between the two presidents. When it is turned on, the light it emits will reach each of the presidents simultaneously, since they are equidistant from the bulb. Each president agrees to sign a copy of the accord when he or she sees the light. The plan is carried out and the agreement is signed to the satisfaction of both sides.
Flushed with success, the secretary-general makes use of the same approach with two other embattled nations that have also reached a peace agreement. The only difference is that the presidents involved in this negotiation are sitting at opposite ends of a table inside a train traveling along at constant velocity. Fittingly, the president of Forwardland is facing in the direction of the train's motion while the president of Backwardland is facing in the opposite direction. Familiar with the fact that the laws of physics take precisely the same form regardless of one's state of motion so long as this motion is unchanging, the secretary-general takes no heed of this difference, and carries out the light bulb-initiated signing ceremony as before. Both presidents sign the agreement, and along with their entourage of advisers, celebrate the end of hostilities.
Just then, word arrives that fighting has broken out between people from each country who had been watching the signing ceremony from the platform outside the moving train. All those on the negotiation train are dismayed to hear that the reason for the renewed hostilities is the claim by people from Forwardland that they have been duped, as their president signed the agreement before the president of Backwardland. As everyone on the train—from both sides—agrees that the accord was signed simultaneously, how can it be that the outside observers watching the ceremony think otherwise?
Let's consider in more detail the perspective of an observer on the platform. Initially the bulb on the train is dark, and then at a particular moment it illuminates, sending beams of light speeding toward both presidents. From the perspective of a person on the platform, the president of Forwardland is heading toward the emitted light while the president of Backwardland is retreating. This means, to the platform observers, that the light beam does not have to travel as far to reach the president of Forwardland, who moves toward the approaching light, as it does to reach the president of Backwardland, who moves away from it. This is not a statement about the speed of the light as it travels toward the two presidents—we have already noted that regardless of the state of motion of the source or the observer, the speed of light is always the same. Instead, we are describing only how far, from the vantage point of the platform observers, the initial flash of light must travel to reach each of the presidents. Since this distance is less for the president of Forwardland than it is for the president of Backwardland, and since the speed of light toward each is the same, the light will reach the president of Forwardland first. This is why the citizens of Forwardland claim to have been duped.
When CNN broadcasts the eyewitness account, the secretary-general, the two presidents, and all of their advisers can't believe their ears. They all agree that the light bulb was secured firmly, exactly midway between the two presidents and that therefore, without further ado, the light it emitted traveled the same distance to reach each of them. Since the speed of the emitted light to the left and to the right is the same, they believe, and in fact observed, that the light clearly reached each president simultaneously.
Who is right, those on or off the train? The observations of each group and their supporting explanations are impeccable. The answer is that both are right. Like our two space inhabitants George and Gracie, each perspective has an equal claim on truth. The only subtlety here is that the respective truths seem to be contradictory. An important political issue is at stake: Did the presidents sign the agreement simultaneously? The observations and reasoning above ineluctably lead us to the conclusion that according to those on the train they did while according to those on the platform they did not. In other words, things that are simultaneous from the viewpoint of some observers will not be simultaneous from the viewpoint of others, if the two groups are in relative motion.
This is a startling conclusion. It is one of the deepest insights into the nature of reality ever discovered. Nevertheless, if long after you set down this book you remember nothing of this chapter except for the ill-fated attempt at detente, you will have retained the essence of Einstein's discovery. Without highbrow mathematics or a convoluted chain of logic, this completely unexpected feature of time follows directly from the constancy of the speed of light, as the scenario illustrates. Notice that if the speed of light were not constant but behaved according to our intuition based on slow-moving baseballs and snowballs, the platform observers would agree with those on the train. A platform observer would still claim that the photons have to travel farther to reach the president of Backwardland than they do to reach the president of Forwardland. However, usual intuition implies that the light approaching the president of Backwardland would be moving more quickly, having received a "kick" from the forward-moving train. Similarly, these observers would see that the light approaching the president of Forwardland would be moving more slowly, being "dragged" back by the train's motion. When these (erroneous) effects were considered, the observers on the platform would see that that the light beams reached each president simultaneously. However, in the real world light does not speed up or slow down, it cannot be kicked to a higher speed or dragged to a slower one. Platform observers will therefore justifiably claim that the light reached the president of Forwardland first.
The constancy of the speed of light requires that we give up the age-old notion that simultaneity is a universal concept that everyone, regardless of their state of motion, agrees upon. The universal clock previously envisioned to dispassionately tick off identical seconds here on earth and on Mars and on Jupiter and in the Andromeda galaxy and in each and every nook and cranny of the cosmos does not exist. On the contrary, observers in relative motion will not agree on which events occur at the same time. Once again, the reason that this conclusion—a bona fide characteristic of the world we inhabit—is so unfamiliar is that the effects are extremely small when the speeds involved are those commonly encountered in everyday experience. If the negotiating table were 100 feet long and the train were moving at 10 miles per hour, platform observers would "see" that the light reached the president of Forwardland about a millionth of a billionth of a second before it reached the president of Backwardland. Although this represents a genuine difference, it is so tiny that it cannot be detected directly by human senses. If the train were moving considerably faster, say at 600 million miles per hour, from the perspective of someone on the platform the light would take almost 20 times as long to reach the president of Backwardland compared with the time to reach the president of Forwardland. At high speeds, the startling effects of special relativity become increasingly pronounced.
The Effect on Time: Part II
It is difficult to give an abstract definition of time—attempts to do so often wind up invoking the word "time" itself, or else go through linguistic contortions simply to avoid doing so. Rather than proceeding down such a path, we can take a pragmatic viewpoint and define time to be that which is measured by clocks. Of course, this shifts the burden of definition to the word "clock"; here we can somewhat loosely think of a clock as a device that undergoes perfectly regular cycles of motion. We will measure time by counting the number of cycles our clock goes through. A familiar clock such as a wristwatch meets this definition; it has hands that move in regular cycles of motion and we do indeed measure elapsed time by counting the number of cycles (or fractions thereof) that the hands swing through between chosen events.
Of course, the meaning of "perfectly regular cycles of motion" implicitly involves a notion of time, since "regular" refers to equal time durations elapsing for each cycle. From a practical standpoint we address this by building clocks out of simple physical components that, on fundamental grounds, we expect to undergo repetitive cyclical evolutions that do not change in any manner from one cycle to the next. Grandfather clocks with pendulums that swing back and forth and atomic clocks based on repetitive atomic processes provide simple examples.
Our goal is to understand how motion affects the passage of time, and since we have defined time operationally in terms of clocks, we can translate our question into how motion affects the "ticking" of clocks. It is crucial to emphasize at the outset that our discussion is not concerned with how the mechanical elements of a particular clock happen to respond to shaking or jostling that might result from bumpy motion. In fact, we will consider only the simplest and most serene kind of motion—motion at absolutely constant velocity—and therefore there will not be any shaking or jostling at all. Rather, we are interested in the universal question of how motion affects the passage of time and therefore how it fundamentally affects the ticking of any and all clocks regardless of their particular design or construction.
For this purpose we introduce the world's conceptually simplest (yet most impractical) clock. It is known as a "light clock" and consists of two small mirrors mounted on a bracket facing one another, with a single photon of light bouncing back and forth between them (see Figure 2.1). If the mirrors are about six inches apart, it will take the photon about a billionth of a second to complete one round-trip journey. "Ticks" on the light clock may be thought of as occurring every time the photon completes a round-trip—a billion ticks means that one second has elapsed.
We can use the light clock like a stopwatch to measure the time elapsed between events: We simply count how many ticks occur during the period of interest and multiply by the time corresponding to one tick. For instance, if we are timing a horse race and count that between the start and finish the number of round-trip photon journeys is 55 billion, we can conclude that the race took 55 seconds.
The reason we use the light clock in our discussion is that its mechanical simplicity pares away extraneous details and therefore provides us with the clearest insight into how motion affects the passage of time. To see this, imagine that we are idly watching the passage of time by looking at a ticking light clock placed on a nearby table. Then, all of sudden, a second light clock slides by on the table, moving at constant velocity (see Figure 2.2) The question we ask is whether the moving light clock will tick at the same rate as the stationary light clock?

Figure 2.1 A light clock consists of two parallel mirrors with a photon that bounces between them. The clock "ticks" each time the photon completes a round-trip journey.

Figure 2.2 A stationary light clock in the foreground while a second light clock slides by at constant speed.
To answer the question, let's consider the path, from our perspective, that the photon in the sliding clock must take in order for it to result in a tick. The photon starts at the base of the sliding clock, as in Figure 2.2, and first travels to the upper mirror. Since, from our perspective, the clock is moving, the photon must travel at an angle, as shown in Figure 2.3. If the photon did not travel along this path, it would miss the upper mirror and fly off into space. As the sliding clock has every right to claim that it's stationary and everything else is moving, we know that the photon will hit the upper mirror and hence the path we have drawn is correct. The photon bounces off the upper mirror and again travels a diagonal path to hit the lower mirror, and the sliding clock ticks. The simple but essential point is that the double diagonal path that we see the photon traverse is longer than the straight up-and-down path taken by the photon in the stationary clock; in addition to traversing the up-and-down distance, the photon in the sliding clock must also travel to the right, from our perspective. Moreover, the constancy of the speed of light tells us that the sliding clock's photon travels at exactly the same speed as the stationary clock's photon. But since it must travel farther to achieve one tick it will tick less frequently. This simple argument establishes that the moving light clock, from our perspective, ticks more slowly than the stationary light clock. And since we have agreed that the number of ticks directly reflects how much time has passed, we see that the passage of time has slowed down for the moving clock.

Figure 2.3 From our perspective, the photon in the sliding clock travels on a diagonal path.
You might wonder whether this merely reflects some special feature of light clocks and would not apply to grandfather clocks or Rolex watches. Would time as measured by these more familiar clocks also slow down? The answer is a resounding yes, as can be seen by an application of the principle of relativity. Let's attach a Rolex watch to the top of each of our light clocks, and rerun the preceding experiment. As discussed, a stationary light clock and its attached Rolex measure identical time durations, with a billion ticks on the light clock occurring for every one second of elapsed time on the Rolex. But what about the moving light clock and its attached Rolex? Does the rate of ticking on the moving Rolex slow down so that it stays synchronized with the light clock to which it is attached? Well, to make the point most forcefully, imagine that the light clock-Rolex watch combination is moving because it is bolted to the floor of a windowless train compartment gliding along perfectly straight and smooth tracks at constant speed. By the principle of relativity, there is no way for an observer on this train to detect any influence of the train's motion. But if the light clock and Rolex were to fall out of synchronization, this would be a noticeable influence indeed. And so the moving light clock and its attached Rolex must still measure equal time durations; the Rolex must slow down in exactly the same way that the light clock does. Regardless of brand, type, or construction, clocks that are moving relative to one another record the passage of time at different rates.
The light clock discussion also makes clear that the precise time difference between stationary and moving clocks depends on how much farther the sliding clock's photon must travel to complete each round-trip journey. This in turn depends on how quickly the sliding clock is moving—from the viewpoint of a stationary observer, the faster the clock is sliding, the farther the photon must travel to the right. We conclude that in comparison to a stationary clock, the rate of ticking of the sliding clock becomes slower and slower as it moves faster and faster.3
To get a sense of scale, note that the photon traverses one round-trip in about a billionth of a second. For the clock to be able to travel an appreciable distance during the time for one tick it must therefore be traveling enormously quickly—that is, some significant fraction of the speed of light. If it is traveling at more commonplace speeds like 10 miles per hour, the distance it can move to the right before one tick is completed is minuscule—just about 15 billionths of a foot. The extra distance that the sliding photon must travel is tiny and it has a correspondingly tiny effect on the rate of ticking of the moving clock. And again, by the principle of relativity, this is true for all clocks—that is, for time itself. This is why beings such as ourselves who travel relative to one another at such slow speeds are generally unaware of the distortions in the passage of time. The effects, although present to be sure, are incredibly small. If, on the other hand, we were able to grab hold of the sliding clock and move with it at, say, three-quarters the speed of light, the equations of special relativity can be used to show that stationary observers would see our moving clock ticking at just about two-thirds the rate of their own. A significant effect, indeed.
Life on the Run
We have seen that the constancy of the speed of light implies that a moving light clock ticks more slowly than a stationary light clock. And by the principle of relativity, this must be true not only for light clocks but also for any clock—it must be true of time itself. Time elapses more slowly for an individual in motion than it does for a stationary individual. If the fairly simple reasoning that has led us to this conclusion is correct, then, for instance, shouldn't one be able to live longer by being in motion rather than staying stationary? After all, if time elapses more slowly for an individual in motion than for an individual at rest, then this disparity should apply not just to time as measured by watches but also to time as measured by heartbeats and the decay of body parts. This is the case, as has been directly confirmed—not with the life expectancy of humans, but with certain particles from the microworld: muons. There is one important catch, however, that prevents us from proclaiming a newfound fountain of youth.
When sitting at rest in the laboratory, muons disintegrate by a process closely akin to radioactive decay, in an average of about two millionths of a second. This disintegration is an experimental fact supported by an enormous amount of evidence. It's as if a muon lives its life with a gun to its head; when it reaches two millionths of a second in age, it pulls the trigger and explodes apart into electrons and neutrinos. But if these muons are not sitting at rest in the laboratory and instead are traveling through a piece of equipment known as a particle accelerator that boosts them to just shy of light-speed, their average life expectancy as measured by scientists in the laboratory increases dramatically. This really happens. At 667 million miles per hour (about 99.5 percent of light speed), the muon lifetime is seen to increase by a factor of about ten. The explanation, according to special relativity, is that "wristwatches" worn by the muons tick much more slowly than the clocks in the laboratory, so long after the laboratory clocks say that the muons should have pulled their triggers and exploded, the watches on the fast-moving muons have yet to reach doom time. This is a very direct and dramatic demonstration of the effect of motion on the passage of time. If people were to zip around as quickly as these muons, their life expectancy would also increase by the same factor. Rather than living seventy years, people would live 700 years.4
Now for the catch. Although laboratory observers see fast-moving muons living far longer than their stationary brethren, this is due to time elapsing more slowly for the muons in motion. This slowing of time applies not just to the watches worn by the muons but also to all activities they might undertake. For instance, if a stationary muon can read 100 books in its short lifetime, its fast-moving cousin will also be able to read the same 100 books, because although it appears to live longer than the stationary muon, its rate of reading—as well as everything else in its life—has slowed down as well. From the laboratory perspective, it's as if the moving muon is living its life in slow motion; from this viewpoint the moving muon will live longer than a stationary one, but the "amount of life" the muon will experience is precisely the same. The same conclusion, of course, holds true for the fast-moving people with a life expectancy of centuries. From their perspective, it's life as usual. From our perspective they are living life in hyper-slow motion and therefore one of their normal life cycles takes an enormous amount of our time.
Who Is Moving, Anyway?
The relativity of motion is both the key to understanding Einstein's theory and a potential source of confusion. You may have noticed that a reversal of perspective interchanges the roles of the "moving" muons, whose watches we have argued run slowly, and their "stationary" counterparts. Just as both George and Gracie had an equal right to declare that they were stationary and that the other was moving, the muons we have described as being in motion are fully justified in proclaiming that, from their perspective, they are motionless and that it is the "stationary" muons that are moving, in the opposite direction. The arguments presented can be applied equally well from this perspective, leading to the seemingly opposite conclusion that watches worn by the muons we christened as stationary are running slow compared with those worn by the muons we described as moving.
We have already met a situation, the signing ceremony with the light bulb, in which different viewpoints lead to results that seem to be completely at odds. In that case we were forced by the basic reasoning of special relativity to give up the ingrained idea that everyone, regardless of state of motion, agrees about which events happen at the same time. The present incongruity, though, appears to be worse. How can two observers each claim that the other's watch is running slower? More dramatically, the different but equally valid muon perspectives seem to lead us to the conclusion that each group will claim, firmly but sadly, that they will die first. We are learning that the world can have some unexpectedly strange features, but we would hope that it does not cross into the realm of logical absurdity. So what's going on?
As with all apparent paradoxes arising from special relativity, under close examination these logical dilemmas resolve to reveal new insights into the workings of the universe. To avoid ever more severe anthropomorphizing, let's switch from muons back to George and Gracie, who now, in addition to their flashing lights, have bright digital clocks on their spacesuits. From George's perspective, he is stationary while Gracie with her flashing green light and large digital clock appears in the distance and then passes him in the blackness of empty space. He notices that Gracie's clock is running slow in comparison to his (with the rate of slowdown depending on how fast they pass one another). Were he a bit more astute, he would also note that in addition to the passage of time on her clock, everything about Gracie—the way she waves as she passes, the speed with which she blinks her eyes, and so on—is occurring in slow motion. From Gracie's perspective, exactly the same observations apply to George.
Although this seems paradoxical, let's try to pinpoint a precise experiment that would reveal a logical absurdity. The simplest possibility is to arrange things so that when George and Gracie pass one another they both set their clocks to read 12:00. As they travel apart, each claims that the other's clock is running slower. To confront this disagreement head on, George and Gracie must rejoin each other and directly compare the time elapsed on their clocks. But how can they do this? Well, George has a jet-pack that he can use, from his perspective, to catch up with Gracie. But if he does this, the symmetry of their two perspectives, which is the cause of the apparent paradox, is broken since George will have undergone accelerated, non-force-free motion. When they rejoin in this manner, less time will indeed have elapsed on George's clock as he can now definitively say that he was in motion, since he could feel it. No longer are George's and Gracie's perspectives on equal footing. By turning on the jet-pack, George relinquishes his claim to being at rest.
If George chases after Gracie in this manner, the time difference that their clocks will show depends on their relative velocity and the details of how George uses his jet-pack. As is by now familiar, if the speeds involved are small, the difference will be minuscule. But if substantial fractions of light speed are involved, the differences can be minutes, days, years, centuries, or more. As one concrete example, imagine that the relative speed of George and Gracie when they pass and are moving apart is 99.5 percent of light speed. Further, let's say that George waits 3 years, according to his clock, before firing up his jet-pack for a momentary blast that sends him closing in on Gracie at the same speed that they were previously moving apart, 99.5 percent of light speed. When he reaches Gracie, 6 years will have elapsed on his clock since it will take him 3 years to catch her. However, the mathematics of special relativity shows that 60 years will have elapsed on her clock. This is no sleight of hand: Gracie will have to search her distant memory, some 60 years before, to recall passing George in space. For George, on the other hand, it was a mere 6 years ago. In a real sense, George's motion has made him a time traveler, albeit in a very precise sense: He has traveled into Gracie's future.
Getting the two clocks back together for direct comparison might seem to be merely a logistical nuisance, but it is really at the heart of the matter. We can imagine a variety of tricks to circumvent this chink in the paradox armor, but all ultimately fail. For instance, rather than bringing the clocks back together, what if George and Gracie compare their clocks by cellular telephone communication? If such communication were instantaneous, we would be faced with an insurmountable inconsistency: reasoning from Gracie's perspective, George's clock is running slow and hence he must communicate less elapsed time; reasoning from George's perspective, Gracie's clock is running slow and hence she must communicate less elapsed time. They both can't be right, and we would be sunk. The key point of course is that cell phones, like all forms of communication, do not transmit their signals instantaneously. Cell phones operate with radio waves, a form of light, and the signal they transmit therefore travels at light speed. This means that it takes time for the signals to be received—just enough time delay, in fact, to make each perspective compatible with the other.
Let's see this, first, from George's perspective. Imagine that every hour, on the hour, George recites into his cell phone, "It's twelve o'clock and all is well," "It's one o'clock and all is well," and so forth. Since from his perspective Gracie's clock runs slow, at first blush he thinks that Gracie will receive these messages prior to her clock's reaching the appointed hour. In this way, he concludes, Gracie will have to agree that hers is the slow clock. But then he rethinks it: "Since Gracie is receding from me, the signal I send to her by cell phone must travel ever longer distances to reach her. Maybe this additional travel time compensates for the slowness of her clock." George's realization that there are competing effects—the slowness of Gracie's clock vs. the travel time of his signal—inspires him to sit down and quantitatively work out their combined effect. The result he finds is that the travel time effect more than compensates for the slowness of Gracie's clock. He comes to the surprising conclusion that Gracie will receive his signals proclaiming the passing of an hour on his clock after the appointed hour has passed on hers. In fact, since George is aware of Gracie's expertise in physics, he knows that she will take the signal's travel time into account when drawing conclusions about his clock based on his cell phone communications. A little more calculation quantitatively shows that even taking the travel time into account, Gracie's analysis of his signals will lead her to the conclusion that George's clock ticks more slowly than hers.
Exactly the same reasoning applies when we take Gracie's perspective, with her sending out hourly signals to George. At first the slowness of George's clock from her perspective leads her to think that he will receive her hourly messages prior to broadcasting his own. But when she takes into account the ever longer distances her signal must travel to catch George as he recedes into the darkness, she realizes that George will actually receive them after sending out his own. Once again, she realizes that even if George takes the travel time into account, he will conclude from Gracie's cell phone communications that her clock is running slower than his.
So long as neither George nor Gracie accelerates, their perspectives are on precisely equal footing. Even though it seems paradoxical, in this way they both realize that it is perfectly consistent for each to think the other's clock is running slow.
Motion's Effect on Space
The preceding discussion reveals that observers see moving clocks ticking more slowly than their own—that is, time is affected by motion. It is a short step to see that motion has an equally dramatic effect on space. Let's return to Slim and Jim on the drag strip. While in the showroom, as we mentioned, Slim had carefully measured the length of his new car with a tape measure. As Slim is speeding along the drag strip, Jim cannot apply this method to measure the length of the car, so he must proceed in an indirect manner. One such approach, as we indicated earlier, is this: Jim starts his stopwatch just when the front bumper of the car reaches him and stops it just as the rear bumper passes. By multiplying the elapsed time by the speed of the car, Jim can determine the car's length.
Using our newfound appreciation of the subtleties of time, we realize that from Slim's perspective he is stationary while Jim is moving, and hence Slim sees Jim's clock as running slow. As a result, Slim realizes that Jim's indirect measurement of the car's length will yield a shorter result than he measured in the showroom, since in Jim's calculation (length equals speed multiplied by elapsed time) Jim measures the elapsed time on a watch that is running slow. If it runs slow, the elapsed time he finds will be less and the result of his calculation will be a shorter length.
Thus Jim will perceive the length of Slim's car, when it is in motion, to be less than its length when measured at rest. This is an example of the general phenomenon that observers perceive a moving object as being shortened along the direction of its motion. For instance, the equations of special relativity show that if an object is moving at about 98 percent of light speed, then a stationary observer will view it as being 80 percent shorter than if it were at rest. This phenomenon is illustrated in Figure 2.4.5
Motion through Spacetime
The constancy of the speed of light has resulted in a replacement of the traditional view of space and time as rigid and objective structures with a new conception in which they depend intimately on the relative motion between observer and observed. We could end our discussion here, having realized that moving objects evolve in slow motion and are foreshortened. Special relativity, though, provides a more deeply unified perspective to encompass these phenomena.
To understand this perspective, let's imagine a rather impractical automobile that rapidly attains its cruising speed of 100 miles per hour and sticks to this speed, no more, no less, until it is shut off and rolls to a halt. Let's also imagine that, due to his growing reputation as a skilled driver, Slim is asked to test-drive the vehicle on a long, straight, and wide track in the middle of a flat stretch of desert. As the distance between the start and finish lines is 10 miles, the car should cover this distance in one-tenth of an hour, or six minutes. Jim, who moonlights as an automobile engineer, inspects the data recorded from dozens of test-drives and is disturbed to see that although most were timed to be six minutes, the last few are a good deal longer: 6.5, 7, and even 7.5 minutes. At first he suspects a mechanical problem, since those times seem to indicate that the car was traveling slower than 100 miles per hour on the last three runs. Yet after examining the car extensively he convinces himself that it is in perfect condition. Unable to explain the anomalously long times, he consults Slim and asks him about the final few runs. Slim has a simple explanation. He tells Jim that, since the track runs from east to west, as it got later in the day, the sun was glaring into his view. During the last three runs it was so bad that he drove from one end of the track to the other at a slight angle. He draws a rough sketch of the path he took on the last three runs, and it is shown in Figure 2.5. The explanation for the three longer times is now perfectly clear: the path from start to finish is longer when traveling at an angle and therefore, at the same speed of 100 miles per hour, it will take more time to cover. Put another way, when traveling at an angle, part of the 100 miles per hour is expended on going from south to north, leaving a bit less to accomplish the trip from east to west. This implies that it will take a little longer to traverse the strip.

Figure 2.4 A moving object is shortened in the direction of its motion.
As stated, Slim's explanation is easy to understand; however, it is worth rephrasing it slightly for the conceptual leap we are about to take. The north-south and east-west directions are two independent spatial dimensions in which a car can move. (It can also move vertically, when traversing a mountain pass, for example, but we will not need that ability here.) Slim's explanation illustrates that even though the car was traveling at 100 miles per hour on each and every run, during the last few runs it shared this speed between the two dimensions and hence appeared to be going slower than 100 miles per hour in the east-west direction. During the previous runs, all 100 miles per hour were devoted to purely east-west motion; during the last three, part of this speed was used for north-south motion as well.
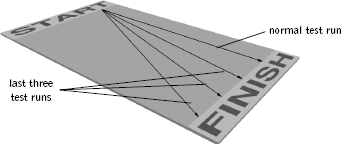
Figure 2.5 Due to the glaring late-afternoon sun, Slim drove at an increasingly greater angle on the last three runs.
Einstein found that precisely this idea—the sharing of motion between different dimensions—underlies all of the remarkable physics of special relativity, so long as we realize that not only can spatial dimensions share an object's motion, but the time dimension can share this motion as well. In fact, in the majority of circumstances, most of an object's motion is through time, not space. Let's see what this means.
Motion through space is a concept we learn about early in life. Although we often don't think of things in such terms, we also learn that we, our friends, our belongings, and so forth all move through time, as well. When we look at a clock or a wristwatch, even while we idly sit and watch TV, the reading on the watch is constantly changing, constantly "moving forward in time." We and everything around us are aging, inevitably passing from one moment in time to the next. In fact, the mathematician Hermann Minkowski, and ultimately Einstein as well, advocated thinking about time as another dimension of the universe—the fourth dimension—in some ways quite similar to the three spatial dimensions in which we find ourselves immersed. Although it sounds abstract, the notion of time as a dimension is actually concrete. When we want to meet someone, we tell them where "in space" we will expect to see them—for instance, the 9th floor of the building on the corner of 53rd Street and 7th Avenue. There are three pieces of information here (9th floor, 53rd Street, 7th Avenue) reflecting a particular location in the three spatial dimensions of the universe. Equally important, however, is our specification of when we expect to meet them—for instance, at 3 P.M. This piece of information tells us where "in time" our meeting will take place. Events are therefore specified by four pieces of information: three in space and one in time. Such data, it is said, specifies the location of the event in space and in time, or in spacetime, for short. In this sense, time is another dimension.
Since this view proclaims that space and time are simply different examples of dimensions, can we speak of an object's speed through time in a manner resembling the concept of its speed through space? We can.
A big clue for how to do this comes from a central piece of information we have already encountered. When an object moves through space relative to us, its clock runs slow compared to ours. That is, the speed of its motion through time slows down. Here's the leap: Einstein proclaimed that all objects in the universe are always traveling through spacetime at one fixed speed—that of light. This is a strange idea; we are used to the notion that objects travel at speeds considerably less than that of light. We have repeatedly emphasized this as the reason relativistic effects are so unfamiliar in the everyday world. All of this is true. We are presently talking about an object's combined speed through all four dimensions—three space and one time—and it is the object's speed in this generalized sense that is equal to that of light. To understand this more fully and to reveal its importance, we note that like the impractical single-speed car discussed above, this one fixed speed can be shared between the different dimensions—different space andtime dimensions, that is. If an object is sitting still (relative to us) and consequently does not move through space at all, then in analogy to the first runs of the car, all of the object's motion is used to travel through one dimension—in this case, the time dimension. Moreover, all objects that are at rest relative to us and to each other move through time—they age—at exactly the same rate or speed. If an object does move through space, however, this means that some of the previous motion through time must be diverted. Like the car traveling at an angle, this sharing of motion implies that the object will travel more slowly through time than its stationary counterparts, since some of its motion is now being used to move through space. That is, its clock will tick more slowly if it moves through space. This is exactly what we found earlier. We now see that time slows down when an object moves relative to us because this diverts some of its motion through time into motion through space. The speed of an object through space is thus merely a reflection of how much of its motion through time is diverted.6
We also see that this framework immediately incorporates the fact that there is a limit to an object's spatial velocity: the maximum speed through space occurs if all of an object's motion through time is diverted to motion through space. This occurs when all of its previous light-speed motion through time is diverted to light-speed motion through space. But having used up all of its motion through time, this is the fastest speed through space that the object—any object—can possibly achieve. This is analogous to our car being test-driven directly in the north-south direction. Just as the car will have no speed left for motion in the east-west dimension, something traveling at light speed through space will have no speed left for motion through time. Thus light does not get old; a photon that emerged from the big bang is the same age today as it was then. There is no passage of time at light speed.
What about E=mc2?
Although Einstein did not advocate calling his theory "relativity" (suggesting instead the name "invariance" theory to reflect the unchanging character of the speed of light, among other things), the meaning of the term is now clear. Einstein's work showed that concepts such as space and time, which had previously seemed to be separate and absolute, are actually interwoven and relative. Einstein went on to show that other physical properties of the world are unexpectedly interwoven as well. His most famous equation provides one of the most important examples. In it, Einstein asserted that the energy (E) of an object and its mass (m) are not independent concepts; we can determine the energy from knowledge of the mass (by multiplying the latter twice by the speed of light, c2) or we can determine the mass from knowledge of the energy (by dividing the latter twice by the speed of light). In other words, energy and mass—like dollars and francs—are convertible currencies. Unlike money, however, the exchange rate given by two factors of the speed of light is always and forever fixed. Since this exchange-rate factor is so large (c2 is a big number), a little mass goes an extremely long way in producing energy. The world grasped the devastating destructive power arising from the conversion of less than 1 percent of two pounds of uranium into energy at Hiroshima; one day, through fusion power plants, we may productively use Einstein's formula to meet the energy demands of the whole world with our endless supply of seawater.
From the viewpoint of the concepts we have emphasized in this chapter, Einstein's equation gives us the most concrete explanation for the central fact that nothing can travel faster than light speed. You may have wondered, for instance, why we can't take some object, a muon say, that an accelerator has boosted up to 667 million miles per hour—99.5 percent of light speed—and "push it a bit harder," getting it to 99.9 percent of light speed, and then "really push it harder" impelling it to cross the light-speed barrier. Einstein's formula explains why such efforts will never succeed. The faster something moves the more energy it has and from Einstein's formula we see that the more energy something has the more massive it becomes. Muons traveling at 99.9 percent of light speed, for example, weigh a lot more than their stationary cousins. In fact, they are about 22 times as heavy—literally. (The masses recorded in Table 1.1 are for particles at rest.) But the more massive an object is, the harder it is to increase its speed. Pushing a child on a bicycle is one thing, pushing a Mack truck is quite another. So, as a muon moves more quickly it gets ever more difficult to further increase its speed. At 99.999 percent of light speed the mass of a muon has increased by a factor of 224; at 99.99999999 percent of light speed it has increased by a factor of more than 70,000. Since the mass of the muon increases without limit as its speed approaches that of light, it would require a push with an infinite amount of energy to reach or to cross the light barrier. This, of course, is impossible and hence absolutely nothing can travel faster than the speed of light.
As we shall see in the next chapter, this conclusion plants the seeds for the second major conflict faced by physics during the past century and ultimately spells doom for another venerable and cherished theory—Newton's universal theory of gravity.