The Elegant Universe: Superstrings, Hidden Dimensions, and the Quest for the Ultimate Theory - Brian Greene (2010)
Notes
Chapter 1
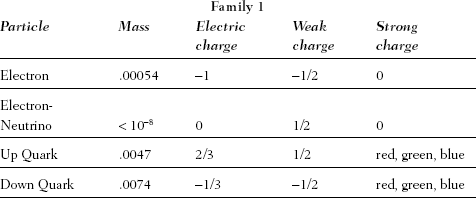
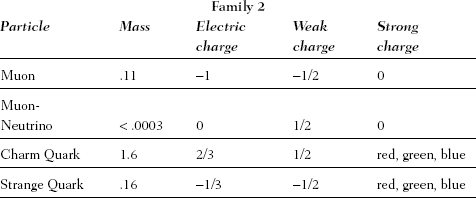
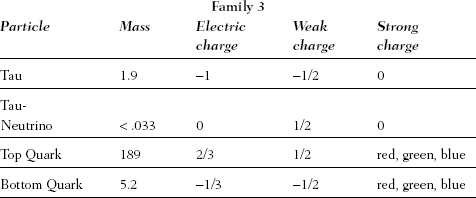
1. The table below is an elaboration of Table 1.1. It records the masses and force charges of the particles of all three families. Each type of quark can carry three possible strong-force charges that are, somewhat fancifully, labeled as colors—they stand for numerical strong-force charges values. The weak charges recorded are, more precisely, the "third-component" of weak isospin. (We have not listed the "right-handed" components of the particles—they differ by having no weak charge.)
2. Strings can also have two freely moving ends (so-called open strings) in addition to the loops (closed strings) illustrated in Figure 1.1. To ease our presentation, for the most part we will focus on closed strings, although essentially all of what we say applies to both.
3. Albert Einstein, in a 1942 letter to a friend, as quoted in Tony Hey and Patrick Walters, Einstein's Mirror (Cambridge, Eng.: Cambridge University Press, 1997).
4. Steven Weinberg, Dreams of a Final Theory (New York: Pantheon, 1992), p.52.
5. Interview with Edward Witten, May 11, 1998.
Chapter 2
1. The presence of massive bodies like the earth does complicate matters by introducing gravitational forces. Since we are now focusing on motion in the horizontal direction—not the vertical direction—we can and will ignore the earth's presence. In the next chapter we will undertake a thorough discussion of gravity.
2. More precisely, the speed of light through the vacuum of empty space is 670 million miles per hour. When light travels through a substance such as air or glass its speed is decreased in roughly the same way that a rock dropped from a cliff is dragged to a slower speed when it enters a body of water. This slowing of light relative to its speed through a vacuum is of no consequence for our discussion of relativity and is justifiably ignored throughout the text.
3. For the mathematically inclined reader, we note that these observations can be turned into quantitative statements. For instance, if the moving light clock has speed v and it takes t seconds for its photon to complete one round-trip journey (as measured by our stationary light clock), then the light clock will have traveled a distance vt when its photon has returned to the lower mirror. We can now use the Pythagorean theorem to calculate that the length of each of the diagonal paths in Figure 2.3 is 
(vt/2)2 + h2, where h is the distance between the two mirrors of a light clock (taken to be six inches in the text). The two diagonal paths, taken together, therefore have length 2(vt/2)2 + h2 . Since the speed of light has a constant value, conventionally called c, it takes light 2(vt/2)2 + h2/c seconds to complete the double diagonal journey. And so, we have the equality t = 2(vt/2)2 + h2/c, which can be solved for t, yielding t = 2h/c2-v2. To avoid confusion, let's write this as tmoving = 2h/c2-v2, where the subscript indicates that this is the time we measure for one tick to occur on the moving clock. On the other hand, the time for one tick on our stationary clock is tstationary = 2h/c and as a little algebra reveals, tmoving = tstationary/1-v2/c2, directly showing that one tick on the moving clock takes longer than one tick on the stationary clock. This means that between chosen events, fewer total ticks will take place on the moving clock than on the stationary, ensuring that less time has elapsed for the observer in motion.
4. In case you would be more convinced by an experiment carried out in a less esoteric setting than a particle accelerator, consider the following. During October 1971, J. C. Hafele, then of Washington University in St. Louis, and Richard Keating of the United States Naval Observatory flew cesium-beam atomic clocks on commercial airliners for some 40 hours. After taking into account a number of subtle features having to do with gravitational effects (to be discussed in the next chapter), special relativity claims that the total elapsed time on the moving atomic clocks should be less than the elapsed time on stationary earthbound counterparts by a few hundred billionths of a second. This is just what Hafele and Keating found: Time really does slow down for a clock in motion.
5. Although Figure 2.4 correctly illustrates the shrinking of an object along its direction of motion, the image does not illustrate what we would actually see if an object were somehow to blaze by at nearly light speed (assuming our eyesight or photographic equipment were sharp enough to see anything at all!). To see something, our eyes—or our camera—must receive light that has reflected off the object's surface. But since the reflected light travels to us from various locations on the object, the light we see at any moment traveled to us along paths of different lengths. This results in a kind of relativistic visual illusion in which the object will appear both foreshortened and rotated.
6. For the mathematically inclined reader, we note that from the spacetime position 4-vector x = (ct, x1, x2, x3) = (ct, 
) we can produce the velocity 4-vector u = dx/dt, where t is the proper time defined by dt2 = dt2-c-2(dx21 + dx22 + dx23). Then, the "speed through spacetime" is the magnitude of the 4-vector u, ((c2dt2-dx2)/(dt2-c-2dx2)), which is identically the speed of light, c. Now, we can rearrange the equation c2(dt/dt)2-(d/d
)2 = c2, to be c2(d/dt)2 + (d/dt)2 = c2. This shows that an increase in an object's speed through space, (d/dt)2 must be accompanied by a decrease in dt/dt, the latter being the object's speed through time (the rate at which time elapses on its own clock, dt, as compared with that on our stationary clock, dt).
Chapter 3
1. Isaac Newton, Sir Isaac Newton's Mathematical Principle of Natural Philosophy and His System of the World, trans. A. Motte and Florian Cajori (Berkeley: University of California Press, 1962), Vol. I, p. 634.
2. A bit more precisely, Einstein realized that the equivalence principle holds so long as your observations are confined to a small enough region of space—that is, so long as your "compartment" is small enough. The reason is the following. Gravitational fields can vary in strength (and in direction) from place to place. But we are imagining that your whole compartment accelerates as a single unit and therefore your acceleration simulates a single, uniform gravitational force field. As your compartment gets ever smaller, though, there is ever less room over which a gravitational field can vary, and hence the equivalence principle becomes ever more applicable. Technically, the difference between the uniform gravitational field simulated by an accelerated vantage point and a possibly nonuniform "real" gravitational field created by some collection of massive bodies is known as the "tidal" gravitational field (since it accounts for the moon's gravitational effect on tides on earth). This endnote, therefore, can be summarized by saying that tidal gravitational fields become less noticeable as the size of your compartment gets smaller, making accelerated motion and a "real" gravitational field indistinguishable.
3. Albert Einstein, as quoted in Albrecht Fölsing, Albert Einstein (New York: Viking, 1997), p. 315.
4. John Stachel, "Einstein and the Rigidly Rotating Disk," in General Relativity and Gravitation, ed. A. Held (New York: Plenum, 1980), p. 1.
5. Analysis of the Tornado ride, or the "rigidly rotating disk," as it is called in more technical language, easily leads to confusion. In fact, to this day there is not universal agreement on a number of subtle aspects of this example. In the text we have followed the spirit of Einstein's own analysis, and in this endnote we continue to take this viewpoint and seek to clarify a couple of features that you may have found confusing. First, you may be puzzled about why the circumference of the ride is not Lorentz contracted in exactly the same way as the ruler, and hence measured by Slim to have the same length as we originally found. Bear in mind, though, that throughout our discussion the ride was always spinning; we never analyzed the ride when it was at rest. Thus, from our perspective as stationary observers, the only difference between our and Slim's measurement of the ride's circumference is that Slim's ruler is Lorentz contracted; the spinning Tornado ride was spinning when we performed our measurement, and it is spinning as we watch Slim carry out his. Since we see that his ruler is contracted, we realize that he will have to lay it out more times to traverse the entire circumference, thereby measuring a longer length than we did. Lorentz contraction of the ride's circumference would have been relevant only if we compared the properties of the ride when spinning and when at rest, but this is a comparison we did not need.
Second, notwithstanding the fact that we did not need to analyze the ride when it was at rest, you may still be wondering about what would happen when it does slow down and stop. Now, it would seem, we must take account of the changing circumference with changing speed due to different degrees of Lorentz contraction. But how can this be squared with an unchanging radius? This is a subtle problem whose resolution hinges on the fact that there are no fully rigid objects in the real world. Objects can stretch and bend and thereby accommodate the stretching or contracting we have come upon; if not, as Einstein pointed out, a rotating disk that was initially formed by allowing a spinning cast of molten metal to cool while in motion would break apart if its rate of spinning were subsequently changed. For more details on the history of the rigidly rotating disk, see Stachel, "Einstein and the Rigidly Rotating Disk."
6. The expert reader will recognize that in the example of the Tornado ride, that is, in the case of a uniformly rotating frame of reference, the curved three-dimensional spatial sections on which we have focused fit together into a four-dimensional spacetime whose curvature still vanishes.
7. Hermann Minkowski, as quoted in Fölsing, Albert Einstein, p. 189.
8. Interview with John Wheeler, January 27, 1998.
9. Even so, existing atomic clocks are sufficiently accurate to detect such tiny—and even tinier—time warps. For instance, in 1976 Robert Vessot and Martin Levine of the Harvard-Smithsonian Astrophysical Observatory, together with collaboraters at the National Aeronautics and Space Administration (NASA), launched a Scout D rocket from Wallops Island, Virginia, that carried an atomic clock accurate to about a trillionth of a second per hour. They hoped to show that as the rocket gained altitude (thereby decreasing the effect of the earth's gravitational pull), an identical earthbound atomic clock (still subject to the full force of the earth's gravity) would tick more slowly. Through a two-way stream of microwave signals, the researchers were able to compare the rate of ticking of the two atomic clocks and, indeed, at the rocket's maximum altitude of 6,000 miles, its atomic clock ran fast by about 4 parts per billion relative to its counterpart on earth, agreeing with theoretical predictions to better than a hundredth of a percent.
10. In the mid-1800s, the French scientist Urbain Jean Joseph Le Verrier discovered that the planet Mercury deviates slightly from the orbit around the sun that is predicted by Newton's law of gravity. For more than half a century, explanations for this so-called excess orbital perihelion precession (in plain language, at the end of each orbit, Mercury does not quite wind up where Newton's theory says it should) ran the gamut—the gravitational influence of an undiscovered planet or planetary ring, an undiscovered moon, the effect of interplanetary dust, the oblateness of the sun—but none was sufficiently compelling to win general acceptance. In 1915, Einstein calculated the perihelion precession of Mercury using his newfound equations of general relativity and found an answer that, by his own admission, gave him heart palpitations: The result from general relativity precisely matched observations. This success, certainly, was one significant reason that Einstein had such faith in his theory, but most everyone else awaited confirmation of a prediction, rather than an explanation of a previously known anomaly. For more details, see Abraham Pais, Subtle Is the Lord (New York: Oxford University Press, 1982), p. 253.
11. Robert P. Crease and Charles C. Mann, The Second Creation (New Brunswick, N.J.: Rutgers University Press, 1996), p. 39.
12. Surprisingly, recent research on the detailed rate of cosmic expansion suggests that the universe may in fact incorporate a very small but nonzero cosmological constant.
Chapter 4
1. Richard Feynman, The Character of Physical Law (Cambridge, Mass.: MIT Press, 1965), p. 129.
2. Although Planck's work did solve the infinite energy puzzle, apparently this goal was not what directly motivated his work. Rather, Planck was seeking to understand a closely related issue: the experimental results concerning how energy in a hot oven—a "black body" to be more precise—is distributed over various wavelength ranges. For more details on the history of these developments, the interested reader should consult Thomas S. Kuhn, Black-Body Theory and the Quantum Discontinuity, 1894-1912 (Oxford, Eng.: Clarendon, 1978).
3. A little more precisely, Planck showed that waves whose minimum energy content exceeds their purported average energy contribution (according to nineteenth-century thermodynamics) are exponentially suppressed. This suppression is increasingly sharp as we examine waves of ever larger frequency.
4. Planck's constant is 1.05 × 10-27 grams-centimeters2/second.
5. Timothy Ferris, Coming of Age in the Milky Way (New York: Anchor, 1989), p. 286.
6. Stephen Hawking, lecture at the Amsterdam Symposium on Gravity, Black Holes, and String Theory, June 21, 1997.
7. It is worthwhile to note that Feynman's approach to quantum mechanics can be used to derive the approach based on wave functions, and vice versa; the two approaches, therefore, are fully equivalent. Nevertheless, the concepts, the language, and the interpretation that each approach emphasizes are rather different, even though the answers each gives are absolutely identical.
8. Richard Feynman, QED: The Strange Theory of Light and Matter (Princeton: Princeton University Press, 1988).
Chapter 5
1. Stephen Hawking, A Brief History of Time (New York: Bantam Books, 1988), p. 175.
2. Richard Feynman, as quoted in Timothy Ferris, The Whole Shebang (New York: Simon & Schuster, 1997), p. 97.
3. In case you are still perplexed about how anything at all can happen within a region of space that is empty, it is important to realize that the uncertainty principle places a limit on how "empty" a region of space can actually be; it modifies what we mean by empty space. For example, when applied to wave disturbances in a field (such as electromagnetic waves traveling in the electromagnetic field) the uncertainty principle shows that the amplitude of a wave and the speed with which its amplitude changes are subject to the same inverse relationship as are the position and speed of a particle: The more precisely the amplitude is specified the less we can possibly know about the speed with which its amplitude changes. Now, when we say that a region of space is empty, we typically mean that, among other things, there are no waves passing through it, and that all fields have value zero. In clumsy but ultimately useful language, we can rephrase this by saying that the amplitudes of all waves that pass through the region are zero, exactly. But if we know the amplitudes exactly, the uncertainty principle implies that the rate of change of the amplitudes is completely uncertain and can take on essentially any value. But if the amplitudes change, this means that in the next moment they will no longer be zero, even though the region of space is still "empty." Again, on average the field will be zero since at some places its value will be positive while at others negative; on average the net energy in the region has not changed. But this is only on average. Quantum uncertainty implies that the energy in the field—even in an empty region of space—fluctuates up and down, with the size of the fluctuations getting larger as the distance and time scales on which the region is examined get smaller. The energy embodied in such momentary field fluctuations can then, through E = mc2, be converted into the momentary creation of pairs of particles and their antiparticles, which annihilate each other in great haste, to keep the energy from changing, on average.
4. Even though the initial equation that Schrödinger wrote down—the one incorporating special relativity—did not accurately describe the quantum-mechanical properties of electrons in hydrogen atoms, it was soon realized to be a valuable equation when appropriately used in other contexts, and, in fact, is still in use today. However, by the time Schrödinger published his equation he had been scooped by Oskar Klein and Walter Gordon, and hence his relativistic equation is called the "Klein-Gordon equation."
5. For the mathematically inclined reader, we note that the symmetry principles used in elementary particle physics are generally based on groups, most notably, Lie groups. Elementary particles are arranged in representations of various groups and the equations governing their time evolution are required to respect the associated symmetry transformations. For the strong force, this symmetry is called SU(3) (the analog of ordinary three-dimensional rotations, but acting on a complex space), and the three colors of a given quark species transform in a three-dimensional representation. The shifting (from red, green, blue to yellow, indigo, violet) mentioned in the text is, more precisely, an SU(3) transformation acting on the "color coordinates" of a quark. A gauge symmetry is one in which the group transformations can have a spacetime dependence: in this case, "rotating" the quark colors differently at different locations in space and moments in time.
6. During the development of the quantum theories of the three nongravitational forces, physicists also came upon calculations that gave infinite results. In time, though, they gradually realized that these infinities could be done away with through a tool known as renormalization. The infinities arising in attempts to merge general relativity and quantum mechanics are far more severe and are not amenable to the renormalization cure. Even more recently, physicists have realized that infinite answers are a signal that a theory is being used to analyze a realm that is beyond the bounds of its applicability. Since the goal of current research is to find a theory whose range of applicability is, in principle, unbounded—the "ultimate" or "final" theory—physicists want to find a theory in which infinite answers do not crop up, regardless of how extreme the physical system being analyzed might be.
7. The size of the Planck length can be understood based upon simple reasoning rooted in what physicists call dimensional analysis. The idea is this. When a theory is formulated as a collection of equations, the abstract symbols must be tied to physical features of the world if the theory is to make contact with reality. In particular, we must introduce a system of units so that if a symbol, say, is meant to refer to a length, we have a scale by which its value can be interpreted. After all, if equations show that the length in question is 5, we need to know if that means 5 centimeters, 5 kilometers, or 5 light years, etc. In a theory that involves general relativity and quantum mechanics, a choice of units emerges naturally, in the following way. There are two constants of nature upon which general relativity depends: the speed of light, c, and Newton's gravitation constant, G. Quantum mechanics depends on one constant of nature 
. By examining the units of these constants (e.g., c is a velocity, so is expressed as distance divided by time, etc.), one can see that the combination G/c3 has the units of a length; in fact, it is 1.616 × 10-33 centimeters. This is the Planck length. Since it involves gravitational and spacetime inputs (G and c) and has a quantum mechanical dependence () as well, it sets the scale for measurements—the natural unit of length—in any theory that attempts to merge general relativity and quantum mechanics. When we use the term "Planck length" in the text, it is often meant in an approximate sense, indicating a length that is within a few orders of magnitude of 10-33 centimeters.
8. Currently, in addition to string theory, two other approaches for merging general relativity and quantum mechanics are being pursued vigorously. One approach is led by Roger Penrose of Oxford University and is known as twistor theory. The other approach—inspired in part by Penrose's work—is led by Abhay Ashtekar of Pennsylvania State University and is known as the new variables method. Although these other approaches will not be discussed further in this book, there is growing speculation that they may have a deep connection to string theory and that possibly, together with string theory, all three approaches are honing in on the same solution for merging general relativity and quantum mechanics.
Chapter 6
1. The expert reader will recognize that this chapter focuses solely on perturbative string theory; nonperturbative aspects are discussed in Chapters 12 and 13.
2. Interview with John Schwarz, December 23, 1997.
3. Similar suggestions were made independently by Tamiaki Yoneya and by Korkut Bardakci and Martin Halpern. The Swedish physicist Lars Brink also contributed significantly to the early development of string theory.
4. Interview with John Schwarz, December 23, 1997.
5. Interview with Michael Green, December 20, 1997.
6. The standard model does suggest a mechanism by which particles acquire mass—the Higgs mechanism, named after the Scottish physicist Peter Higgs. But from the point of view of explaining the particle masses, this merely shifts the burden to explaining properties of a hypothetical "mass-giving particle"—the so-called Higgs boson. Experimental searches for this particle are underway, but once again, if it is found and its properties measured, these will be input data for the standard model, for which the theory offers no explanation.
7. For the mathematically inclined reader, we note that the association between string vibrational patterns and force charges can be described more precisely as follows. When the motion of a string is quantized, its possible vibrational states are represented by vectors in a Hilbert space, much as for any quantum-mechanical system. These vectors can be labeled by their eigenvalues under a set of commuting hermitian operators. Among these operators are the Hamiltonian, whose eigenvalues give the energy and hence the mass of the vibrational state, as well as operators generating various gauge symmetries that the theory respects. The eigenvalues of these latter operators give the force charges carried by the associated vibrational string state.
8. Based upon insights gleaned from the second superstring revolution (discussed in Chapter 12), Witten and, most notably, Joe Lykken of the Fermi National Accelerator Laboratory have identified a subtle, yet possible, loophole in this conclusion. Lykken, exploiting this realization, has suggested that it might be possible for strings to be under far less tension, and therefore be substantially larger in size, than originally thought. So large, in fact, that they might be observable by the next generation of particle accelerators. If this long-shot possibility turns out to be the case, there is the exciting prospect that many of the remarkable implications of string theory discussed in this and the following chapters will be verifiable experimentally within the next decade. But even in the more "conventional" scenario espoused by string theorists, in which strings are typically on the order of 10-33 centimeters in length, there are indirect ways to search for them experimentally, as we will discuss in Chapter 9.
9. The expert reader will recognize that the photon produced in a collision between an electron and a positron is a virtual photon and therefore must shortly relinquish its energy by dissociating into a particle-antiparticle pair.
10. Of course, a camera works by collecting photons that bounce off the object of interest and recording them on a piece of photographic film. Our use of a camera in this example is symbolic, since we are not imagining bouncing photons off of the colliding strings. Rather, we simply want to record in Figure 6.7(c) the whole history of the interaction. Having said that, we should point out one further subtle point that the discussion in the text glosses over. We learned in Chapter 4 that we can formulate quantum mechanics using Feynman's sum-over-paths method, in which we analyze the motion of objects by combining contributions from all possible trajectories that lead from some chosen starting point to some chosen destination (with each trajectory contributing with a statistical weight determined by Feynman). In Figures 6.6 and 6.7 we show one of the infinite number of possible trajectories followed by point particles (Figure 6.6) or by strings (Figure 6.7) taking them from their initial positions to their final destinations. The discussion in this section, however, applies equally well to any of the other possible trajectories and therefore applies to the whole quantum-mechanical process itself. (Feynman's formulation of point-particle quantum mechanics in the sum-over-paths framework was generalized to string theory through the work of Stanley Mandelstam of the University of California at Berkeley and by the Russian physicist Alexander Polyakov, who is now on the faculty of the physics department of Princeton University.)
Chapter 7
1. Albert Einstein, as quoted in R. Clark, Einstein: The Life and Times (New York: Avon Books, 1984), p. 287.
2. More precisely, spin-1/2 means that the angular momentum of the electron from its spin is /2.
3. The discovery and development of supersymmetry has a complicated history. In addition to those cited in the text, essential early contributions were made by R. Haag, M. Sohnius, J. T. Lopuszanski, Y. A. Gol'fand, E. P. Lichtman, J. L. Gervais, B. Sakita, V. P. Akulov, D. V. Volkov, and V. A. Soroka, among many others. Some of their work is documented in Rosanne Di Stefano, Notes on the Conceptual Development of Supersymmetry, Institute for Theoretical Physics, State University of New York at Stony Brook, preprint ITP-SB-8878.
4. For the mathematically inclined reader we note that this extension involves augmenting the familiar Cartesian coordinates of spacetime with new quantum coordinates, say u and v, that are anticommuting: u × v =-v × u. Supersymmetry can then be thought of as translations in this quantum-mechanically augmented form of spacetime.
5. For the reader interested in more details of this technical issue we note the following. In note 6 of Chapter 6 we mentioned that the standard model invokes a "mass-giving particle"—the Higgs boson—to endow the particles of Tables 1.1 and 1.2 with their observed masses. For this procedure to work, the Higgs particle itself cannot be too heavy; studies show that its mass should certainly be no greater than about 1,000 times the mass of a proton. But it turns out that quantum fluctuations tend to contribute substantially to the mass of the Higgs particle, potentially driving its mass all the way to the Planck scale. Theorists have found, however, that this outcome, which would uncover a major defect in the standard model, can be avoided if certain parameters in the standard model (most notably, the so-called bare mass of the Higgs particle) are finely tuned to better than 1 part in 1015 to cancel the effects of these quantum fluctuations on the Higgs particle's mass.
6. One subtle point to note about Figure 7.1 is that the strength of the weak force is shown to be between that of the strong and electromagnetic forces, whereas we have previously said that it is weaker than both. The reason for this lies in Table 1.2, in which we see that the messenger particles of the weak force are quite massive, whereas those of the strong and electromagnetic forces are massless. Intrinsically, the strength of the weak force (as measured by its coupling constant—an idea we will come upon in Chapter 12) is as shown in Figure 7.1, but its massive messenger particles are sluggish conveyers of its influence and diminish its effects. In Chapter 14 we will see how the gravitational force fits into Figure 7.1.
7. Edward Witten, lecture at the Heinz Pagels Memorial Lecture Series, Aspen, Colorado, 1997.
8. For an in-depth discussion of these and related ideas, see Steven Weinberg, Dreams of a Final Theory.
Chapter 8
1. This is a simple idea, but since the imprecision of common language can sometimes lead to confusion, two clarifying remarks are in order. First, we are assuming that the ant is constrained to live on the surface of the garden hose. If, on the contrary, the ant could burrow into the interior of the hose—if it could penetrate into the rubber material of the hose—we would need three numbers to specify its position, since we would need to also specify how deeply it had burrowed. But if the ant lives only on the hose's surface, its location can be specified with just two numbers. This leads to our second point. Even with the ant living on the hose's surface, we could, if we so chose, specify its location with three numbers: the ordinary left-right, back-forth, and up-down positions in our familiar three-dimensional space. But once we know that the ant lives on the surface of the hose, the two numbers referred to in the text give the minimal data that uniquely specify the ant's position. This is what we mean by saying that the surface of the hose is two-dimensional.
2. Surprisingly, the physicists Savas Dimopoulos, Nima Arkani-Hamed, and Gia Dvali, building on earlier insights of Ignatios Antoniadis and Joseph Lykken, have pointed out that even if an extra curled-up dimension were as large as a millimeter in size, it is possible that it would not yet have been detected experimentally. The reason is that particle accelerators probe the microworld by utilizing the strong, weak, and electromagnetic forces. The gravitational force, being incredibly feeble at technologically accessible energies, is generally ignored. But Dimopoulos and his collaborators note that if the extra curled-up dimension has an impact predominantly on the gravitational force (something, it turns out, that is quite plausible in string theory), all extant experiments could well have overlooked it. New, highly sensitive gravitational experiments will look for such "large" curled-up dimensions in the near future. A positive result would be one of the greatest discoveries of all time.
3. Edwin Abbott, Flatland (Princeton: Princeton University Press, 1991).
4. A. Einstein in letter to T. Kaluza as quoted in Abraham Pais, "Subtle is the Lord": The Science and the Life of Albert Einstein (Oxford: Oxford University Press, 1982), p. 330.
5. A. Einstein in letter to T. Kaluza as quoted in D. Freedman and P. van Nieuwenhuizen, "The Hidden Dimensions of Spacetime," Scientific American 252 (1985), 62.
6. Ibid.
7. Physicists found that the most difficult feature of the standard model to incorporate through a higher-dimensional formulation is something known as chirality. So as not to overburden the discussion we have not covered this concept in the main text, but for readers who are interested we do so briefly here. Imagine that someone shows you a film of some particular scientific experiment and confronts you with the unusual challenge of determining whether the film shot the experiment directly or whether it shot the experiment by looking at its reflection in a mirror. As the cinematographer was quite expert, there are no telltale signs of a mirror being involved. Is this a challenge you can meet? In the mid-1950s, the theoretical insights of T. D. Lee and C. N. Yang, and the experimental results of C. S. Wu and collaborators, showed that you can meet the challenge, so long as an appropriate experiment had been filmed. Namely, their work established that the laws of the universe are not perfectly mirror symmetric in the sense that the mirror-reflected version of certain processes—those directly dependent on the weak force—cannot happen in our world, even though the original process can. And so, as you watch the film if you see one of these forbidden processes occur, you will know that you are watching a mirror-reflected image of the experiment, as opposed to the experiment itself. Since mirrors interchange left and right, the work of Lee, Yang, and Wu established that the universe is not perfectly left-right symmetric—in the language of the field, the universe is chiral. It is this feature of the standard model (the weak force, in particular) that physicists found nearly impossible to incorporate into a higher-dimensional supergravity framework. To avoid confusion, we note that in Chapter 10 we will discuss a concept in string theory known as "mirror symmetry," but the use of the word "mirror" in that context is completely different from its use here.
8. For the mathematically inclined reader, we note that a Calabi-Yau manifold is a complex Kähler manifold with vanishing first Chern class. In 1957 Calabi conjectured that every such manifold admits a Ricci-flat metric, and in 1977 Yau proved this to be true.
9. This illustration is courtesy of Andrew Hanson of Indiana University, and was made using the Mathematica 3-D graphing package.
10. For the mathematically inclined reader we note that this particular Calabi-Yau space is a real three-dimensional slice through the quintic hypersurface in complex projective four-space.
Chapter 9
1. Edward Witten, "Reflections on the Fate of Spacetime" Physics Today, April 1996, p. 24.
2. Interview with Edward Witten, May 11, 1998.
3. Sheldon Glashow and Paul Ginsparg, "Desperately Seeking Superstrings?" Physics Today, May 1986, p. 7.
4. Sheldon Glashow, in The Superworld I, ed. A. Zichichi (New York: Plenum, 1990), p. 250.
5. Sheldon Glashow, Interactions (New York: Warner Books, 1988), p. 335.
6. Richard Feynman, in Superstrings: A Theory of Everything? ed. Paul Davies and Julian Brown (Cambridge, Eng: Cambridge University Press, 1988).
7. Howard Georgi, in The New Physics, ed. Paul Davies (Cambridge: Cambridge University Press 1989), p. 446.
8. Interview with Edward Witten, March 4, 1998.
9. Interview with Cumrun Vafa, January 12, 1998.
10. Murray Gell-Mann, as quoted in Robert P. Crease and Charles C. Mann, The Second Creation (New Brunswick, N.J.: Rutgers University Press), 1996, p. 414.
11. Interview with Sheldon Glashow, December 28, 1997.
12. Interview with Sheldon Glashow, December 28, 1997.
13. Interview with Howard Georgi, December 28, 1997. During the interview, Georgi also noted that the experimental refutation of the prediction of proton decay that emerged from his and Glashow's first proposed grand unified theory (see Chapter 7) played a significant part in his reluctance to embrace superstring theory. He noted poignantly that his grand unified theory invoked a vastly higher energy realm than any theory previously considered, and when its prediction was proved wrong—when it resulted in his "being slapped down by nature"—his attitude toward studying extremely high energy physics abruptly changed. When I asked him whether experimental confirmation of his grand unified theory might have inspired him to lead the charge to the Planck scale, he responded, "Yes, it likely would have."
14. David Gross, "Superstrings and Unification," in Proceedings of the XXIV International Conference on High Energy Physics, ed. R. Kotthaus and J. Kühn (Berlin: Springer-Verlag, 1988), p. 329.
15. Having said this, it's worth bearing in mind the long-shot possibility, pointed out in endnote 8 of Chapter 6, that strings just might be significantly longer than originally thought and therefore might be subject to direct experimental observation by accelerators within a few decades.
16. For the mathematically inclined reader we note that the more precise mathematical statement is that the number of families is half the absolute value of the Euler number of the Calabi-Yau space. The Euler number itself is the alternating sum of the dimensions of the manifold's homology groups—the latter being what we loosely refer to as multidimensional holes. So, three families emerge from Calabi-Yau spaces whose Euler number is ±6.
17. Interview with John Schwarz, December 23, 1997.
18. For the mathematically inclined reader we note that we are referring to Calabi-Yau manifolds with a finite, nontrivial fundamental group, the order of which, in certain cases, determines the fractional charge denominators.
19. Interview with Edward Witten, March 4, 1998.
20. For the expert we note that some of these processes violate lepton number conservation as well as charge-parity-time (CPT) reversal symmetry.
Chapter 10
1. For completeness, we note that although much of what we have covered to this point in the book applies equally well to open strings (a string with loose ends) or closed-string loops (the strings on which we have focused), the topic discussed here is one in which the two kinds of strings would appear to have different properties. After all, an open string will not get entangled by looping around a circular dimension. Nevertheless, through work that ultimately has played a pivotal part in the second superstring revolution, in 1989 Joe Polchinski from the University of California at Santa Barbara and two of his students, Jian-Hui Dai and Robert Leigh, showed how open strings fit perfectly into the conclusions we find in this chapter.
2. In case you are wondering why the possible uniform vibrational energies are whole number multiples of 1/R, you need only think back to the discussion of quantum mechanics—the warehouse in particular—from Chapter 4. There we learned that quantum mechanics implies that energy, like money, comes in discrete lumps: whole number multiples of various energy denominations. In the case of uniform vibrational string motion in the Garden-hose universe, this energy denomination is precisely 1/R, as we demonstrated in the text using the uncertainty principle. Thus the uniform vibrational energies are whole number multiples of 1/R.
3. Mathematically, the identity between the string energies in a universe with a circular dimension whose radius is either R or 1/R arises from the fact that the energies are of the form v/R + wR, where vis the vibration number and w is the winding number. This equation is invariant under the simultaneous interchange of v and w as well as R and 1/R—i.e., under the interchange of vibration and winding numbers and inversion of the radius. In our discussion we are working in Planck units, but we can work in more conventional units by rewriting the energy formula in terms of 
—the so-called string scale—whose value is about the Planck length, 10-33 centimeter. We can then express string energies as v/R + wR/, which is invariant under interchange of v and w as well as R and /R, where the latter two are now expressed in terms of conventional units of distance.
4. You may be wondering how it's possible for a string that stretches all the way around a circular dimension of radius R to nevertheless measure the radius to be 1/R. Although a thoroughly justifiable concern, its resolution actually lies in the imprecise phrasing of the question itself. You see, when we say that the string is wrapped around a circle of radius R, we are by necessity invoking a definition of distance (so that the phrase "radius R" has meaning). But this definition of distance is the one relevant for the unwound string modes—that is, the vibration modes. From the point of view of this definition of distance—and only this definition—the winding string configurations appear to stretch around the circular part of space. However, from the second definition of distance, the one that caters to the wound-string configurations, they are every bit as localized in space as are the vibration modes from the viewpoint of the first definition of distance, and the radius they "see" is 1/R, as discussed in the text. This description gives some sense of why wound and unwound strings measure distances that are inversely related. But as the point is quite subtle, it is perhaps worth noting the underlying technical analysis for the mathematically inclined reader. In ordinary point-particle quantum mechanics, distance and momentum (essentially energy) are related by Fourier transform. That is, a position eigenstate |x> on a circle of radius Rcan be defined by |x>=
veixp|p> where p = v/R and |p> is a momentum eigenstate (the direct analog of what we have called a uniform-vibration mode of a string—overall motion without change in shape). In string theory, though, there is a second notion of position eigenstate |
> defined by making use of the winding string states: |>= we
|
> where |> is a winding eigenstate with = wR. From these definitions we immediately see that x is periodic with period 2
R while is periodic with period 2/R, showing that x is a position coordinate on a circle of radius R while is the position coordinate on a circle of radius 1/R. Even more explicitly, we can now imagine taking the two wavepackets |x> and |>, both starting say, at the origin, and allowing them to evolve in time to carry out our operational approach for defining distance. The radius of the circle, as measured by either probe, is then proportional to the required time lapse for the packet to return to its initial configuration. Since a state with energy E evolves with a phase factor involving Et, we see that the time lapse, and hence the radius, is t ~ 1/E ~ R for the vibration modes and t ~ 1/E ~1/R for the winding modes.
5. For the mathematically inclined reader, we note that, more precisely, the number of families of string vibrations is one-half the absolute value of the Euler characteristic of the Calabi-Yau space, as mentioned in note 16 of Chapter 9. This is given by the absolute value of difference between h2,1 and h1,1, where hp,q denotes the (p,q) Hodge number. Up to a numerical shift, these count the number of nontrivial homology three-cycles ("three-dimensional holes") and the number of homology two-cycles ("two-dimensional holes"). And so, whereas we speak of the total number of holes in the main text, the more precise analysis shows that the number of families depends on the absolute value of difference between the odd-and even-dimensional holes. The conclusion, however, is the same. For instance, if two Calabi-Yau spaces differ by the interchange of their respective h2,1 and h1,1 Hodge numbers, the number of particle families—and the total number of "holes"—will not change.
6. The name comes from the fact that the "Hodge diamonds"—a mathematical summary of the holes of various dimensions in a Calabi-Yau space—for each Calabi-Yau space of a mirror pair are mirror reflections of one another.
7. The term mirror symmetry is also used in other, completely different contexts in physics, such as in the question of chirality—that is, whether the universe is left-right symmetric—as discussed in note 7 of Chapter 8.
Chapter 11
1. The mathematically inclined reader will recognize that we are asking whether the topology of space is dynamical—that is, whether it can change. We note that although we will often use the language of dynamical topology change, in practice we are usually considering a one-parameter family of spacetimes whose topology changes as a function of the parameter. Technically speaking, this parameter is not time, but in certain limits can essentially be identified with time.
2. For the mathematically inclined reader, the procedure involves blowing down rational curves on a Calabi-Yau manifold and then making use of the fact that, under certain circumstances, the resulting singularity can be repaired by distinct small resolutions.
3. K. C. Cole, New York Times Magazine, October 18, 1987, p. 20.
Chapter 12
1. Albert Einstein, as quoted in John D. Barrow, Theories of Everything (New York: Fawcett-Columbine, 1992), p. 13.
2. Let's briefly summarize the differences between the five string theories. To do so, we note that vibrational disturbances along a loop of string can travel clockwise or counterclockwise. The Type IIA and Type IIB strings differ in that in the latter theory, these clockwise/counterclockwise vibrations are identical, while in the former, they are exactly opposite in form. Opposite has a precise mathematical meaning in this context, but it's easiest to think about in terms of the spins of the resulting vibrational patterns in each theory. In the Type IIB theory, it turns out that all particles spin in the same direction (they have the same chirality), whereas in the Type IIA theory, they spin in both directions (they have both chiralities). Nevertheless, each theory incorporates supersymmetry. The two heterotic theories differ in a similar but more dramatic way. Each of their clockwise string vibrations looks like those of the Type II string (when focusing on just the clockwise vibrations, the Type IIA and Type IIB theories are the same), but their counterclockwise vibrations are those of the original bosonic string theory. Although the bosonic string has insurmountable problems when chosen for both clockwise and counterclockwise string vibrations, in 1985 David Gross, Jeffrey Harvey, Emil Martinec, and Ryan Rhom (all then at Princeton University and dubbed the "Princeton String Quartet") showed that a perfectly sensible theory emerges if it is used in combination with the Type II string. The really odd feature of this union is that it has been known since the work of Claude Lovelace of Rutgers University in 1971 and the work of Richard Brower of Boston University, Peter Goddard of Cambridge University, and Charles Thorn of the University of Florida at Gainesville in 1972 that the bosonic string requires a 26-dimensional spacetime, whereas the superstring, as we have discussed, requires a 10-dimensional one. So the heterotic string constructions are a strange hybrid—a heterosis—in which counterclockwise vibrational patterns live in 26 dimensions and clockwise patterns live in 10 dimensions! Before you get caught up in trying to make sense of this perplexing union, Gross and his collaborators showed that the extra 16 dimensions on the bosonic side must be curled up into one of two very special higher-dimensional doughnutlike shapes, giving rise to the Heterotic-O and Heterotic-E theories. Since the extra 16 dimensions on the bosonic side are rigidly curled up, each of these theories behaves as though it really has 10 dimensions, just as in the Type II case. Again, both heterotic theories incorporate a version of supersymmetry. Finally, the Type I theory is a close cousin of the Type IIB string except that, in addition to the closed loops of string we have discussed in previous chapters, it also has strings with unconnected ends—so-called open strings.
3. When we speak of "exact" answers in this chapter, such as the "exact" motion of the earth, what we really mean is the exact prediction for some physical quantity within some chosen theoretical framework. Until we truly have the final theory—perhaps we now do, perhaps we never will—all of our theories will themselves be approximations to reality. But this notion of approximate has nothing to do with our discussion in this chapter. Here we are concerned with the fact that within a chosen theory, it is often difficult, if not impossible, to extract the exact predictions that the theory makes. Instead, we have to extract such predictions using approximation methods based on a perturbative approach.
4. These diagrams are string theory versions of the so-called Feynman diagrams, invented by Richard Feynman for performing perturbative calculations in point-particle quantum field theory.
5. More precisely, every virtual string pair, that is, every loop in a given diagram, contributes—among other more complicated terms—a multiplicative factor of the string coupling constant. More loops translate into more factors of the string coupling constant. If the string coupling constant is less than 1, repeated multiplications make the overall contribution ever smaller; if it is 1 or larger, repeated multiplications yield a contribution with the same or larger magnitude.
6. For the mathematically inclined reader, we note that the equation states that spacetime must admit a Ricci-flat metric. If we split spacetime into a Cartesian product of four-dimensional Minkowski spacetime and a six-dimensional compact Kähler space, Ricci-flatness is equivalent to the latter being a Calabi-Yau manifold. This is why Calabi-Yau spaces play such a prominent role in string theory.
7. Of course, nothing absolutely ensures that these indirect approaches are justified. For example, just as some faces are not left-right symmetric, it might be that the laws of physics are different in other far-flung regions of the universe, as we will discuss briefly in Chapter 14.
8. The expert reader will recognize that these statements require so-called N=2 supersymmetry.
9. To be a little more precise, if we call the Heterotic-O coupling constant gHO and the Type I coupling constant gI, then the relation between the two theories states that they are physically identical so long as gHO = 1/gI, which is equivalent to gI = 1/gHO. When one coupling constant is big the other is small.
10. This is a close analog of the R, 1/R duality discussed previously. If we call the Type IIB string coupling constant gIIB then the statement that appears to be true is that the values gIIB and 1/gIIBdescribe the same physics. If gIIB is big, 1/gIIB is small, and vice versa.
11. If all but four dimensions are curled up, a theory with more than eleven total dimensions necessarily gives rise to massless particles with spin greater than 2, something that both theoretical and experimental considerations rule out.
12. A notable exception is the important 1987 work of Duff, Paul Howe, Takeo Inami, and Kelley Stelle in which they drew on earlier insights of Eric Bergshoeff, Ergin Sezgin, and Townsend to argue that ten-dimensional string theory should have a deep eleven-dimensional connection.
13. More precisely, this diagram should be interpreted as saying that we have a single theory that depends on a number of parameters. The parameters include coupling constants as well as geometrical size and shape parameters. In principle, we should be able to use the theory to calculate particular values for all of these parameters—a particular value for its coupling constant and a particular form for the spacetime geometry—but within our current theoretical understanding, we do not know how to accomplish this. And so, to understand the theory better string theorists study its properties as the values of these parameters are varied over all possibilities. If the parameter values are chosen to lie in any of the six peninsular regions of Figure 12.11, the theory has the properties inherent to one of the five string theories, or to eleven-dimensional supergravity, as marked. If the parameter values are chosen to lie in the central region, the physics is governed by the still mysterious M-theory.
14. We should note, though, that even in the peninsular regions there are some exotic ways in which branes can have an effect on familiar physics. For example, it has been suggested that our three extended spatial dimensions might themselves be a three-brane that is large and unfurled. If so, as we go about our daily business we would be gliding through the interior of a three-dimensional membrane. Investigations of such possibilities are now being undertaken.
15. Interview with Edward Witten, May 11, 1998.
Chapter 13
1. The expert reader will recognize that under mirror symmetry, a collapsing three-dimensional sphere on one Calabi-Yau space gets mapped to a collapsing two-dimensional sphere on the mirror Calabi-Yau space—apparently putting us back in the situation of flops discussed in Chapter 11. The difference, however, is that a mirror rephrasing of this sort results in the antisymmetric tensor field Bµv—the real part of the complexified Kähler form on the mirror Calabi-Yau space—vanishing, and this is a far more drastic sort of singularity than that discussed in Chapter 11.
2. More precisely, these are examples of extremal black holes: black holes that have the minimum mass consistent with the force charges they carry, just like the BPS states in Chapter 12. Similar black holes will also play a pivotal role in the following discussion on black hole entropy.
3. The radiation emitted from a black hole should be just like that emitted from a hot oven—the very problem, discussed at the outset of Chapter 4, that played such a pivotal role in the development of quantum mechanics.
4. It turns out that because the black holes involved in space-tearing conifold transitions are extremal, they do not Hawking radiate, regardless of how light they become.
5. Stephen Hawking, lecture at Amsterdam Symposium on Gravity, Black Holes, and Strings, June 21, 1996.
6. In their initial calculation, Strominger and Vafa found that the mathematics was made easier by working with five—not four—extended spacetime dimensions. Surprisingly, after completing their calculation of the entropy of such a five-dimensional black hole they realized that no theoretician had as yet constructed such hypothetical extremal black holes in the setting of five-dimensional general relativity. Since only by comparing their answer to the area of the event horizon of such a hypothetical black hole could they confirm their results, Strominger and Vafa then set out to mathematically construct such a five-dimensional black hole. They succeeded. It was then a simple matter to show that the microscopic string theory calculation of the entropy was in agreement with what Hawking would have predicted based on the area of the black hole's event horizon. But it is interesting to realize that because the black hole solution was found later, Strominger and Vafa did not know the answer they were shooting for while undertaking their entropy calculation. Since their work, numerous researchers, led most notably by Princeton physicist Curtis Callan, have succeeded in extending the entropy calculations to the more familiar setting of four extended spacetime dimensions, and all are in agreement with Hawking's predictions.
7. Interview with Sheldon Glashow, December 29, 1997.
8. Laplace, Philosophical Essay on Probabilities, trans. Andrew I. Dale (New York: Springer-Verlag, 1995).
9. Stephen Hawking, in Hawking and Roger Penrose, The Nature of Space and Time (Princeton: Princeton University Press, 1995), p. 41.
10. Stephen Hawking, lecture at the Amsterdam Symposium on Gravity, Black Holes, and Strings, June 21, 1997.
11. Interview with Andrew Strominger, December 29, 1997.
12. Interview with Cumrun Vafa, January 12, 1998.
13. Stephen Hawking, lecture at the Amsterdam Symposium on Gravity, Black Holes, and Strings, June 21, 1997.
14. This issue also has some bearing on the information-loss question, as some physicists have speculated over the years that there might be a central "nugget" embedded in the depths of a black hole that stores all of the information carried by matter that gets trapped within the hole's horizon.
15. In fact, the space-tearing conifold transitions discussed in this chapter involve black holes and hence might seem to be tied up with the question of their singularities. But recall that the conifold tear occurs just as the black hole has shed all its mass, and is therefore not directly related to questions concerning black hole singularities.
Chapter 14
1. More precisely, the universe should be filled with photons conforming to the radiation thermally emitted by a perfectly absorbent body—a "black-body" in the language of thermodynamics—with the stated temperature range. This is the same radiation spectrum emitted quantum mechanically by black holes, as explained by Hawking, and by a hot oven, as explained by Planck.
2. The discussion conveys the spirit of the issues involved although we are glossing over some subtle features having to do with the motion of light in an expanding universe that affect the detailed numerics. In particular, although special relativity declares that nothing can travel faster than the speed of light, this does not preclude two photons carried along on the expanding spatial fabric from receeding from one another at a speed exceeding that of light. For example, at the time the universe first became transparent, about 300,000 years ATB, locations in the heavens that were about 900,000 light-years apart would have been able to have influenced each other, even though the distance between them exceeds 300,000 light-years. The extra factor of three comes from the expansion of the spatial fabric. This means that as we run the cosmic film backward in time, by the time we get to 300,000 years ATB, two points in the heavens need only be less than 900,000 light-years apart to have had a chance to influence each other's temperature. These detailed numerics do not change the qualitative features of the issues discussed.
3. For a detailed and lively discussion of the discovery of the inflationary cosmological model and the problems it resolves, see Alan Guth, The Inflationary Universe (Reading, Mass: Addison-Wesley, 1997).
4. For the mathematically inclined reader, we note that the idea underlying this conclusion is the following: If the sum of the spacetime dimensions of the paths swept out by each of two objects is greater than or equal to the spacetime dimension of the arena through which they are moving then they will generically intersect. For instance, point particles sweep out one-dimensional spacetime paths—the sum of the spacetime dimensions for two such particle paths is therefore two. The spacetime dimension of Lineland is also two, and hence their paths will generally intersect (assuming their velocities have not been finely tuned to be exactly equal). Similarly, strings sweep out two-dimensional spacetime paths (their world-sheets); for two strings the sum in question is therefore four. This means that strings moving in four spacetime dimensions (three space and one time) will generally intersect.
5. With the discovery of M-theory and the recognition of an eleventh dimension, string theorists have begun studying ways of curling up all seven extra dimensions in a manner that puts them all on more or less equal footing. The possible choices for such seven-dimensional manifolds are known as Joyce manifolds, after Domenic Joyce of Oxford University, who is credited with finding the first techniques for their mathematical construction.
6. Interview with Cumrun Vafa, January 12, 1998.
7. The expert reader will note that our description is taking place in the so-called string frame of reference, in which increasing curvature during the pre-big bang arises from (a dilaton-driven) increase in the strength of the gravitational force. In the so-called Einstein frame, the evolution would be described as an accelerating contraction phase.
8. Interview with Gabriele Veneziano, May 19, 1998.
9. Smolin's ideas are discussed in his book The Life of the Cosmos (New York: Oxford University Press, 1997).
10. Within string theory, for example, this evolution could be driven by small changes to the shape of the curled-up dimensions from one universe to its offspring. From our results on space-tearing conifold transitions, we know that a sufficiently long sequence of such small changes can take us from one Calabi-Yau to any other, allowing the multiverse to sample the reproductive efficiency of all universes based on strings. After the multiverse has passed through sufficiently many stages of reproduction, Smolin's hypothesis would lead us to expect that the typical universe will have a Calabi-Yau component that is optimized for fertility.
Chapter 15
1. Interview with Edward Witten, March 4, 1998.
2. Some theorists see a hint of this idea in the holographic principle, a concept originated by Susskind and the renowned Dutch physicist Gerard 't Hooft. Just as a hologram can reproduce a three-dimensional visual image from a specially designed two-dimensional film, Susskind and 't Hooft have suggested that all of the physical happenings we encounter may actually be encoded fully through equations defined in a lower-dimensional world. Although this may sound as strange as trying to draw someone's portrait by viewing only their shadow, we can get a sense of what it means, and understand part of Susskind's and 't Hooft's motivation, by thinking about black hole entropy as discussed in Chapter 13. Recall that the entropy of a black hole is determined by the surface area of its event horizon—and not by the total volume of space that the event horizon bounds. Therefore, the disorder of a black hole, and correspondingly the information it can embody, is encoded in the two-dimensional data of surface area. It is almost as if the event horizon of the black hole acts like a hologram by capturing all the information content of the black hole's three-dimensional interior. Susskind and 't Hooft have generalized this idea to the whole universe by suggesting that everything that occurs in the "interior" of the universe is merely a reflection of data and equations defined on a distant, bounding surface. Recently, work by the Harvard physicist Juan Maldacena, together with important subsequent work by Witten and of Princeton physicists Steven Gubser, Igor Klebanov, and Alexander Polyakov, has shown that, at least in certain cases, string theory embodies the holographic principle. In a manner that is currently being investigated vigorously, it appears that the physics of a universe governed by string theory has an equivalent description that involves only physics that takes place on such a bounding surface—a surface necessarily of lower dimensionality than the interior. Some string theorists have suggested that fully understanding the holographic principle and its role in string theory may well lead to the third superstring revolution.
3. Sir Isaac Newton's Mathematical Principles of Natural Philosophy and His System of the World, trans. Motte and Cajori (Berkeley: University of California Press, 1962), Vol. I, p. 6.
4. If you are familiar with linear algebra, one simple and relevant way of thinking about noncommutative geometry is to replace conventional Cartesian coordinates, which commute under multiplication, with matrices, which do not.
5. Interview with Cumrun Vafa, January 12, 1998.
6. Interview with Edward Witten, May 11, 1998.
7. Quoted in Banesh Hoffman with Helen Dukas, Albert Einstein, Creator and Rebel (New York: Viking, 1972), p. 18.
8. Martin J. Klein, "Einstein: The Life and Times, by R. W. Clark," (book review) Science 174, pp. 1315-16.
9. Jacob Bronkowski, The Ascent of Man (Boston: Little, Brown, 1973), p. 20.