Chaos: Making a New Science - James Gleick (1988)

The Experimenter

It’s an experience like no other experience I can describe, the best thing that can happen to a scientist, realizing that something that’s happened in his or her mind exactly corresponds to something that happens in nature. It’s startling every time it occurs. One is surprised that a construct of one’s own mind can actually be realized in the honest-to-goodness world out there. A great shock, and a great, great joy.

—LEO KADANOFF

“ALBERT IS GETTING MATURE.” So they said at École Normale Supérieure, the academy which, with École Polytechnique, sits atop the French educational hierarchy. They wondered whether age was taking its toll on Albert Libchaber, who had made a distinguished name for himself as a low-temperature physicist, studying the quantum behavior of superfluid helium at temperatures a breath away from absolute zero. He had prestige and a secure place on the faculty. And now in 1977 he was wasting his time and the university’s resources on an experiment that seemed trivial. Libchaber himself worried that he would be jeopardizing the career of any graduate student he employed on such a project, so he got the assistance of a professional engineer instead.

Five years before the Germans invaded Paris, Libchaber was born there, the son of Polish Jews, the grandson of a rabbi. He survived the war the same way Benoit Mandelbrot did, by hiding in the countryside, separated from his parents because their accents were too dangerous. His parents managed to survive; the rest of the family was lost to the Nazis. In a quirk of political fate, Libchaber’s own life was saved by the protection of a local chief of the Pétain secret police, a man whose fervent right-wing beliefs were matched only by his fervent antiracism. After the war, the ten-year-old boy returned the favor. He testified, only half-comprehending, before a war crimes commission, and his testimony saved the man.

Moving through the world of French academic science, Libchaber rose in his profession, his brilliance never questioned. His colleagues did sometimes think he was a little crazy—a Jewish mystic amid the rationalists, a Gaullist where most scientists were Communists. They joked about his Great Man theory of history, his fixation on Goethe, his obsession with old books. He had hundreds of original editions of works by scientists, some dating back to the 1600s. He read them not as historical curiosities but as a source of fresh ideas about the nature of reality, the same reality he was probing with his lasers and his high-technology refrigeration coils. In his engineer, Jean Maurer, he had found a compatible spirit, a Frenchman who worked only when he felt like it. Libchaber thought Maurer would find his new project amusing—his understated Gallic euphemism for intriguing or exciting or profound. The two set out in 1977 to build an experiment that would reveal the onset of turbulence.

As an experimenter, Libchaber was known for a nineteenth-century style: clever mind, nimble hands, always preferring ingenuity to brute force. He disliked giant technology and heavy computation. His idea of a good experiment was like a mathematician’s idea of a good proof. Elegance counted as much as results. Even so, some colleagues thought he was carrying things too far with his onset-of-turbulence experiment. It was small enough to carry around in a matchbox—and sometimes Libchaber did carry it around, like some piece of conceptual art. He called it “Helium in a Small Box.” The heart of the experiment was even smaller, a cell about the size of a lemon seed, carved in stainless steel with the sharpest possible edges and walls. Into the cell was fed liquid helium chilled to about four degrees above absolute zero, warm compared to Libchaber’s old superfluid experiments.

The laboratory occupied the second floor of the École physics building in Paris, just a few hundred feet from Louis Pasteur’s old laboratory. Like all good general-purpose physics laboratories, Libchaber’s existed in a state of constant mess, paint cans and hand tools strewn about on floors and tables, odd-sized pieces of metal and plastic everywhere. Amid the disarray, the apparatus that held Libchaber’s minuscule fluid cell was a striking bit of purposefulness. Below the stainless steel cell sat a bottom plate of high-purity copper. Above sat a top plate of sapphire crystal. The materials were chosen according to how they conducted heat. There were tiny electric heating coils and Teflon gaskets. The liquid helium flowed down from a reservoir, itself just a half-inch cube. The whole system sat inside a container that maintained an extreme vacuum. And that container, in turn, sat in a bath of liquid nitrogen, to help stabilize the temperature.

Vibration always worried Libchaber. Experiments, like real nonlinear systems, existed against a constant background of noise. Noise hampered measurement and corrupted data. In sensitive flows—and Libchaber’s would be as sensitive as he could make it—noise might sharply perturb a nonlinear flow, knocking it from one kind of behavior into another. But nonlinearity can stabilize a system as well as destabilize it. Nonlinear feedback regulates motion, making it more robust. In a linear system, a perturbation has a constant effect. In the presence of nonlinearity, a perturbation can feed on itself until it dies away and the system returns automatically to a stable state. Libchaber believed that biological systems used their nonlinearity as a defense against noise. The transfer of energy by proteins, the wave motion of the heart’s electricity, the nervous system—all these kept their versatility in a noisy world. Libchaber hoped that whatever structure underlay fluid flow would prove robust enough for his experiment to detect.

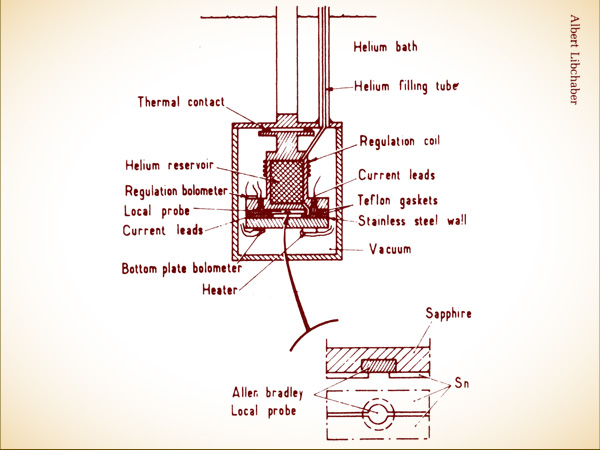
“HELIUM IN A SMALL BOX.” Albert Libchaber’s delicate experiment: Its heart was a carefully machined rectangular cell containing liquid helium; tiny sapphire “bolometers” measured the fluid’s temperature. The tiny cell was embedded in a casing designed to shield it from the noise and vibration and to allow precise control of the heating.

His plan was to create convection in the liquid helium by making the bottom plate warmer than the top plate. It was exactly the convection model described by Edward Lorenz, the classic system known as Rayleigh-Bénard convection. Libchaber was not aware of Lorenz—not yet. Nor had he any idea of Mitchell Feigenbaum’s theory. In 1977 Feigenbaum was beginning to travel the scientific lecture circuit, and his discoveries were making their mark where scientists knew how to interpret them. But as far as most physicists could tell, the patterns and regularities of Feigenbaumology bore no obvious connection to real systems. Those patterns came out of a digital calculator. Physical systems were infinitely more complicated. Without more evidence, the most anyone could say was that Feigenbaum had discovered a mathematical analogy that looked like the beginning of turbulence.

Libchaber knew that American and French experiments had weakened the Landau idea for the onset of turbulence by showing that turbulence arrived in a sudden transition, instead of a continuous piling-up of different frequencies. Experimenters like Jerry Gollub and Harry Swinney, with their flow in a rotating cylinder, had demonstrated that a new theory was needed, but they had not been able to see the transition to chaos in clear detail. Libchaber knew that no clear image of the onset of turbulence had emerged in a laboratory, and he decided that his speck of a fluid cell would give a picture of the greatest possible clarity.

A NARROWING OF VISION helps keep science moving. By their lights, fluid dynamicists were correct to doubt the high level of precision that Swinney and Gollub claimed to have achieved in Couette flow. By their lights, mathematicians were correct to resent Ruelle, as they did. He had broken the rules. He had put forward an ambitious physical theory in the guise of a tight mathematical statement. He had made it hard to separate what he assumed from what he proved. The mathematician who refuses to endorse an idea until it meets the standard of theorem, proof, theorem, proof, plays a role that his discipline has written for him: consciously or not, he is standing watch against frauds and mystics. The journal editor who rejects new ideas because they are cast in an unfamiliar style may make his victims think that he is guarding turf on behalf of his established colleagues, but he, too, has a role to play in a community with reason to beware of the untried. “Science was constructed against a lot of nonsense,” as Libchaber himself said. When his colleagues called Libchaber a mystic, the epithet was not always meant to be endearing.

He was an experimenter, careful and disciplined, known for precision in his prodding of matter. Yet he had a feeling for the abstract, ill-defined, ghostly thing called flow. Flow was shape plus change, motion plus form. A physicist, conceiving systems of differential equations, would call their mathematical movement a flow. Flow was a Platonic idea, assuming that change in systems reflected some reality independent of the particular instant. Libchaber embraced Plato’s sense that hidden forms fill the universe. “But you know that they do! You have seen leaves. When you look at all the leaves, aren’t you struck by the fact that the number of generic shapes is limited? You could easily draw the main shape. It would be of some interest to try to understand that. Or other shapes. In an experiment you have seen liquid penetrating into a liquid.” His desk was strewn with pictures of such experiments, fat fractal fingers of liquid. “Now, in your kitchen, if you turn on your gas, you see that the flame is this shape again. It’s very broad. It’s universal. I don’t care whether it’s a burning flame or a liquid in a liquid or a solid growing crystal—what I’m interested in is this shape.

“There has been since the eighteenth century some kind of dream that science was missing the evolution of shape in space and the evolution of shape in time. If you think of a flow, you can think of a flow in many ways, flow in economics or a flow in history. First it may be laminar, then bifurcating to a more complicated state, perhaps with oscillations. Then it may be chaotic.”

The universality of shapes, the similarities across scales, the recursive power of flows within flows—all sat just beyond reach of the standard differential-calculus approach to equations of change. But that was not easy to see. Scientific problems are expressed in the available scientific language. So far, the twentieth century’s best expression of Libchaber’s intuition about flow needed the language of poetry. Wallace Stevens, for example, asserted a feeling about the world that stepped ahead of the knowledge available to physicists. He had an uncanny suspicion about flow, how it repeated itself while changing:

“The flecked river

Which kept flowing and never the same way twice, flowing

Through many places, as if it stood still in one.”

Stevens’s poetry often imparts a vision of tumult in atmosphere and water. It also conveys a faith about the invisible forms that order takes in nature, a belief

“that, in the shadowless atmosphere,

The knowledge of things lay round but unperceived.”

When Libchaber and some other experimenters in the 1970s began looking into the motion of fluids, they did so with something approaching this subversive poetic intent. They suspected a connection between motion and universal form. They accumulated data in the only way possible, writing down numbers or recording them in a digital computer. But then they looked for ways to organize the data in ways that would reveal shapes. They hoped to express shapes in terms of motion. They were convinced that dynamical shapes like flames and organic shapes like leaves borrowed their form from some not-yet-understood weaving of forces. These experimenters, the ones who pursued chaos most relentlessly, succeeded by refusing to accept any reality that could be frozen motionless. Even Libchaber would not have gone so far as to express it in such terms, but their conception came close to what Stevens felt as an “insolid billowing of the solid”:

“The vigor of glory, a glittering in the veins,

As things emerged and moved and were dissolved,

Either in distance, change or nothingness,

The visible transformations of summer night,

An argentine abstraction approaching form

And suddenly denying itself away.”

FOR LIBCHABER, GOETHE, NOT STEVENS, supplied mystical inspiration. While Feigenbaum was looking through Harvard’s library for Goethe’s Theory of Colors, Libchaber had already managed to add to his collection an original edition of the even more obscure monograph On the Transformation of Plants. This was Goethe’s sidelong assault on physicists who, he believed, worried exclusively about static phenomena rather than the vital forces and flows that produce the shapes we see from instant to instant. Part of Goethe’s legacy—a negligible part, as far as literary historians were concerned—was a pseudoscientific following in Germany and Switzerland, kept alive by such philosophers as Rudolf Steiner and Theodor Schwenk. These men, too, Libchaber admired as much as a physicist could.

“Sensitive chaos”—Das sensible Chaos—was Schwenk’s phrase for the relation between force and form. He used it for the title of a strange little book first published in 1965 and falling sporadically in and out of print thereafter. It was a book first about water. The English edition carried an admiring preface from Commandant Jacques Y. Cousteau and testimonials from the Water Resources Bulletin and the Journal of the institute of Water Engineers. Little pretense at science marred Schwenk’s exposition, and none at mathematics. Yet he observed flawlessly. He laid out a multitude of natural flowing shapes with an artist’s eye. He assembled photographs and made dozens of precise drawings, like the sketches of a cell biologist peering through his first microscope. He had an open-mindedness and a naïveté that would have made Goethe proud.

Flow fills his pages. Great rivers like the Mississippi and the Bassin d’Arcachon in France meander in wide curves to the sea. In the sea itself, the Gulf Stream, too, meanders, making loops that swing east and west. It is a giant river of warm water amid cold, as Schwenk said, a river that “builds its own banks out of the cold water itself.” When the flow itself is past or invisible, the evidence of flow remains. Rivers of air leave their mark on the desert sand, showing the waves. The flow of the ebbing tide inscribes a network of veins on a beach. Schwenk did not believe in coincidence. He believed in universal principles, and, more than universality, he believed in a certain spirit in nature that made his prose uncomfortably anthropomorphic. His “archetypal principle” was this: that flow “wants to realize itself, regardless of the surrounding material.”

Within currents, he knew, there are secondary currents. Water moving down a meandering river flows, secondarily, around the river’s axis, toward one bank, down to the riverbed, across toward the other bank, up toward the surface, like a particle spiraling around a doughnut. The trail of any water particle forms a string twisting around other strings. Schwenk had a topologist’s imagination for such patterns. “This picture of strands twisted together in a spiral is only accurate with respect to the actual movement. One does often speak of ‘strands’ of water; they are however not really single strands but whole surfaces, interweaving spatially and flowing past each other.” He saw rhythms competing in waves, waves overtaking one another, dividing surfaces, and boundary layers. He saw eddies and vortices and vortex trains, understanding them as the “rolling” of one surface about another. Here he came as close as a philosopher could to the physicist’s conception of the dynamics of approaching turbulence. His artistic conviction assumed universality. To Schwenk, vortices meant instability, and instability meant that a flow was fighting an inequality within itself, and the inequality was “archetypal.” The rolling of eddies, the unfurling of ferns, the creasing of mountain ranges, the hollowing of animal organs all followed one path, as he saw it. It had nothing to do with any particular medium, or any particular kind of difference. The inequalitiescould be slow and fast, warm and cold, dense and tenuous, salt and fresh, viscous and fluid, acid and alkaline. At the boundary, life blossoms.

Life, though, was D’Arcy Wentworth Thompson’s territory. This extraordinary naturalist wrote in 1917: “It may be that all the laws of energy, and all the properties of matter, and all the chemistry of all the colloids are as powerless to explain the body as they are impotent to comprehend the soul. For my part, I think not.” D’Arcy Thompson brought to the study of life exactly what Schwenk, fatally, lacked: mathematics. Schwenk argued by analogy. His case—spiritual, flowering, encyclopedic—finally came down to a display of similarities. D’Arcy Thompson’s masterwork, On Growth and Form, shared something of Schwenk’s mood and something of his method. The modern reader wonders how much to credit the meticulous pictures of multipronged falling droplets of liquid, hanging in sinuous tendrils, displayed next to astonishingly similar living jellyfish. Is this just a highbrow case of coincidence? If two forms look alike, must we look for like causes?

D’Arcy Thompson surely stands as the most influential biologist ever left on the fringes of legitimate science. The twentieth century’s revolution in biology, well under way in his lifetime, passed him by utterly. He ignored chemistry, misunderstood the cell, and could not have predicted the explosive development of genetics. His writing, even in his time, seemed too classical and literary—too beautiful—to be reliably scientific. No modern biologist has to read D’Arcy Thompson. Yet somehow the greatest biologists find themselves drawn to his book. Sir Peter Medawar called it “beyond comparison the finest work of literature in all the annals of science that have been recorded in the English tongue.” Stephen Jay Gould found no place better to turn for the intellectual pedigree of his own growing sense that nature constrains the shapes of things. Apart from D’Arcy Thompson, not many modern biologists had pursued the undeniable unity of living organisms. “Few had asked whether all the patterns might be reduced to a single system of generating forces,” as Gould put it. “And few seemed to sense what significance such a proof of unity might possess for the science of organic form.”

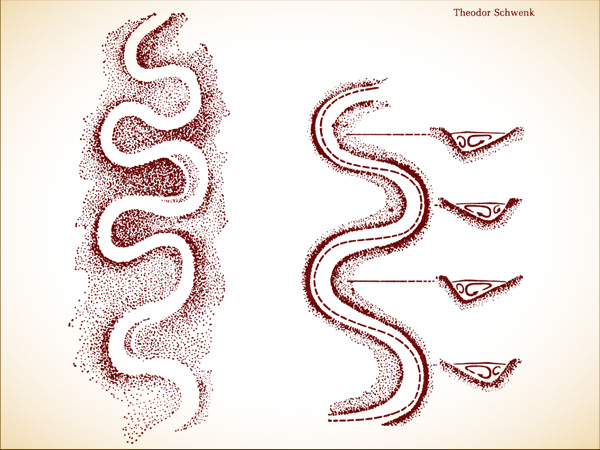
MEANDERING AND SPIRALING FLOWS. Theodor Schwenk depicted the currents of natural flows as strands with complicated secondary motions. “They are however not really single strands,” he wrote, “but whole surfaces, interweaving spatially.…”

DROPS DESCENDING. D’Arcy Wentworth Thompson showed the hanging threads and columns made by ink drops falling through water (left) and by jellyfish (right). “An extremely curious result…is to show how sensitive these…drops are to physical conditions. For using the same gelatine all the while, and merely varying the density of the fluid in the third decimal place, we obtain a whole range of configurations, from the ordinary hanging drop to the same with a ribbed pattern….”

This classicist, polyglot, mathematician, zoologist tried to see life whole, just as biology was turning so productively toward methods that reduced organisms to their constituent functioning parts. Reductionism triumphed, most thrillingly in molecular biology but everywhere else as well, from evolution to medicine. How else to understand cells but by understanding membranes and nuclei and ultimately proteins, enzymes, chromosomes, and base pairs? When biology finally broached the interior workings of sinuses, retinas, nerves, brain tissue, it became unamusingly quaint to care about the shape of the skull. D’Arcy Thompson was the last to do so. He was also the last great biologist for many years to devote rhetorical energy to a careful discussion of cause, particularly the distinction between final cause and efficient or physical cause. Final cause is cause based on purpose or design: a wheel is round because that shape makes transportation possible. Physical cause is mechanical: the earth is round because gravity pulls a spinning fluid into a spheroid. The distinction is not always so obvious. A drinking glass is round because that is the most comfortable shape to hold or drink from. A drinking glass is round because that is the shape naturally assumed by spun pottery or blown glass.

In science, on the whole, physical cause dominates. Indeed, as astronomy and physics emerged from the shadow of religion, no small part of the pain came from discarding arguments by design, forward-looking teleology—the earth is what it is so that humanity can do what it does. In biology, however, Darwin firmly established teleology as the central mode of thinking about cause. The biological world may not fulfill God’s design, but it fulfills a design shaped by natural selection. Natural selection operates not on genes or embryos, but on the final product. So an adaptationist explanation for the shape of an organism or the function of an organ always looks to its cause, not its physical cause but its final cause. Final cause survives in science wherever Darwinian thinking has become habitual. A modern anthropologist speculating about cannibalism or ritual sacrifice tends, rightly or wrongly, to ask only what purpose it serves. D’Arcy Thompson saw this coming. He begged that biology remember physical cause as well, mechanism and teleology together. He devoted himself to explaining the mathematical and physical forces that work on life. As adaptationism took hold, such explanations came to seem irrelevant. It became a rich and fruitful problem to explain a leaf in terms of how natural selection shaped such an effective solar panel. Only much later did some scientists start to puzzle again over the side of nature left unexplained. Leaves come in just a few shapes, of all the shapes imaginable; and the shape of a leaf is not dictated by its function.

The mathematics available to D’Arcy Thompson could not prove what he wanted to prove. The best he could do was draw, for example, skulls of related species with a crosshatching of coordinates, demonstrating that a simple geometric transformation turned one into the other. For simple organisms—with shapes so tantalizingly reminiscent of liquid jets, droplet splashes, and other manifestations of flow—he suspected physical causes, such as gravity and surface tension, that just could not do the formative work he asked of them. Why then, was Albert Libchaber thinking about On Growth and Form when he began his fluid experiments?

D’Arcy Thompson’s intuition about the forces that shape life came closer than anything in the mainstream of biology to the perspective of dynamical systems. He thought of life as life, always in motion, always responding to rhythms—the “deep-seated rhythms of growth” which he believed created universal forms. He considered his proper study not just the material forms of things but their dynamics—“the interpretation, in terms of force, of the operations of Energy.” He was enough of a mathematician to know that cataloguing shapes proved nothing. But he was enough of a poet to trust that neither accident nor purpose could explain the striking universality of forms he had assembled in his long years of gazing at nature. Physical laws must explain it, governing force and growth in ways that were just out of understanding’s reach. Plato again. Behind the particular, visible shapes of matter must lie ghostly forms serving as invisible templates. Forms in motion.

LIBCHABER CHOSE LIQUID HELIUM for his experiment. Liquid helium has exceedingly low viscosity, so it will roll at the slightest push. The equivalent experiment in a medium-viscosity fluid like water or air would have taken a much larger box. With low viscosity, Libchaber made his experiment that much more sensitive to heating. To cause convection in his millimeter-wide cell, he had only to create a temperature difference of a thousandth of a degree between the top and bottom surfaces. That was why the cell had to be so tiny. In a larger box, where the liquid helium would have more room to roll, the equivalent motion would require even less heating, much less. In a box ten times larger in each direction, the size of a grape—a thousand times greater in volume—convection would begin with a heat differential of a millionth of a degree. Such minute temperature variations could not be controlled.

In the planning, in the design, in the construction, Libchaber and his engineer devoted themselves to eliminating any hint of messiness. In fact, they did all they could to eliminate the motion they were trying to study. Fluid motion, from smooth flow to turbulence, is thought of as motion through space. Its complexity appears as a spatial complexity, its disturbances and vortices as a spatial chaos. But Libchaber was looking for rhythms that would expose themselves as change over time. Time was the playing field and the yardstick. He squeezed space down nearly to a one-dimensional point. He was bringing to an extreme a technique that his predecessors in fluid experimentation had used, too. Everyone knew that an enclosed flow—Rayleigh-Bénard convection in a box or Couette-Taylor rotation in a cylinder—behaved measurably better than an open flow, like waves in the ocean or the air. In open flow, the boundary surface remains free, and the complexity multiplies.

Since convection in a rectilinear box produces rolls of fluid like hot dogs—or in this case like sesame seeds—he chose the dimensions of his cell carefully to allow precisely enough room for two rolls. The liquid helium would rise in the center, turn up and over to the left and right, and then descend on the outside edges of the cell. It was an arrested geometry. The wobbling would be confined. Clean lines and careful proportions would eliminate any extraneous fluctuations. Libchaber froze the space so that he could play with the time.

Once the experiment began, the helium rolling inside the cell inside the vacuum container inside the nitrogen bath, Libchaber would need some way to see what was happening. He embedded two microscopic temperature probes in the sapphire upper surface of the cell. Their output was recorded continuously by a pen plotter. Thus he could monitor the temperatures at two spots at the top of the fluid. It was so sensitive, so clever, another physicist said, that Libchaber succeeded in cheating nature.

This miniature masterpiece of precision took two years to explore fully, but it was, as he said, the right brush for his painting, not too grand or sophisticated. He finally saw everything. Running his experiment hour after hour, night and day, Libchaber found a more intricate pattern of behavior in the onset of turbulence than he had ever imagined. The full period-doubling cascade appeared. Libchaber confined and purified the motion of a fluid that rises when heated. The process begins with the first bifurcation, the onset of motion as soon as the bottom plate of high-purity copper heats up enough to overcome the tendency of the fluid to remain still. At a few degrees above absolute zero, a mere one-thousandth of a degree is enough. The liquid at the bottom warms and expands enough to become lighter than the cool liquid above. To let the warm liquid rise, the cool liquid must sink. Immediately, to let both motions occur, the liquid organizes itself into a pair of rolling cylinders. The rolls reach a constant speed, and the system settles into an equilibrium—a moving equilibrium, with heat energy being converted steadily into motion and dissipating through friction back to heat and passing out through the cool top plate.

So far, Libchaber was reproducing a well-known experiment in fluid mechanics, so well known that it was disdained. “It was classical physics,” he said, “which unfortunately meant it was old, which meant it was uninteresting.” It also happened to be precisely the flow that Lorenz had modeled with his system of three equations. But a real-world experiment—real liquid, a box cut by a machinist, a laboratory subject to the vibrations of Parisian traffic—already made the task of collecting data far more troublesome than simply generating numbers by a computer.

Experimenters like Libchaber used a simple pen plotter to record the temperature, as measured by a probe embedded in the top surface. In the equilibrium motion after the first bifurcation, the temperature at any one point remains steady, more or less, and the pen records a straight line. With more heating, more instability sets in. A kink develops in each roll, and the kink moves steadily back and forth. This wobble shows up as a changing temperature, up and down between two values. The pen now draws a wavy line across the paper.

From a simple temperature line, changing continuously and shaken by experimental noise, it becomes impossible to read the exact timing of new bifurcations or to deduce their nature. The line makes erratic peaks and valleys that seem almost as random as a stock market fever line. Libchaber analyzed such data by turning it into a spectrum diagram, meant to reveal the main frequencies hidden in the changing temperatures. Making a spectrum diagram of data from an experiment is like graphing the sound frequencies that make up a complex chord in a symphony. An uneven line of fuzziness always runs across the bottom of the graph—experimental noise. The main tones show up as vertical spikes: the louder the tone, the higher the spike. Similarly, if the data produce a dominant frequency—a rhythm peaking once a second, for example—then that frequency will show up as a spike on a spectrum diagram.

In Libchaber’s experiment, as it happened, the first wavelength to appear was about two seconds. The next bifurcation brought a subtle change. The roll continued to wobble and the bolometer temperature continued to rise and fall with a dominant rhythm. But on odd cycles the temperature started going a bit higher than before, and on even cycles a bit lower. In fact, the maximum temperature split in two, so that there were two different maximums and two minimums. The pen line, though hard to read, developed a wobble on top of a wobble—a metawobble. On the spectrum diagram, that showed up more clearly. The old frequency was still strongly present, since the temperature still rose every two seconds. Now, however, a new frequency appeared at exactly half the old frequency, because the system had developed a component that repeated every four seconds. As the bifurcations continued, it was possible to distinguish a strangely consistent pattern: new frequencies appeared at double the old, so that the diagram filled in the quarters and the eighths and the sixteenths, starting to resemble a picket fence with alternating short and tall pickets.

Even to a man looking for hidden forms in messy data, tens and then hundreds of runs were necessary before the habits of this tiny cell started to come clear. Peculiar things could always happen as Libchaber and his engineer slowly turned up the temperature and the system settled from one equilibrium into another. Sometimes transient frequencies would appear, slide slowly across the spectrum diagram, and disappear. Sometimes, the clean geometry notwithstanding, three rolls would develop instead of two—and how could they know, really, what was happening inside that tiny cell?

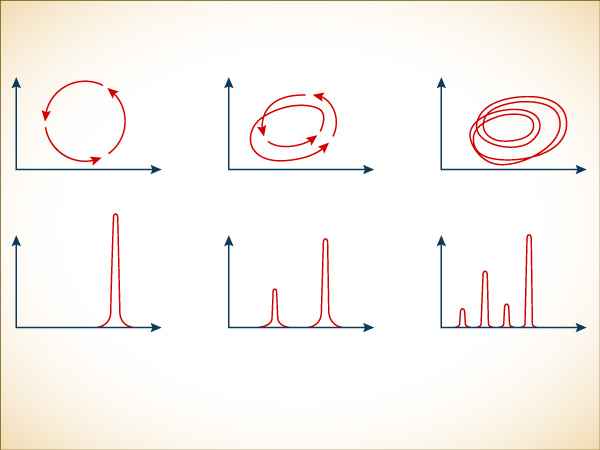
TWO WAYS OF SEEING A BIFURCATION. When an experiment like Libchaber’s convection cell produces a steady oscillation, its phase-space portrait is a loop, repeating itself at regular intervals (top left). An experimenter measuring the frequencies in the data will see a spectrum diagram with a strong spike for this single rhythm. After a period-doubling bifurcation, the system loops twice before repeating itself exactly (center), and now the experimenter sees a new rhythm at half the frequency—twice the period—of the original. New period-doublings fill in the spectrum diagram with more spikes.

IF LIBCHABER HAD KNOWN then of Feigenbaum’s discovery of universality, he would have known exactly where to look for his bifurcations and what to call them. By 1979 a growing group of mathematicians and mathematically inclined physicists were paying attention to Feigenbaum’s new theory. But the mass of scientists familiar with the problems of real physical systems believed that they had good reason to withhold judgment. Complexity was one thing in the one-dimensional systems, the maps of May and Feigenbaum. It was surely something else in the two- or three- or four-dimensional systems of mechanical devices that an engineer could build. Those required serious differential equations, not just simple difference equations. And another chasm seemed to divide those low-dimensional systems from systems of fluid flow, which physicists thought of as potentially infinite-dimensional systems. Even a cell like Libchaber’s, so carefully structured, had a virtual infinitude of fluid particles. Each particle represented at least the potential for independent motion. In some circumstances, any particle might be the locus of some new twist or vortex.

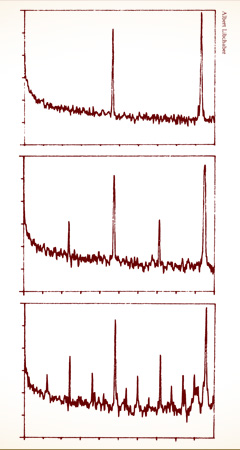
REAL-WORLD DATA CONFIRMING THEORY. Libchaber’s spectrum diagrams showed vividly the precise pattern of period-doubling predicted by theory. The spikes of new frequencies stand out clearly above the experimental noise. Feigenbaum’s scaling theory predicted not only when and where the new frequencies would arrive but also how strong they would be-their amplitudes.

“The notion that the actual relevant meat-and-potatoes motion in such a system boils down to maps—nobody understood that,” said Pierre Hohenberg of AT&T Bell Laboratories in New Jersey. Hohenberg became one of the very few physicists to follow the new theory and the new experiments together. “Feigenbaum may have dreamt of that, but he certainly didn’t say it. Feigenbaum’s work was about maps. Why should physicists be interested in maps?—it’s a game. Really, as long as they were playing around with maps, it seemed pretty remote from what we wanted to understand.

“But when it was seen in experiments, that’s when it really became exciting. The miracle is that, in systems that are interesting, you can still understand behavior in detail by a model with a small number of degrees of freedom.”

It was Hohenberg, in the end, who brought the theorist and the experimenter together. He ran a workshop at Aspen in the summer of 1979, and Libchaber was there. (Four years earlier, at the same summer workshop, Feigenbaum had listened to Steve Smale talk about a number—just a number—that seemed to pop up when a mathematician looked at the transition to chaos in a certain equation.) When Libchaber described his experiments with liquid helium, Hohenberg took note. On his way home, Hohenberg happened to stop and see Feigenbaum in New Mexico. Not long after, Feigenbaum paid a call on Libchaber in Paris. They stood amid the scattered parts and instruments of Libchaber’s laboratory. Libchaber proudly displayed his tiny cell and let Feigenbaum explain his latest theory. Then they walked through the Paris streets looking for the best possible cup of coffee. Libchaber remembered later how surprised he was to see a theorist so young and so, he would say, lively.

THE LEAP FROM MAPS TO FLUID FLOW seemed so great that even those most responsible sometimes felt it was like a dream. How nature could tie such complexity to such simplicity was far from obvious. “You have to regard it as a kind of miracle, not like the usual connection between theory and experiment,” Jerry Gollub said. Within a few years, the miracle was being repeated again and again in a vast bestiary of laboratory systems: bigger fluid cells with water and mercury, electronic oscillators, lasers, even chemical reactions. Theorists adapted Feigenbaum’s techniques and found other mathematical routes to chaos, cousins of period-doubling: such patterns as intermittency and quasiperiodicity. These, too, proved universal in theory and experiment.

The experimenters’ discoveries helped set in motion the era of computer experimentation. Physicists discovered that computers produced the same qualitative pictures as real experiments, and produced them millions of times faster and more reliably. To many, even more convincing than Libchaber’s results was a fluid model created by Valter Franceschini of the University of Modena, Italy—a system of five differential equations that produced attractors and period-doubling. Franceschini knew nothing of Feigenbaum, but his complex, many-dimensional model produced the same constants Feigenbaum had found in one-dimensional maps. In 1980 a European group provided a convincing mathematical explanation: dissipation bleeds a complex system of many conflicting motions, eventually bringing the behavior of many dimensions down to one.

Outside of computers, to find a strange attractor in a fluid experiment remained a serious challenge. It occupied experimenters like Harry Swinney well into the 1980s. And when the experimenters finally succeeded, the new computer experts often belittled their results as just the rough, predictable echoes of the magnificently detailed pictures their graphics terminals were already churning out. In a computer experiment, when you generated your thousands or millions of data points, patterns made themselves more or less apparent. In a laboratory, as in the real world, useful information had to be distinguished from noise. In a computer experiment data flowed like wine from a magic chalice. In a laboratory experiment you had to fight for every drop.

Still, the new theories of Feigenbaum and others would not have captured so wide a community of scientists on the strength of computer experiments alone. The modifications, the compromises, the approximations needed to digitize systems of nonlinear differential equations were too suspect. Simulations break reality into chunks, as many as possible but always too few. A computer model is just a set of arbitrary rules, chosen by programmers. A real-world fluid, even in a stripped-down millimeter cell, has the undeniable potential for all the free, untrammeled motion of natural disorder. It has the potential for surprise.

In the age of computer simulation, when flows in everything from jet turbines to heart valves are modeled on supercomputers, it is hard to remember how easily nature can confound an experimenter. In fact, no computer today can completely simulate even so simple a system as Libchaber’s liquid helium cell. Whenever a good physicist examines a simulation, he must wonder what bit of reality was left out, what potential surprise was sidestepped. Libchaber liked to say that he would not want to fly in a simulated airplane—he would wonder what had been missed. Furthermore, he would say that computer simulations help to build intuition or to refine calculations, but they do not give birth to genuine discovery. This, at any rate, is the experimenter’s creed. His experiment was so immaculate, his scientific goals so abstract, that there were still physicists who considered Libchaber’s work more philosophy or mathematics than physics. He believed, in turn, that the ruling standards of his field were reductionist, giving primacy to the properties of atoms. “A physicist would ask me, How does this atom come here and stick there? And what is the sensitivity to the surface? And can you write the Hamiltonian of the system?

“And if I tell him, I don’t care, what interests me is this shape, the mathematics of the shape and the evolution, the bifurcation from this shape to that shape to this shape, he will tell me, that’s not physics, you are doing mathematics. Even today he will tell me that. Then what can I say? Yes, of course, I am doing mathematics. But it is relevant to what is around us. That is nature, too.”

The patterns he found were indeed abstract. They were mathematical. They said nothing about the properties of liquid helium or copper or about the behavior of atoms near absolute zero. But they were the patterns that Libchaber’s mystical forebears had dreamed of. They made legitimate a realm of experimentation in which many scientists, from chemists to electrical engineers, soon became explorers, seeking out the new elements of motion. The patterns were there to see the first time he succeeded in raising the temperature enough to isolate the first period-doubling, and the next, and the next. According to the new theory, the bifurcations should have produced a geometry with precise scaling, and that was just what Libchaber saw, the universal Feigenbaum constants turning in that instant from a mathematical ideal to a physical reality, measurable and reproducible. He remembered the feeling long afterward, the eerie witnessing of one bifurcation after another and then the realization that he was seeing an infinite cascade, rich with structure. It was, as he said, amusing.