Chaos: Making a New Science - James Gleick (1988)

A Geometry of Nature

And yet relation appears,

A small relation expanding like the shade

Of a cloud on sand, a shape on the side of a hill.

—WALLACE STEVENS
“Connoisseur of Chaos”

A PICTURE OF REALITY built up over the years in Benoit Mandelbrot’s mind. In 1960, it was a ghost of an idea, a faint, unfocused image. But Mandelbrot recognized it when he saw it, and there it was on the blackboard in Hendrik Houthakker’s office.

Mandelbrot was a mathematical jack-of-all-trades who had been adopted and sheltered by the pure research wing of the International Business Machines Corporation. He had been dabbling in economics, studying the distribution of large and small incomes in an economy. Houthakker, a Harvard economics professor, had invited Mandelbrot to give a talk, and when the young mathematician arrived at Littauer Center, the stately economics building just north of Harvard Yard, he was startled to see his findings already charted on the older man’s blackboard. Mandelbrot made a querulous joke—how should my diagram have materialized ahead of my lecture?—but Houthakker didn’t know what Mandelbrot was talking about. The diagram had nothing to do with income distribution; it represented eight years of cotton prices.

From Houthakker’s point of view, too, there was something strange about this chart. Economists generally assumed that the price of a commodity like cotton danced to two different beats, one orderly and one random. Over the long term, prices would be driven steadily by real forces in the economy—the rise and fall of the New England textile industry, or the opening of international trade routes. Over the short term, prices would bounce around more or less randomly. Unfortunately, Houthakker’s data failed to match his expectations. There were too many large jumps. Most price changes were small, of course, but the ratio of small changes to large was not as high as he had expected. The distribution did not fall off quickly enough. It had a long tail.

The standard model for plotting variation was and is the bell-shaped curve. In the middle, where the hump of the bell rises, most data cluster around the average. On the sides, the low and high extremes fall off rapidly. A statistician uses a bell-shaped curve the way an internist uses a stethoscope, as the instrument of first resort. It represents the standard, so-called Gaussian distribution of things—or, simply, the normal distribution. It makes a statement about the nature of randomness. The point is that when things vary, they try to stay near an average point and they manage to scatter around the average in a reasonably smooth way. But as a means of finding paths through the economic wilderness, the standard notions left something to be desired. As the Nobel laureate Wassily Leontief put it, “In no field of empirical inquiry has so massive and sophisticated a statistical machinery been used with such indifferent results.”

No matter how he plotted them, Houthakker could not make the changes in cotton prices fit the bell-shaped model. But they made a picture whose silhouette Mandelbrot was beginning to see in surprisingly disparate places. Unlike most mathematicians, he confronted problems by depending on his intuition about patterns and shapes. He mistrusted analysis, but he trusted his mental pictures. And he already had the idea that other laws, with different behavior, could govern random, stochastic phenomena. When he went back to the giant IBM research center in Yorktown Heights, New York, in the hills of northern Westchester County, he carried Houthakker’s cotton data in a box of computer cards. Then he sent to the Department of Agriculture in Washington for more, dating back to 1900.

THE BELL-SHAPED CURVE.

Like scientists in other fields, economists were crossing the threshold into the computer era, slowly realizing that they would have the power to collect and organize and manipulate information on a scale that had been unimaginable before. Not all kinds of information were available, though, and information that could be rounded up still had to be turned into some usable form. The keypunch era was just beginning, too. In the hard sciences, investigators found it easier to amass their thousands or millions of data points. Economists, like biologists, dealt with a world of willful living beings. Economists studied the most elusive creatures of all.

But at least the economists’ environment produced a constant supply of numbers. From Mandelbrot’s point of view, cotton prices made an ideal data source. The records were complete and they were old, dating back continuously a century or more. Cotton was a piece of the buying-and-selling universe with a centralized market—and therefore centralized record-keeping—because at the turn of the century all the South’s cotton flowed through the New York exchange on route to New England, and Liverpool’s prices were linked to New York’s as well.

Although economists had little to go on when it came to analyzing commodity prices or stock prices, that did not mean they lacked a fundamental viewpoint about how price changes worked. On the contrary, they shared certain articles of faith. One was a conviction that small, transient changes had nothing in common with large, long-term changes. Fast fluctuations come randomly. The small-scale ups and downs during a day’s transactions are just noise, unpredictable and uninteresting. Long-term changes, however, are a different species entirely. The broad swings of prices over months or years or decades are determined by deep macroeconomic forces, the trends of war or recession, forces that should in theory give way to understanding. On the one hand, the buzz of short-term fluctuation; on the other, the signal of long-term change.

As it happened, that dichotomy had no place in the picture of reality that Mandelbrot was developing. Instead of separating tiny changes from grand ones, his picture bound them together. He was looking for patterns not at one scale or another, but across every scale. It was far from obvious how to draw the picture he had in mind, but he knew there would have to be a kind of symmetry, not a symmetry of right and left or top and bottom but rather a symmetry of large scales and small.

Indeed, when Mandelbrot sifted the cotton-price data through IBM’s computers, he found the astonishing results he was seeking. The numbers that produced aberrations from the point of view of normal distribution produced symmetry from the point of view of scaling. Each particular price change was random and unpredictable. But the sequence of changes was independent of scale: curves for daily price changes and monthly price changes matched perfectly. Incredibly, analyzed Mandelbrot’s way, the degree of variation had remained constant over a tumultuous sixty-year period that saw two World Wars and a depression.

Within the most disorderly reams of data lived an unexpected kind of order. Given the arbitrariness of the numbers he was examining, why, Mandelbrot asked himself, should any law hold at all? And why should it apply equally well to personal incomes and cotton prices?

In truth, Mandelbrot’s background in economics was as meager as his ability to communicate with economists. When he published an article on his findings, it was preceded by an explanatory article by one of his students, who repeated Mandelbrot’s material in economists’ English. Mandelbrot moved on to other interests. But he took with him a growing determination to explore the phenomenon of scaling. It seemed to be a quality with a life of its own—a signature.

INTRODUCED FOR A LECTURE years later (“…taught economics at Harvard, engineering at Yale, physiology at the Einstein School of Medicine…”), he remarked proudly: “Very often when I listen to the list of my previous jobs I wonder if I exist. The intersection of such sets is surely empty.” Indeed, since his early days at IBM, Mandelbrot has failed to exist in a long list of different fields. He was always an outsider, taking an unorthodox approach to an unfashionable corner of mathematics, exploring disciplines in which he was rarely welcomed, hiding his grandest ideas in efforts to get his papers published, surviving mainly on the confidence of his employers in Yorktown Heights. He made forays into fields like economics and then withdrew, leaving behind tantalizing ideas but rarely well-founded bodies of work.

In the history of chaos, Mandelbrot made his own way. Yet the picture of reality that was forming in his mind in 1960 evolved from an oddity into a full-fledged geometry. To the physicists expanding on the work of people like Lorenz, Smale, Yorke, and May, this prickly mathematician remained a sideshow—but his techniques and his language became an inseparable part of their new science.

The description would not have seemed apt to anyone who knew him in his later years, with his high imposing brow and his list of titles and honors, but Benoit Mandelbrot is best understood as a refugee. He was born in Warsaw in 1924 to a Lithuanian Jewish family, his father a clothing wholesaler, his mother a dentist. Alert to geopolitical reality, the family moved to Paris in 1936, drawn in part by the presence of Mandelbrot’s uncle, Szolem Mandelbrojt, a mathematician. When the war came, the family stayed just ahead of the Nazis once again, abandoning everything but a few suitcases and joining the stream of refugees who clogged the roads south from Paris. They finally reached the town of Tulle.

For a while Benoit went around as an apprentice toolmaker, dangerously conspicuous by his height and his educated background. It was a time of unforgettable sights and fears, yet later he recalled little personal hardship, remembering instead the times he was befriended in Tulle and elsewhere by schoolteachers, some of them distinguished scholars, themselves stranded by the war. In all, his schooling was irregular and discontinuous. He claimed never to have learned the alphabet or, more significantly, multiplication tables past the fives. Still, he had a gift.

When Paris was liberated, he took and passed the month-long oral and written admissions examination for École Normale and École Polytechnique, despite his lack of preparation. Among other elements, the test had a vestigial examination in drawing, and Mandelbrot discovered a latent facility for copying the Venus de Milo. On the mathematical sections of the test—exercises in formal algebra and integrated analysis—he managed to hide his lack of training with the help of his geometrical intuition. He had realized that, given an analytic problem, he could almost always think of it in terms of some shape in his mind. Given a shape, he could find ways of transforming it, altering its symmetries, making it more harmonious. Often his transformations led directly to a solution of the analogous problem. In physics and chemistry, where he could not apply geometry, he got poor grades. But in mathematics, questions he could never have answered using proper techniques melted away in the face of his manipulations of shapes.

The École Normale and École Polytechnique were elite schools with no parallel in American education. Together they prepared fewer than 300 students in each class for careers in the French universities and civil service. Mandelbrot began in Normale, the smaller and more prestigious of the two, but left within days for Polytechnique. He was already a refugee from Bourbaki.

Perhaps nowhere but in France, with its love of authoritarian academies and received rules for learning, could Bourbaki have arisen. It began as a club, founded in the unsettled wake of World War I by Szolem Mandelbrot and a handful of other insouciant young mathematicians looking for a way to rebuild French mathematics. The vicious demographics of war had left an age gap between university professors and students, disrupting the tradition of academic continuity, and these brilliant young men set out to establish new foundations for the practice of mathematics. The name of their group was itself an inside joke, borrowed for its strange and attractive sound—so it was later guessed—from a nineteenth-century French general of Greek origin. Bourbaki was born with a playfulness that soon disappeared.

Its members met in secrecy. Indeed, not all their names are known. Their number was fixed. When one member left, as was required at age 50, another would be elected by the remaining group. They were the best and the brightest of mathematicians, and their influence soon spread across the continent.

In part, Bourbaki began in reaction to Poincaré, the great man of the late nineteenth century, a phenomenally prolific thinker and writer who cared less than some for rigor. Poincaré would say, I know it must be right, so why should I prove it? Bourbaki believed that Poincaré had left a shaky basis for mathematics, and the group began to write an enormous treatise, more and more fanatical in style, meant to set the discipline straight. Logical analysis was central. A mathematician had to begin with solid first principles and deduce all the rest from them. The group stressed the primacy of mathematics among sciences, and also insisted upon a detachment from other sciences. Mathematics was mathematics—it could not be valued in terms of its application to real physical phenomena. And above all, Bourbaki rejected the use of pictures. A mathematician could always be fooled by his visual apparatus. Geometry was untrustworthy. Mathematics should be pure, formal, and austere.

Nor was this strictly a French development. In the United States, too, mathematicians were pulling away from the demands of the physical sciences as firmly as artists and writers were pulling away from the demands of popular taste. A hermetic sensibility prevailed. Mathematicians’ subjects became self-contained; their method became formally axiomatic. A mathematician could take pride in saying that his work explained nothing in the world or in science. Much good came of this attitude, and mathematicians treasured it. Steve Smale, even while he was working to reunite mathematics and natural science, believed, as deeply as he believed anything, that mathematics should be something all by itself. With self-containment came clarity. And clarity, too, went hand in hand with the rigor of the axiomatic method. Every serious mathematician understands that rigor is the defining strength of the discipline, the steel skeleton without which all would collapse. Rigor is what allows mathematicians to pick up a line of thought that extends over centuries and continue it, with a firm guarantee.

Even so, the demands of rigor had unintended consequences for mathematics in the twentieth century. The field develops through a special kind of evolution. A researcher picks up a problem and begins by making a decision about which way to continue. It happened that often that decision involved a choice between a path that was mathematically feasible and a path that was interesting from the point of view of understanding nature. For a mathematician, the choice was clear: he would abandon any obvious connection with nature for a while. Eventually his students would face a similar choice and make a similar decision.

Nowhere were these values as severely codified as in France, and there Bourbaki succeeded as its founders could not have imagined. Its precepts, style, and notation became mandatory. It achieved the unassailable Tightness that comes from controlling all the best students and producing a steady flow of successful mathematics. Its dominance over École Normale was total and, to Mandelbrot, unbearable. He fled Normale because of Bourbaki, and a decade later he fled France for the same reason, taking up residence in the United States. Within a few decades, the relentless abstraction of Bourbaki would begin to die of a shock brought on by the computer, with its power to feed a new mathematics of the eye. But that was too late for Mandelbrot, unable to live by Bour-baki’s formalisms and unwilling to abandon his geometrical intuition.

ALWAYS A BELIEVER in creating his own mythology, Mandelbrot appended this statement to his entry in Who’s Who: “Science would be ruined if (like sports) it were to put competition above everything else, and if it were to clarify the rules of competition by withdrawing entirely into narrowly defined specialties. The rare scholars who are nomads-by-choice are essential to the intellectual welfare of the settled disciplines.” This nomad-by-choice, who also called himself a pioneer-by-necessity, withdrew from academe when he withdrew from France, accepting the shelter of IBM’s Thomas J. Watson Research Center. In a thirty-year journey from obscurity to eminence, he never saw his work embraced by the many disciplines toward which he directed it. Even mathematicians would say, without apparent malice, that whatever Mandelbrot was, he was not one of them.

He found his way slowly, always abetted by an extravagant knowledge of the forgotten byways of scientific history. He ventured into mathematical linguistics, explaining a law of the distribution of words. (Apologizing for the symbolism, he insisted that the problem came to his attention from a book review that he retrieved from a pure mathematician’s wastebasket so he would have something to read on the Paris subway.) He investigated game theory. He worked his way in and out of economics. He wrote about scaling regularities in the distribution of large and small cities. The general framework that tied his work together remained in the background, incompletely formed.

Early in his time at IBM, soon after his study of commodity prices, he came upon a practical problem of intense concern to his corporate patron. Engineers were perplexed by the problem of noise in telephone lines used to transmit information from computer to computer. Electric current carries the information in discrete packets, and engineers knew that the stronger they made the current the better it would be at drowning out noise. But they found that some spontaneous noise could never be eliminated. Once in a while it would wipe out a piece of signal, creating an error.

Although by its nature the transmission noise was random, it was well known to come in clusters. Periods of errorless communication would be followed by periods of errors. By talking to the engineers, Mandelbrot soon learned that there was a piece of folklore about the errors that had never been written down, because it matched none of the standard ways of thinking: the more closely they looked at the clusters, the more complicated the patterns of errors seemed. Mandelbrot provided a way of describing the distribution of errors that predicted exactly the observed patterns. Yet it was exceedingly peculiar. For one thing, it made it impossible to calculate an average rate of errors—an average number of errors per hour, or per minute, or per second. On average, in Mandelbrot’s scheme, errors approached infinite sparseness.

His description worked by making deeper and deeper separations between periods of clean transmission and periods of errors. Suppose you divided a day into hours. An hour might pass with no errors at all. Then an hour might contain errors. Then an hour might pass with no errors.

But suppose you then divided the hour with errors into smaller periods of twenty minutes. You would find that here, too, some periods would be completely clean, while some would contain a burst of errors. In fact, Mandelbrot argued—contrary to intuition—that you could never find a time during which errors were scattered continuously. Within any burst of errors, no matter how short, there would always be periods of completely error-free transmission. Furthermore, he discovered a consistent geometric relationship between the bursts of errors and the spaces of clean transmission. On scales of an hour or a second, the proportion of error-free periods to error-ridden periods remained constant. (Once, to Mandelbrot’s horror, a batch of data seemed to contradict his scheme—but it turned out that the engineers had failed to record the most extreme cases, on the assumption that they were irrelevant.)

Engineers had no framework for understanding Mandelbrot’s description, but mathematicians did. In effect, Mandelbrot was duplicating an abstract construction known as the Cantor set, after the nineteenth-century mathematician Georg Cantor. To make a Cantor set, you start with the interval of numbers from zero to one, represented by a line segment. Then you remove the middle third. That leaves two segments, and you remove the middle third of each (from one-ninth to two-ninths and from seven-ninths to eight-ninths). That leaves four segments, and you remove the middle third of each—and so on to infinity. What remains? A strange “dust” of points, arranged in clusters, infinitely many yet infinitely sparse. Mandelbrot was thinking of transmission errors as a Cantor set arranged in time.

This highly abstract description had practical weight for scientists trying to decide between different strategies of controlling error. In particular, it meant that, instead of trying to increase signal strength to drown out more and more noise, engineers should settle for a modest signal, accept the inevitability of errors and use a strategy of redundancy to catch and correct them. Mandelbrot also changed the way IBM’s engineers thought about the cause of noise. Bursts of errors had always sent the engineers looking for a man sticking a screwdriver somewhere. But Mandelbrot’s scaling patterns suggested that the noise would never be explained on the basis of specific local events.

Mandelbrot turned to other data, drawn from the world’s rivers. Egyptians have kept records of the height of the Nile for millennia. It is a matter of more than passing concern. The Nile suffers unusually great variation, flooding heavily in some years and subsiding in others. Mandelbrot classified the variation in terms of two kinds of effects, common in economics as well, which he called the Noah and Joseph Effects.

The Noah Effect means discontinuity: when a quantity changes, it can change almost arbitrarily fast. Economists traditionally imagined that prices change smoothly—rapidly or slowly, as the case may be, but smoothly in the sense that they pass through all the intervening levels on their way from one point to another. That image of motion was borrowed from physics, like much of the mathematics applied to economics. But it was wrong. Prices can change in instantaneous jumps, as swiftly as a piece of news can flash across a teletype wire and a thousand brokers can change their minds. A stock market strategy was doomed to fail, Mandelbrot argued, if it assumed that a stock would have to sell for $50 at some point on its way down from $60 to $10.

THE CANTOR DUST. Begin with a line; remove the middle third; then remove the middle third of the remaining segments; and so on. The Cantor set is the dust of points that remains. They are infinitely many, but their total length is 0.

The paradoxical qualities of such constructions disturbed nineteenth-century mathematicians, but Mandelbrot saw the Cantor set as a model for the occurrence of errors in an electronic transmission line. Engineers saw periods of error-free transmission, mixed with periods when errors would come in bursts. Looked at more closely, the bursts, too, contained error-free periods within them. And so on—it was an example of fractal time. At every time scale, from hours to seconds, Mandelbrot discovered that the relationship of errors to clean transmission remained constant. Such dusts, he contended, are indispensable in modeling intermittency.

The Joseph Effect means persistence. There came seven years of great plenty throughout the land of Egypt. And there shall arise after them seven years of famine. If the Biblical legend meant to imply periodicity, it was oversimplified, of course. But floods and droughts do persist. Despite an underlying randomness, the longer a place has suffered drought, the likelier it is to suffer more. Furthermore, mathematical analysis of the Nile’s height showed that persistence applied over centuries as well as over decades. The Noah and Joseph Effects push in different directions, but they add up to this: trends in nature are real, but they can vanish as quickly as they come.

Discontinuity, bursts of noise, Cantor dusts—phenomena like these had no place in the geometries of the past two thousand years. The shapes of classical geometry are lines and planes, circles and spheres, triangles and cones. They represent a powerful abstraction of reality, and they inspired a powerful philosophy of Platonic harmony. Euclid made of them a geometry that lasted two millennia, the only geometry still that most people ever learn. Artists found an ideal beauty in them, Ptolemaic astronomers built a theory of the universe out of them. But for understanding complexity, they turn out to be the wrong kind of abstraction.

Clouds are not spheres, Mandelbrot is fond of saying. Mountains are not cones. Lightning does not travel in a straight line. The new geometry mirrors a universe that is rough, not rounded, scabrous, not smooth. It is a geometry of the pitted, pocked, and broken up, the twisted, tangled, and intertwined. The understanding of nature’s complexity awaited a suspicion that the complexity was not just random, not just accident. It required a faith that the interesting feature of a lightning bolt’s path, for example, was not its direction, but rather the distribution of zigs and zags. Mandelbrot’s work made a claim about the world, and the claim was that such odd shapes carry meaning. The pits and tangles are more than blemishes distorting the classic shapes of Euclidian geometry. They are often the keys to the essence of a thing.

What is the essence of a coastline, for example? Mandelbrot asked this question in a paper that became a turning point for his thinking: “How Long Is the Coast of Britain?”

Mandelbrot had come across the coastline question in an obscure posthumous article by an English scientist, Lewis F. Richardson, who groped with a surprising number of the issues that later became part of chaos. He wrote about numerical weather prediction in the 1920s, studied fluid turbulence by throwing a sack of white parsnips into the Cape Cod Canal, and asked in a 1926 paper, “Does the Wind Possess a Velocity?” (“The question, at first sight foolish, improves on acquaintance,” he wrote.) Wondering about coastlines and wiggly national borders, Richardson checked encyclopedias in Spain and Portugal, Belgium and the Netherlands and discovered discrepancies of twenty percent in the estimated lengths of their common frontiers.

Mandelbrot’s analysis of this question struck listeners as either painfully obvious or absurdly false. He found that most people answered the question in one of two ways: “I don’t know, it’s not my field,” or “I don’t know, but I’ll look it up in the encyclopedia.”

In fact, he argued, any coastline is—in a sense—infinitely long. In another sense, the answer depends on the length of your ruler. Consider one plausible method of measuring. A surveyor takes a set of dividers, opens them to a length of one yard, and walks them along the coastline. The resulting number of yards is just an approximation of the true length, because the dividers skip over twists and turns smaller than one yard, but the surveyor writes the number down anyway. Then he sets the dividers to a smaller length—say, one foot—and repeats the process. He arrives at a somewhat greater length, because the dividers will capture more of the detail and it will take more than three one-foot steps to cover the distance previously covered by a one-yard step. He writes this new number down, sets the dividers at four inches, and starts again. This mental experiment, using imaginary dividers, is a way of quantifying the effect of observing an object from different distances, at different scales. An observer trying to estimate the length of England’s coastline from a satellite will make a smaller guess than an observer trying to walk its coves and beaches, who will make a smaller guess in turn than a snail negotiating every pebble.

A FRACTAL SHORE. A computer-generated coastline: the details are random, but the fractal dimension is constant, so the degree of roughness or irregularity looks the same no matter how much the image is magnified.

Common sense suggests that, although these estimates will continue to get larger, they will approach some particular final value, the true length of the coastline. The measurements should converge, in other words. And in fact, if a coastline were some Euclidean shape, such as a circle, this method of summing finer and finer straight-line distances would indeed converge. But Mandelbrot found that as the scale of measurement becomes smaller, the measured length of a coastline rises without limit, bays and peninsulas revealing ever-smaller subbays and subpeninsulas—at least down to atomic scales, where the process does finally come to an end. Perhaps.

SINCE EUCLIDEAN MEASUREMENTS—length, depth, thickness—failed to capture the essence of irregular shapes, Mandelbrot turned to a different idea, the idea of dimension. Dimension is a quality with a much richer life for scientists than for non-scientists. We live in a three-dimensional world, meaning that we need three numbers to specify a point: for example, longitude, latitude, and altitude. The three dimensions are imagined as directions at right angles to one another. This is still the legacy of Euclidean geometry, where space has three dimensions, a plane has two, a line has one, and a point has zero.

The process of abstraction that allowed Euclid to conceive of one- or two-dimensional objects spills over easily into our use of everyday objects. A road map, for all practical purposes, is a quintessentially two-dimensional thing, a piece of a plane. It uses its two dimensions to carry information of a precisely two-dimensional kind. In reality, of course, road maps are as three-dimensional as everything else, but their thickness is so slight (and so irrelevant to their purpose) that it can be forgotten. Effectively, a road map remains two-dimensional, even when it is folded up. In the same way, a thread is effectively one-dimensional and a particle has effectively no dimension at all.

Then what is the dimension of a ball of twine? Mandelbrot answered, It depends on your point of view. From a great distance, the ball is no more than a point, with zero dimensions. From closer, the ball is seen to fill spherical space, taking up three dimensions. From closer still, the twine comes into view, and the object becomes effectively one-dimensional, though the one dimension is certainly tangled up around itself in a way that makes use of three-dimensional space. The notion of how many numbers it takes to specify a point remains useful. From far away, it takes none—the point is all there is. From closer, it takes three. From closer still, one is enough—any given position along the length of twine is unique, whether the twine is stretched out or tangled up in a ball.

And on toward microscopic perspectives: twine turns to three-dimensional columns, the columns resolve themselves into one-dimensional fibers, the solid material dissolves into zero-dimensional points. Mandelbrot appealed, unmathematically, to relativity: “The notion that a numerical result should depend on the relation of object to observer is in the spirit of physics in this century and is even an exemplary illustration of it.”

But philosophy aside, the effective dimension of an object does turn out to be different from its mundane three dimensions. A weakness in Mandelbrot’s verbal argument seemed to be its reliance on vague notions, “from far away” and “a little closer.” What about in between? Surely there was no clear boundary at which a ball of twine changes from a three-dimensional to a one-dimensional object. Yet, far from being a weakness, the ill-defined nature of these transitions led to a new idea about the problem of dimensions.

Mandelbrot moved beyond dimensions 0,1,2,3…to a seeming impossibility: fractional dimensions. The notion is a conceptual high-wire act. For nonmathematicians it requires a willing suspension of disbelief. Yet it proves extraordinarily powerful.

Fractional dimension becomes a way of measuring qualities that otherwise have no clear definition: the degree of roughness or brokenness or irregularity in an object. A twisting coastline, for example, despite its immeasurability in terms of length, nevertheless has a certain characteristic degree of roughness. Mandelbrot specified ways of calculating the fractional dimension of real objects, given some technique of constructing a shape or given some data, and he allowed his geometry to make a claim about the irregular patterns he had studied in nature. The claim was that the degree of irregularity remains constant over different scales. Surprisingly often, the claim turns out to be true. Over and over again, the world displays a regular irregularity.

One wintry afternoon in 1975, aware of the parallel currents emerging in physics, preparing his first major work for publication in book form, Mandelbrot decided he needed a name for his shapes, his dimensions, and his geometry. His son was home from school, and Mandelbrot found himself thumbing through the boy’s Latin dictionary. He came across the adjective fractus, from the verb frangere, to break. The resonance of the main English cognates—fracture and fraction—seemed appropriate. Mandelbrot created the word (noun and adjective, English and French) fractal.

IN THE MIND’S EYE, a fractal is a way of seeing infinity.

Imagine a triangle, each of its sides one foot long. Now imagine a certain transformation—a particular, well-defined, easily repeated set of rules. Take the middle one-third of each side and attach a new triangle, identical in shape but one-third the size.

The result is a star of David. Instead of three one-foot segments, the outline of this shape is now twelve four-inch segments. Instead of three points, there are six.

THE KOCH SNOWFLAKE. “A rough but vigorous model of a coastline,” in Mandelbrot’s words. To construct a Koch curve, begin with a triangle with sides of length 1. At the middle of each side, add a new triangle one-third the size; and so on. The length of the boundary is 3 × 4/3 × 4/3 × 4/3…—infinity. Yet the area remains less than the area of a circle drawn around the original triangle. Thus an infinitely long line surrounds a finite area.

Now take each of the twelve sides and repeat the transformation, attaching a smaller triangle onto the middle third. Now again, and so on to infinity. The outline becomes more and more detailed, just as a Cantor set becomes more and more sparse. It resembles a sort of ideal snowflake. It is known as a Koch curve—a curve being any connected line, whether straight or round—after Helge von Koch, the Swedish mathematician who first described it in 1904.

On reflection, it becomes apparent that the Koch curve has some interesting features. For one thing, it is a continuous loop, never intersecting itself, because the new triangles on each side are always small enough to avoid bumping into each other. Each transformation adds a little area to the inside of the curve, but the total area remains finite, not much bigger than the original triangle, in fact. If you drew a circle around the original triangle, the Koch curve would never extend beyond it.

Yet the curve itself is infinitely long, as long as a Euclidean straight line extending to the edges of an unbounded universe. Just as the first transformation replaces a one-foot segment with four four-inch segments, every transformation multiplies the total length by four-thirds. This paradoxical result, infinite length in a finite space, disturbed many of the turn-of-the-century mathematicians who thought about it. The Koch curve was monstrous, disrespectful to all reasonable intuition about shapes and—it almost went without saying—pathologically unlike anything to be found in nature.

Under the circumstances, their work made little impact at the time, but a few equally perverse mathematicians imagined other shapes with some of the bizarre qualities of the Koch curve. There were Peano curves. There were Sierpiński carpets and Sierpiński gaskets. To make a carpet, start with a square, divide it three-by-three into nine equal squares, and remove the central one. Then repeat the operation on the eight remaining squares, putting a square hole in the center of each. The gasket is the same but with equilateral triangles instead of squares; it has the hard-to-imagine property that any arbitrary point is a branching point, a fork in the structure. Hard to imagine, that is, until you have thought about the Eiffel Tower, a good three-dimensional approximation, its beams and trusses and girders branching into a lattice of ever-thinner members, a shimmering network of fine detail. Eiffel, of course, could not carry the scheme to infinity, but he appreciated the subtle engineering point that allowed him to remove weight without also removing structural strength.

The mind cannot visualize the whole infinite self-embedding of complexity. But to someone with a geometer’s way of thinking about form, this kind of repetition of structure on finer and finer scales can open a whole world. Exploring these shapes, pressing one’s mental fingers into the rubbery edges of their possibilities, was a kind of playing, and Mandelbrot took a childlike delight in seeing variations that no one had seen or understood before. When they had no names, he named them: ropes and sheets, sponges and foams, curds and gaskets.

Fractional dimension proved to be precisely the right yardstick. In a sense, the degree of irregularity corresponded to the efficiency of the object in taking up space. A simple, Euclidean, one-dimensional line fills no space at all. But the outline of the Koch curve, with infinite length crowding into finite area, does fill space. It is more than a line, yet less than a plane. It is greater than one-dimensional, yet less than a two-dimensional form. Using techniques originated by mathematicians early in the century and then all but forgotten, Mandelbrot could characterize the fractional dimension precisely. For the Koch curve, the infinitely extended multiplication by four-thirds gives a dimension of 1.2618.

CONSTRUCTING WITH HOLES. A few mathematicians in the early twentieth century conceived monstrous-seeming objects made by the technique of adding or removing infinitely many parts. One such shape is the Sierpinski carpet, constructed by cutting the center one-ninth of a square; then cutting out the centers of the eight smaller squares that remain; and so on. The three-dimensional analogue is the Menger sponge, a solid-looking lattice that has an infinite surface area, yet zero volume.

In pursuing this path, Mandelbrot had two great advantages over the few other mathematicians who had thought about such shapes. One was his access to the computing resources that go with the name of IBM. Here was another task ideally suited to the computer’s particular form of high-speed idiocy. Just as meteorologists needed to perform the same few calculations at millions of neighboring points in the atmosphere, Mandelbrot needed to perform an easily programmed transformation again and again and again and again. Ingenuity could conceive of transformations. Computers could draw them—sometimes with unexpected results. The early twentieth-century mathematicians quickly reached a barrier of hard calculation, like the barrier faced by early pro-tobiologists without microscopes. In looking into a universe of finer and finer detail, the imagination can carry one only so far.

In Mandelbrot’s words: “There was a long hiatus of a hundred years where drawing did not play any role in mathematics because hand and pencil and ruler were exhausted. They were well understood and no longer in the forefront. And the computer did not exist.

“When I came in this game, there was a total absence of intuition. One had to create an intuition from scratch. Intuition as it was trained by the usual tools—the hand, the pencil, and the ruler—found these shapes quite monstrous and pathological. The old intuition was misleading. The first pictures were to me quite a surprise; then I would recognize some pictures from previous pictures, and so on.

“Intuition is not something that is given. I’ve trained my intuition to accept as obvious shapes which were initially rejected as absurd, and I find everyone else can do the same.”

Mandelbrot’s other advantage was the picture of reality he had begun forming in his encounters with cotton prices, with electronic transmission noise, and with river floods. The picture was beginning to come into focus now. His studies of irregular patterns in natural processes and his exploration of infinitely complex shapes had an intellectual intersection: a quality of self-similarity. Above all, fractal meant self-similar.

Self-similarity is symmetry across scale. It implies recursion, pattern inside of pattern. Mandelbrot’s price charts and river charts displayed self-similarity, because not only did they produce detail at finer and finer scales, they also produced detail with certain constant measurements. Monstrous shapes like the Koch curve display self-similarity because they look exactly the same even under high magnification. The self-similarity is built into the technique of constructing the curves—the same transformation is repeated at smaller and smaller scales. Self-similarity is an easily recognizable quality. Its images are everywhere in the culture: in the infinitely deep reflection of a person standing between two mirrors, or in the cartoon notion of a fish eating a smaller fish eating a smaller fish eating a smaller fish. Mandelbrot likes to quote Jonathan Swift: “So, Nat’ralists observe, a Flea/Hath smaller Fleas that on him prey,/And these have smaller Fleas to bite ’em,/ And so proceed ad infinitum.”

IN THE NORTHEASTERN United States, the best place to study earthquakes is the Lamont-Doherty Geophysical Observatory, a group of unprepossessing buildings hidden in the woods of southern New York State, just west of the Hudson River. Lamont-Doherty is where Christopher Scholz, a Columbia University professor specializing in the form and structure of the solid earth, first started thinking about fractals.

While mathematicians and theoretical physicists disregarded Mandelbrot’s work, Scholz was precisely the kind of pragmatic, working scientist most ready to pick up the tools of fractal geometry. He had stumbled across Benoit Mandelbrot’s name in the 1960s, when Mandelbrot was working in economics and Scholz was an M.I.T. graduate student spending a great deal of time on a stubborn question about earthquakes. It had been well known for twenty years that the distribution of large and small earthquakes followed a particular mathematical pattern, precisely the same scaling pattern that seemed to govern the distribution of personal incomes in a free-market economy. This distribution was observed everywhere on earth, wherever earthquakes were counted and measured. Considering how irregular and unpredictable earthquakes were otherwise, it was worthwhile to ask what sort of physical processes might explain this regularity. Or so it seemed to Scholz. Most seismologists had been content to note the fact and move on.

Scholz remembered Mandelbrot’s name, and in 1978 he bought a profusely illustrated, bizarrely erudite, equation-studded book called Fractals: Form, Chance and Dimension. It was as if Mandelbrot had collected in one rambling volume everything he knew or suspected about the universe. Within a few years this book and its expanded and refined replacement, The Fractal Geometry of Nature, had sold more copies than any other book of high mathematics. Its style was abstruse and exasperating, by turns witty, literary, and opaque. Mandelbrot himself called it “a manifesto and a casebook.”

Like a few counterparts in a handful of other fields, particularly scientists who worked on the material parts of nature, Scholz spent several years trying to figure out what to do with this book. It was far from obvious. Fractals was, as Scholz put it, “not a how-to book but a gee-whiz book.” Scholz, however, happened to care deeply about surfaces, and surfaces were everywhere in this book. He found that he could not stop thinking about the promise of Mandelbrot’s ideas. He began to work out a way of using fractals to describe, classify, and measure the pieces of his scientific world.

He soon realized that he was not alone, although it was several more years before fractals conferences and seminars began multiplying. The unifying ideas of fractal geometry brought together scientists who thought their own observations were idiosyncratic and who had no systematic way of understanding them. The insights of fractal geometry helped scientists who study the way things meld together, the way they branch apart, or the way they shatter. It is a method of looking at materials—the microscopically jagged surfaces of metals, the tiny holes and channels of porous oil-bearing rock, the fragmented landscapes of an earthquake zone.

As Scholz saw it, it was the business of geophysicists to describe the surface of the earth, the surface whose intersection with the flat oceans makes coastlines. Within the top of the solid earth are surfaces of another kind, surfaces of cracks. Faults and fractures so dominate the structure of the earth’s surface that they become the key to any good description, more important on balance than the material they run through. The fractures crisscross the earth’s surface in three dimensions, creating what Scholz whimsically called the “schizosphere.” They control the flow of fluid through the ground—the flow of water, the flow of oil, and the flow of natural gas. They control the behavior of earthquakes. Understanding surfaces was paramount, yet Scholz believed that his profession was in a quandary. In truth, no framework existed.

Geophysicists looked at surfaces the way anyone would, as shapes. A surface might be flat. Or it might have a particular shape. You could look at the outline of a Volkswagen Beetle, for example, and draw that surface as a curve. The curve would be measurable in familiar Euclidean ways. You could fit an equation to it. But in Scholz’s description, you would only be looking at that surface through a narrow spectral band. It would be like looking at the universe through a red filter—you see what is happening at that particular wavelength of light, but you miss everything happening at the wavelengths of other colors, not to mention that vast range of activity at parts of the spectrum corresponding to infrared radiation or radio waves. The spectrum, in this analogy, corresponds to scale. To think of the surface of a Volkswagen in terms of its Euclidean shape is to see it only on the scale of an observer ten meters or one hundred meters away. What about an observer one kilometer away, or one hundred kilometers? What about an observer one millimeter away, or one micron?

Imagine tracing the surface of the earth as it would look from a distance of one hundred kilometers out in space. The line goes up and down over trees and hillocks, buildings and—in a parking lot somewhere—a Volkswagen. On that scale, the surface is just a bump among many other bumps, a bit of randomness.

Or imagine looking at the Volkswagen from closer and closer, zooming in with magnifying glass and microscope. At first the surface seems to get smoother, as the roundness of bumpers and hood passes out of view. But then the microscopic surface of the steel turns out to be bumpy itself, in an apparently random way. It seems chaotic.

Scholz found that fractal geometry provided a powerful way of describing the particular bumpiness of the earth’s surface, and metallurgists found the same for the surfaces of different kinds of steel. The fractal dimension of a metal’s surface, for example, often provides information that corresponds to the metal’s strength. And the fractal dimension of the earth’s surface provides clues to its important qualities as well. Scholz thought about a classic geological formation, a talus slope on a mountainside. From a distance it is a Euclidean shape, dimension two. As a geologist approaches, though, he finds himself walking not so much on it as in it—the talus has resolved itself into boulders the size of cars. Its effective dimension has become about 2.7, because the rock surfaces hook over and wrap around and nearly fill three-dimensional space, like the surface of a sponge.

Fractal descriptions found immediate application in a series of problems connected to the properties of surfaces in contact with one another. The contact between tire treads and concrete is such a problem. So is contact in machine joints, or electrical contact. Contacts between surfaces have properties quite independent of the materials involved. They are properties that turn out to depend on the fractal quality of the bumps upon bumps upon bumps. One simple but powerful consequence of the fractal geometry of surfaces is that surfaces in contact do not touch everywhere. The bumpiness at all scales prevents that. Even in rock under enormous pressure, at some sufficiently small scale it becomes clear that gaps remain, allowing fluid to flow. To Scholz, it is the Humpty-Dumpty Effect. It is why two pieces of a broken teacup can never be rejoined, even though they appear to fit together at some gross scale. At a smaller scale, irregular bumps are failing to coincide.

Scholz became known in his field as one of a few people taking up fractal techniques. He knew that some of his colleagues viewed this small group as freaks. If he used the word fractal in the title of a paper, he felt that he was regarded either as being admirably current or not-so-admirably on a bandwagon. Even the writing of papers forced difficult decisions, between writing for a small audience of fractal aficionados or writing for a broader geophysical audience that would need explanations of the basic concepts. Still, Scholz considered the tools of fractal geometry indispensable.

“It’s a single model that allows us to cope with the range of changing dimensions of the earth,” he said. “It gives you mathematical and geometrical tools to describe and make predictions. Once you get over the hump, and you understand the paradigm, you can start actually measuring things and thinking about things in a new way. You see them differently. You have a new vision. It’s not the same as the old vision at all—it’s much broader.”

HOW BIG IS IT? How long does it last? These are the most basic questions a scientist can ask about a thing. They are so basic to the way people conceptualize the world that it is not easy to see that they imply a certain bias. They suggest that size and duration, qualities that depend on scale, are qualities with meaning, qualities that can help describe an object or classify it. When a biologist describes a human being, or a physicist describes a quark, how big and how long are indeed appropriate questions. In their gross physical structure, animals are very much tied to a particular scale. Imagine a human being scaled up to twice its size, keeping all proportions the same, and you imagine a structure whose bones will collapse under its weight. Scale is important.

The physics of earthquake behavior is mostly independent of scale. A large earthquake is just a scaled-up version of a small earthquake. That distinguishes earthquakes from animals, for example—a ten-inch animal must be structured quite differently from a one-inch animal, and a hundred-inch animal needs a different architecture still, if its bones are not to snap under the increased mass. Clouds, on the other hand, are scaling phenomena like earthquakes. Their characteristic irregularity—describable in terms of fractal dimension—changes not at all as they are observed on different scales. That is why air travelers lose all perspective on how far away a cloud is. Without help from cues such as haziness, a cloud twenty feet away can be indistinguishable from two thousand feet away. Indeed, analysis of satellite pictures has shown an invariant fractal dimension in clouds observed from hundreds of miles away.

It is hard to break the habit of thinking of things in terms of how big they are and how long they last. But the claim of fractal geometry is that, for some elements of nature, looking for a characteristic scale becomes a distraction. Hurricane. By definition, it is a storm of a certain size. But the definition is imposed by people on nature. In reality, atmospheric scientists are realizing that tumult in the air forms a continuum, from the gusty swirling of litter on a city street corner to the vast cyclonic systems visible from space. Categories mislead. The ends of the continuum are of a piece with the middle.

It happens that the equations of fluid flow are in many contexts dimensionless, meaning that they apply without regard to scale. Scaled-down airplane wings and ship propellers can be tested in wind tunnels and laboratory basins. And, with some limitations, small storms act like large storms.

Blood vessels, from aorta to capillaries, form another kind of continuum. They branch and divide and branch again until they become so narrow that blood cells are forced to slide through single file. The nature of their branching is fractal. Their structure resembles one of the monstrous imaginary objects conceived by Mandelbrot’s turn-of-the-century mathematicians. As a matter of physiological necessity, blood vessels must perform a bit of dimensional magic. Just as the Koch curve, for example, squeezes a line of infinite length into a small area, the circulatory system must squeeze a huge surface area into a limited volume. In terms of the body’s resources, blood is expensive and space is at a premium. The fractal structure nature has devised works so efficiently that, in most tissue, no cell is ever more than three or four cells away from a blood vessel. Yet the vessels and blood take up little space, no more than about five percent of the body. It is, as Mandelbrot put it, the Merchant of Venice Syndrome—not only can’t you take a pound of flesh without spilling blood, you can’t take a milligram.

This exquisite structure—actually, two intertwining trees of veins and arteries—is far from exceptional. The body is filled with such complexity. In the digestive tract, tissue reveals undulations within undulations. The lungs, too, need to pack the greatest possible surface into the smallest space. An animal’s ability to absorb oxygen is roughly proportional to the surface area of its lungs. Typical human lungs pack in a surface bigger than a tennis court. As an added complication, the labyrinth of windpipes must merge efficiently with the arteries and veins.

Every medical student knows that lungs are designed to accommodate a huge surface area. But anatomists are trained to look at one scale at a time—for example, at the millions of alveoli, microscopic sacs, that end the sequence of branching pipes. The language of anatomy tends to obscure the unity across scales. The fractal approach, by contrast, embraces the whole structure in terms of the branching that produces it, branching that behaves consistently from large scales to small. Anatomists study the vas-culatory system by classifying blood vessels into categories based on size—arteries and arterioles, veins and venules. For some purposes, those categories prove useful. But for others they mislead. Sometimes the textbook approach seems to dance around the truth: “In the gradual transition from one type of artery to another it is sometimes difficult to classify the intermediate region. Some arteries of intermediate caliber have walls that suggest larger arteries, while some large arteries have walls like those of medium-sized arteries. The transitional regions…are often designated arteries of mixed type.”

Not immediately, but a decade after Mandelbrot published his physiological speculations, some theoretical biologists began to find fractal organization controlling structures all through the body. The standard “exponential” description of bronchial branching proved to be quite wrong; a fractal description turned out to fit the data. The urinary collecting system proved fractal. The biliary duct in the liver. The network of special fibers in the heart that carry pulses of electric current to the contracting muscles. The last structure, known to heart specialists as the His-Purkinje network, inspired a particularly important line of research. Considerable work on healthy and abnormal hearts turned out to hinge on the details of how the muscle cells of the left and right pumping chambers all manage to coordinate their timing. Several chaos-minded cardiologists found that the frequency spectrum of heartbeat timing, like earthquakes and economic phenomena, followed fractal laws, and they argued that one key to understanding heartbeat timing was the fractal organization of the His-Purkinje network, a labyrinth of branching pathways organized to be self-similar on smaller and smaller scales.

How did nature manage to evolve such complicated architecture? Mandelbrot’s point is that the complications exist only in the context of traditional Euclidean geometry. As fractals, branching structures can be described with transparent simplicity, with just a few bits of information. Perhaps the simple transformations that gave rise to the shapes devised by Koch, Peano, and Sierpiński have their analogue in the coded instructions of an organism’s genes. DNA surely cannot specify the vast number of bronchi, bronchioles, and alveoli or the particular spatial structure of the resulting tree, but it can specify a repeating process of bifurcation and development. Such processes suit nature’s purposes. When E. I. DuPont de Nemours & Company and the United States Army finally began to produce a synthetic match for goose down, it was by finally realizing that the phenomenal air-trapping ability of the natural product came from the fractal nodes and branches of down’s key protein, keratin. Mandelbrot glided matter-of-factly from pulmonary and vascular trees to real botanical trees, trees that need to capture sun and resist wind, with fractal branches and fractal leaves. And theoretical biologists began to speculate that fractal scaling was not just common but universal in morphogenesis. They argued that understanding how such patterns were encoded and processed had become a major challenge to biology.

“I STARTED LOOKING in the trash cans of science for such phenomena, because I suspected that what I was observing was not an exception but perhaps very widespread. I attended lectures and looked in unfashionable periodicals, most of them of little or no yield, but once in a while finding some interesting things. In a way it was a naturalist’s approach, not a theoretician’s approach. But my gamble paid off.”

Having consolidated a life’s collection of ideas about nature and mathematical history into one book, Mandelbrot found an unaccustomed measure of academic success. He became a fixture of the scientific lecture circuit, with his indispensable trays of color slides and his wispy white hair. He began to win prizes and other professional honors, and his name became as well known to the nonscientific public as any mathematician’s. In part that was because of the aesthetic appeal of his fractal pictures; in part because the many thousands of hobbyists with microcomputers could begin exploring his world themselves. In part it was because he put himself forward. His name appeared on a little list compiled by the Harvard historian of science I. Bernard Cohen. Cohen had scoured the annals of discovery for years, looking for scientists who had declared their own work to be “revolutions.” All told, he found just sixteen. Robert Symmer, a Scots contemporary of Benjamin Franklin whose ideas about electricity were indeed radical, but wrong. Jean-Paul Marat, known today only for his bloody contribution to the French Revolution. Von Liebig. Hamilton. Charles Darwin, of course. Virchow. Cantor. Einstein. Minkowski. Von Laue. Alfred Wegener—continental drift. Compton. Just. James Watson—the structure of DNA. And Benoit Mandelbrot.

To pure mathematicians, however, Mandelbrot remained an outsider, contending as bitterly as ever with the politics of science. At the height of his success, he was reviled by some colleagues, who thought he was unnaturally obsessed with his place in history. They said he hectored them about giving due credit. Unquestionably, in his years as a professional heretic he honed an appreciation for the tactics as well as the substance of scientific achievement. Sometimes when articles appeared using ideas from fractal geometry he would call or write the authors to complain that no reference was made to him or his book.

His admirers found his ego easy to forgive, considering the difficulties he had overcome in getting recognition for his work. “Of course, he is a bit of a megalomaniac, he has this incredible ego, but it’s beautiful stuff he does, so most people let him get away with it,” one said. In the words of another: “He had so many difficulties with his fellow mathematicians that simply in order to survive he had to develop this strategy of boosting his own ego. If he hadn’t done that, if he hadn’t been so convinced that he had the right visions, then he would never have succeeded.”

The business of taking and giving credit can become obsessive in science. Mandelbrot did plenty of both. His book rings with the first person: I claim…I conceived and developed…and implemented…I have confirmed…I show…I coined…In my travels through newly opened or newly settled territory, 1 was often moved to exert the right of naming its landmarks.

Many scientists failed to appreciate this kind of style. Nor were they mollified that Mandelbrot was equally copious with his references to predecessors, some thoroughly obscure. (And all, as his detractors noted, quite safely deceased.) They thought it was just his way of trying to position himself squarely in the center, setting himself up like the Pope, casting his benedictions from one side of the field to the other. They fought back. Scientists could hardly avoid the word fractal, but if they wanted to avoid Mandelbrot’s name they could speak of fractional dimension as Hausdorff-Besicovitch dimension. They also—particularly mathematicians—resented the way he moved in and out of different disciplines, making his claims and conjectures and leaving the real work of proving them to others.

It was a legitimate question. If one scientist announces that a thing is probably true, and another demonstrates it with rigor, which one has done more to advance science? Is the making of a conjecture an act of discovery? Or is it just a cold-blooded staking of a claim? Mathematicians have always faced such issues, but the debate became more intense as computers began to play their new role. Those who used computers to conduct experiments became more like laboratory scientists, playing by rules that allowed discovery without the usual theorem-proof, theorem-proof of the standard mathematics paper.

Mandelbrot’s book was wide-ranging and stuffed with the minutiae of mathematical history. Wherever chaos led, Mandelbrot had some basis to claim that he had been there first. Little did it matter that most readers found his references obscure or even useless. They had to acknowledge his extraordinary intuition for the direction of advances in fields he had never actually studied, from seismology to physiology. It was sometimes uncanny, and sometimes irritating. Even an admirer would cry with exasperation, “Mandelbrot didn’t have everybody’s thoughts before they did.”

It hardly matters. The face of genius need not always wear an Einstein’s saintlike mien. Yet for decades, Mandelbrot believes, he had to play games with his work. He had to couch original ideas in terms that would not give offense. He had to delete his visionary-sounding prefaces to get his articles published. When he wrote the first version of his book, published in French in 1975, he felt he was forced to pretend it contained nothing too startling. That was why he wrote the latest version explicitly as “a manifesto and a casebook.” He was coping with the politics of science.

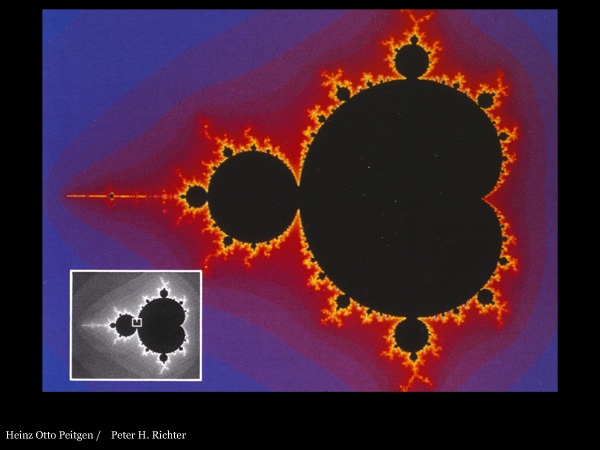
THE COMPLEX BOUNDARIES OF NEWTON’S METHOD. The attracting pull of four points—in the four dark holes—creates “basins of attraction,” each a different color, with a complicated fractal boundary. The image represents the way Newton’s method for solving equations leads from different starting points to one of four possible solutions (in this case the equation is x⁴ - 1 = 0).

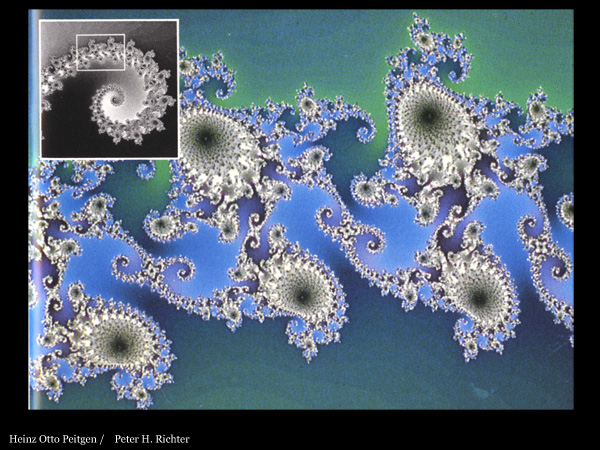
FRACTAL CLUSTERS. A random clustering of praticles generated by a computer produces a “percolation network,” one of many visual models inspired by factal geometry. Applied physicists discovered that such models imitate a variety of real-world processes, such as the formation of polymers and the diffusion of oil through factured rock. Each color in the percolation network represents a grouping that is connected throughout.

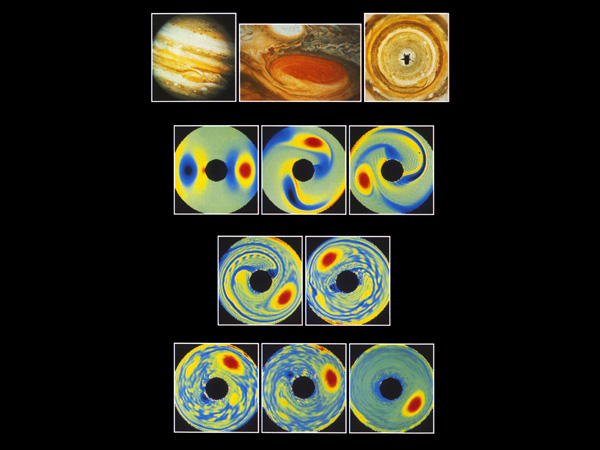
THE GREAT RED SPOT: REAL AND SIMULATED. The Voyager satellite revealed Jupiter’s surface is a seething, turbulent fluid, with horizontal bands of east-west flow. The Great Red Spot is seen from above the planet’s equator and also in a view looking down on the South Pole.
Computer graphics from Phillip Marcus’s simulation present the South Pole view. The color shows the direction of spin for particular pieces of fluid: pieces turning counterclockwise are red, and pieces turning clock-wise are blue. No matter what the staring configuration, clumps of blue tend to bread up, while the red tends ot merge into a single spot, stable and coherent amit the surrounding tumult.

“The politics affected the style in a sense which I later came to regret. I was saying, ‘It’s natural to…, It’s an interesting observation that….’ Now, in fact, it was anything but natural, and the interesting observation was in fact the result of very long investigations and search for proof and self-criticism. It had a philosophical and removed attitude which I felt was necessary to get it accepted. The politics was that, if I said I was proposing a radical departure, that would have been the end of the readers’ interest.

“Later on, I got back some such statements, people saying, ‘It is natural to observe…’ That was not what I had bargained for.”

Looking back, Mandelbrot saw that scientists in various disciplines responded to his approach in sadly predictable stages. The first stage was always the same: Who are you and why are you interested in our field? Second: How does it relate to what we have been doing, and why don’t you explain it on the basis of what we know? Third: Are you sure it’s standard mathematics? (Yes, I’m sure.) Then why don’t we know it? (Because it’s standard but very obscure.)

Mathematics differs from physics and other applied sciences in this respect. A branch of physics, once it becomes obsolete or unproductive, tends to be forever part of the past. It may be a historical curiosity, perhaps the source of some inspiration to a modern scientist, but dead physics is usually dead for good reason. Mathematics, by contrast, is full of channels and byways that seem to lead nowhere in one era and become major areas of study in another. The potential application of a piece of pure thought can never be predicted. That is why mathematicians value work in an aesthetic way, seeking elegance and beauty as artists do. It is also why Mandelbrot, in his antiquarian mode, came across so much good mathematics that was ready to be dusted off.

So the fourth stage was this: What do people in these branches of mathematics think about your work? (They don’t care, because it doesn’t add to the mathematics. In fact, they are surprised that their ideas represent nature.)

In the end, the word fractal came to stand for a way of describing, calculating, and thinking about shapes that are irregular and fragmented, jagged and broken-up—shapes from the crystalline curves of snowflakes to the discontinuous dusts of galaxies. A fractal curve implies an organizing structure that lies hidden among the hideous complication of such shapes. High school students could understand fractals and play with them; they were as primary as the elements of Euclid. Simple computer programs to draw fractal pictures made the rounds of personal computer hobbyists.

Mandelbrot found his most enthusiastic acceptance among applied scientists working with oil or rock or metals, particularly in corporate research centers. By the middle of the 1980s, vast numbers of scientists at Exxon’s huge research facility, for example, worked on fractal problems. At General Electric, fractals became an organizing principle in the study of polymers and also—though this work was conducted secretly—in problems of nuclear reactor safety. In Hollywood, fractals found their most whimsical application in the creation of phenomenally realistic landscapes, earthly and extraterrestrial, in special effects for movies.

The patterns that people like Robert May and James Yorke discovered in the early 1970s, with their complex boundaries between orderly and chaotic behavior, had unsuspected regularities that could only be described in terms of the relation of large scales to small. The structures that provided the key to nonlinear dynamics proved to be fractal. And on the most immediate practical level, fractal geometry also provided a set of tools that were taken up by physicists, chemists, seismologists, metallurgists, probability theorists and physiologists. These researchers were convinced, and they tried to convince others, that Mandelbrot’s new geometry was nature’s own.

They made an irrefutable impact on orthodox mathematics and physics as well, but Mandelbrot himself never gained the full respect of those communities. Even so, they had to acknowledge him. One mathematician told friends that he had awakened one night still shaking from a nightmare. In this dream, the mathematician was dead, and suddenly heard the unmistakable voice of God. “You know,” He remarked, “there really was something to that Mandelbrot.”

THE NOTION OF SELF-SIMILARITY strikes ancient chords in our culture. An old strain in Western thought honors the idea. Leibniz imagined that a drop of water contained a whole teeming universe, containing, in turn, water drops and new universes within. “To see the world in a grain of sand,” Blake wrote, and often scientists were predisposed to see it. When sperm were first discovered, each was thought to be a homunculus, a human, tiny but fully formed.

But self-similarity withered as a scientific principle, for a good reason. It did not fit the facts. Sperm are not merely scaled-down humans—they are far more interesting than that—and the process of ontogenetic development is far more interesting than mere enlargement. The early sense of self-similarity as an organizing principle came from the limitations on the human experience of scale. How else to imagine the very great and very small, the very fast and very slow, but as extensions of the known?

The myth died hard as the human vision was extended by telescopes and microscopes. The first discoveries were realizations that each change of scale brought new phenomena and new kinds of behavior. For modern particle physicists, the process has never ended. Every new accelerator, with its increase in energy and speed, extends science’s field of view to tinier particles and briefer time scales, and every extension seems to bring new information.

At first blush, the idea of consistency on new scales seems to provide less information. In part, that is because a parallel trend in science has been toward reductionism. Scientists break things apart and look at them one at a time. If they want to examine the interaction of subatomic particles, they put two or three together. There is complication enough. The power of self-similarity, though, begins at much greater levels of complexity. It is a matter of looking at the whole.

Although Mandelbrot made the most comprehensive geometric use of it, the return of scaling ideas to science in the 1960s and 1970s became an intellectual current that made itself felt simultaneously in many places. Self-similarity was implicit in Edward Lorenz’s work. It was part of his intuitive understanding of the fine structure of the maps made by his system of equations, a structure he could sense but not see on the computers available in 1963. Scaling also became part of a movement in physics that led, more directly than Mandelbrot’s own work, to the discipline known as chaos. Even in distant fields, scientists were beginning to think in terms of theories that used hierarchies of scales, as in evolutionary biology, where it became clear that a full theory would have to recognize patterns of development in genes, in individual organisms, in species, and in families of species, all at once.

Paradoxically, perhaps, the appreciation of scaling phenomena must have come from the same kind of expansion of human vision that had killed the earlier naïve ideas of self-similarity. By the late twentieth century, in ways never before conceivable, images of the incomprehensibly small and the unimaginably large became part of everyone’s experience. The culture saw photographs of galaxies and of atoms. No one had to imagine, with Leibniz, what the universe might be like on microscopic or telescopic scales—microscopes and telescopes made those images part of everyday experience. Given the eagerness of the mind to find analogies in experience, new kinds of comparison between large and small were inevitable—and some of them were productive.

Often the scientists drawn to fractal geometry felt emotional parallels between their new mathematical aesthetic and changes in the arts in the second half of the century. They felt that they were drawing some inner enthusiasm from the culture at large. To Mandelbrot the epitome of the Euclidean sensibility outside mathematics was the architecture of the Bauhaus. It might just as well have been the style of painting best exemplified by the color squares of Josef Albers: spare, orderly, linear, reductionist, geometrical. Geometrical—the word means what it has meant for thousands of years. Buildings that are called geometrical are composed of simple shapes, straight lines and circles, describable with just a few numbers. The vogue for geometrical architecture and painting came and went. Architects no longer care to build blockish skyscrapers like the Seagram Building in New York, once much hailed and copied. To Mandelbrot and his followers the reason is clear. Simple shapes are inhuman. They fail to resonate with the way nature organizes itself or with the way human perception sees the world. In the words of Gert Eilenberger, a German physicist who took up nonlinear science after specializing in superconductivity: “Why is it thatthe silhouette of a storm-bent leafless tree against an evening sky in winter is perceived as beautiful, but the corresponding silhouette of any multi-purpose university building is not, in spite of all efforts of the architect? The answer seems to me, even if somewhat speculative, to follow from the new insights into dynamical systems. Our feeling for beauty is inspired by the harmonious arrangement of order and disorder as it occurs in natural objects—in clouds, trees, mountain ranges, or snow crystals. The shapes of all these are dynamical processes jelled into physical forms, and particular combinations of order and disorder are typical for them.”

A geometrical shape has a scale, a characteristic size. To Mandelbrot, art that satisfies lacks scale, in the sense that it contains important elements at all sizes. Against the Seagram Building, he offers the architecture of the Beaux-Arts, with its sculptures and gargoyles, its quoins and jamb stones, its cartouches decorated with scrollwork, its cornices topped with cheneaux and lined with dentils. A Beaux-Arts paragon like the Paris Opera has no scale because it has every scale. An observer seeing the building from any distance finds some detail that draws the eye. The composition changes as one approaches and new elements of the structure come into play.

Appreciating the harmonious structure of any architecture is one thing; admiring the wildness of nature is quite another. In terms of aesthetic values, the new mathematics of fractal geometry brought hard science in tune with the peculiarly modern feeling for untamed, uncivilized, undomesticated nature. At one time rain forests, deserts, bush, and badlands represented all that society was striving to subdue. If people wanted aesthetic satisfaction from vegetation, they looked at gardens. As John Fowles put it, writing of eighteenth-century England: “The period had no sympathy with unregulated or primordial nature. It was aggressive wilderness, an ugly and all-invasive reminder of the Fall, of man’s eternal exile from the Garden of Eden…. Even its natural sciences…remained essentially hostile to wild nature, seeing it only as something to be tamed, classified, utilised, exploited.” By the end of the twentieth century, the culture had changed, and now science was changing with it.

So science found a use after all for the obscure and fanciful cousins of the Cantor set and the Koch curve. At first, these shapes could have served as items of evidence in the divorce proceedings between mathematics and the physical sciences at the turn of the century, the end of a marriage that had been the dominating theme of science since Newton. Mathematicians like Cantor and Koch had delighted in their originality. They thought they were outsmarting nature—when actually they had not yet caught up with nature’s creation. The prestigious mainstream of physics, too, turned away from the world of everyday experience. Only later, after Steve Smale brought mathematicians back to dynamical systems, could a physicist say, “We have the astronomers and mathematicians to thank for passing the field on to us, physicists, in a much better shape than we left it to them, 70 years ago.”

Yet, despite Smale and despite Mandelbrot, it was to be the physicists after all who made a new science of chaos. Mandelbrot provided an indispensable language and a catalogue of surprising pictures of nature. As Mandelbrot himself acknowledged, his program described better than it explained. He could list elements of nature along with their fractal dimensions—seacoasts, river networks, tree bark, galaxies—and scientists could use those numbers to make predictions. But physicists wanted to know more. They wanted to know why. There were forms in nature—not visible forms, but shapes embedded in the fabric of motion—waiting to be revealed.