Chaos: Making a New Science - James Gleick (1988)
Life’s Ups and Downs
The result of a mathematical development should be continuously checked against one’s own intuition about what constitutes reasonable biological behavior. When such a check reveals disagreement, then the following possibilities must be considered:
a. A mistake has been made in the formal mathematical development;
b. The starting assumptions are incorrect and/or constitute a too drastic oversimplification;
c. One’s own intuition about the biological field is inadequately developed;
d. A penetrating new principle has been discovered.
—HARVEY J. GOLD,
Mathematical Modeling
of Biological Systems
RAVENOUS FISH AND TASTY plankton. Rain forests dripping with nameless reptiles, birds gliding under canopies of leaves, insects buzzing like electrons in an accelerator. Frost belts where voles and lemmings flourish and diminish with tidy four-year periodicity in the face of nature’s bloody combat. The world makes a messy laboratory for ecologists, a cauldron of five million interacting species. Or is it fifty million? Ecologists do not actually know.
Mathematically inclined biologists of the twentieth century built a discipline, ecology, that stripped away the noise and color of real life and treated populations as dynamical systems. Ecologists used the elementary tools of mathematical physics to describe life’s ebbs and flows. Single species multiplying in a place where food is limited, several species competing for existence, epidemics spreading through host populations—all could be isolated, if not in laboratories then certainly in the minds of biological theorists.
In the emergence of chaos as a new science in the 1970s, ecologists were destined to play a special role. They used mathematical models, but they always knew that the models were thin approximations of the seething real world. In a perverse way, their awareness of the limitations allowed them to see the importance of some ideas that mathematicians had considered interesting oddities. If regular equations could produce irregular behavior—to an ecologist, that rang certain bells. The equations applied to population biology were elementary counterparts of the models used by physicists for their pieces of the universe. Yet the complexity of the real phenomena studied in the life sciences outstripped anything to be found in a physicist’s laboratory. Biologists’ mathematical models tended to be caricatures of reality, as did the models of economists, demographers, psychologists, and urban planners, when those soft sciences tried to bring rigor to their study of systems changing over time. The standards were different. To a physicist, a system of equations like Lorenz’s was so simple it seemed virtually transparent. To a biologist, even Lorenz’s equations seemed forbiddingly complex—three-dimensional, continuously variable, and analytically intractable.
Necessity created a different style of working for biologists. The matching of mathematical descriptions to real systems had to proceed in a different direction. A physicist, looking at a particular system (say, two pendulums coupled by a spring), begins by choosing the appropriate equations. Preferably, he looks them up in a handbook; failing that, he finds the right equations from first principles. He knows how pendulums work, and he knows about springs. Then he solves the equations, if he can. A biologist, by contrast, could never simply deduce the proper equations by just thinking about a particular animal population. He would have to gather data and try to find equations that produced similar output. What happens if you put one thousand fish in a pond with a limited food supply? What happens if you add fifty sharks that like to eat two fish per day? What happens to a virus that kills at a certain rate and spreads at a certain rate depending on population density? Scientists idealized these questions so that they could apply crisp formulas.
Often it worked. Population biology learned quite a bit about the history of life, how predators interact with their prey, how a change in a country’s population density affects the spread of disease. If a certain mathematical model surged ahead, or reached equilibrium, or died out, ecologists could guess something about the circumstances in which a real population or epidemic would do the same.
One helpful simplification was to model the world in terms of discrete time intervals, like a watch hand that jerks forward second by second instead of gliding continuously. Differential equations describe processes that change smoothly over time, but differential equations are hard to compute. Simpler equations—“difference equations”—can be used for processes that jump from state to state. Fortunately, many animal populations do what they do in neat one-year intervals. Changes year to year are often more important than changes on a continuum. Unlike people, many insects, for example, stick to a single breeding season, so their generations do not overlap. To guess next spring’s gypsy moth population or next winter’s measles epidemic, an ecologist might only need to know the corresponding figure for this year. A year-by-year facsimile produces no more than a shadow of a system’s intricacies, but in many real applications the shadow gives all the information a scientist needs.
The mathematics of ecology is to the mathematics of Steve Smale what the Ten Commandments are to the Talmud: a good set of working rules, but nothing too complicated. To describe a population changing each year, a biologist uses a formalism that a high school student can follow easily. Suppose next year’s population of gypsy moths will depend entirely on this year’s population. You could imagine a table listing all the specific possibilities—31,000 gypsy moths this year means 35,000 next year, and so forth. Or you could capture the relationship between all the numbers for this year and all the numbers for next year as a rule—a function. The population (x) next year is a function (F) of the population this year: xnext = F(x). Any particular function can be drawn on a graph, instantly giving a sense of its overall shape.
In a simple model like this one, following a population through time is a matter of taking a starting figure and applying the same function again and again. To get the population for a third year, you just apply the function to the result for the second year, and so on. The whole history of the population becomes available through this process of functional iteration—a feedback loop, each year’s output serving as the next year’s input. Feedback can get out of hand, as it does when sound from a loudspeaker feeds back through a microphone and is rapidly amplified to an unbearable shriek. Or feedback can produce stability, as a thermostat does in regulating the temperature of a house: any temperature above a fixed point leads to cooling, and any temperature below it leads to heating.
Many different types of functions are possible. A naive approach to population biology might suggest a function that increases the population by a certain percentage each year. That would be a linear function—xnext = rx—and it would be the classic Malthusian scheme for population growth, unlimited by food supply or moral restraint. The parameter r represents the rate of population growth. Say it is 1.1; then if this year’s population is 10, next year’s is 11. If the input is 20,000, the output is 22,000. The population rises higher and higher, like money left forever in a compound-interest savings account.
Ecologists realized generations ago that they would have to do better. An ecologist imagining real fish in a real pond had to find a function that matched the crude realities of life—for example, the reality of hunger, or competition. When the fish proliferate, they start to run out of food. A small fish population will grow rapidly. An overly large fish population will dwindle. Or take Japanese beetles. Every August 1 you go out to your garden and count the beetles. For simplicity’s sake, you ignore birds, ignore beetle diseases, and consider only the fixed food supply. A few beetles will multiply; many will eat the whole garden and starve themselves.
In the Malthusian scenario of unrestrained growth, the linear growth function rises forever upward. For a more realistic scenario, an ecologist needs an equation with some extra term that restrains growth when the population becomes large. The most natural function to choose would rise steeply when the population is small, reduce growth to near zero at intermediate values, and crash downward when the population is very large. By repeating the process, an ecologist can watch a population settle into its long-term behavior—presumably reaching some steady state. A successful foray into mathematics for an ecologist would let him say something like this: Here’s an equation; here’s a variable representing reproductive rate; here’s a variable representing the natural death rate; here’s a variable representing the additional death rate from starvation or predation; and look—the population will rise at this speed until it reaches that level of equilibrium.
How do you find such a function? Many different equations might work, and possibly the simplest is a modification of the linear, Malthusian version: xnext = rx(1 - x). Again, the parameter r represents a rate of growth that can be set higher or lower. The new term, 1 -x, keeps the growth within bounds, since as x rises, 1 - x falls.* Anyone with a calculator could pick some starting value, pick some growth rate, and carry out the arithmetic to derive next year’s population.
By the 1950s several ecologists were looking at variations of that particular equation, known as the logistic difference equation. In Australia, for example, W. E. Ricker applied it to real fisheries. Ecologists understood that the growth-rate parameter r represented an important feature of the model. In the physical systems from which these equations were borrowed, that parameter corresponded to the amount of heating, or the amount of friction, or the amount of some other messy quantity. In short, the amount of nonlinearity. In a pond, it might correspond to the fecundity of the fish, the propensity of the population not just to boom but also to bust (“biotic potential” was the dignified term). The question was, how did these different parameters affect the ultimate destiny of a changing population? The obvious answer is that a lower parameter will cause this idealized population to end up at a lower level. A higher parameter will lead to a higher steady state. This turns out to be correct for many parameters—but not all. Occasionally, researchers like Ricker surely tried parameters that were even higher, and when they did, they must have seen chaos.
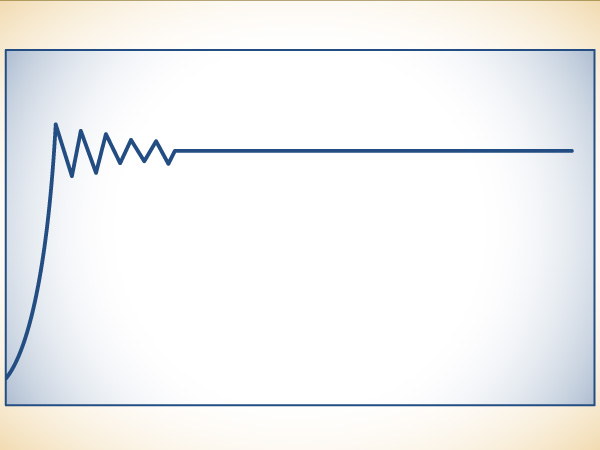
A population reaches equilibrium after rising, overshooting, and falling back.
Oddly, the flow of numbers begins to misbehave, quite a nuisance for anyone calculating with a hand crank. The numbers still do not grow without limit, of course, but they do not converge to a steady level, either. Apparently, though, none of these early ecologists had the inclination or the strength to keep churning out numbers that refused to settle down. Anyway, if the population kept bouncing back and forth, ecologists assumed that it was oscillating around some underlying equilibrium. The equilibrium was the important thing. It did not occur to the ecologists that there might be no equilibrium.
Reference books and textbooks that dealt with the logistic equation and its more complicated cousins generally did not even acknowledge that chaotic behavior could be expected. J. Maynard Smith, in the classic 1968 Mathematical Ideas in Biology, gave a standard sense of the possibilities: populations often remain approximately constant or else fluctuate “with a rather regular periodicity” around a presumed equilibrium point. It wasn’t that he was so naive as to imagine that real populations could never behave erratically. He simply assumed that erratic behavior had nothing to do with the sort of mathematical models he was describing. In any case, biologists had to keep these models at arm’s length. If the models started to betray their makers’ knowledge of the real population’s behavior, some missing feature could always explain the discrepancy: the distribution of ages in the population, some consideration of territory or geography, or the complication of having to count two sexes.
Most important, in the back of ecologists’ minds was always the assumption that an erratic string of numbers probably meant that the calculator was acting up, or just lacked accuracy. The stable solutions were the interesting ones. Order was its own reward. This business of finding appropriate equations and working out the computation was hard, after all. No one wanted to waste time on a line of work that was going awry, producing no stability. And no good ecologist ever forgot that his equations were vastly oversimplified versions of the real phenomena. The whole point of oversimplifying was to model regularity. Why go to all that trouble just to see chaos?
LATER, PEOPLE WOULD SAY that James Yorke had discovered Lorenz and given the science of chaos its name. The second part was actually true.
Yorke was a mathematician who liked to think of himself as a philosopher, though this was professionally dangerous to admit. He was brilliant and soft-spoken, a mildly disheveled admirer of the mildly disheveled Steve Smale. Like everyone else, he found Smale hard to fathom. But unlike most people, he understood why Smale was hard to fathom. When he was just twenty-two years old, Yorke joined an interdisciplinary institute at the University of Maryland called the Institute for Physical Science and Technology, which he later headed. He was the kind of mathematician who felt compelled to put his ideas of reality to some use. He produced a report on how gonorrhea spreads that persuaded the federal government to alter its national strategies for controlling the disease. He gave official testimony to the State of Maryland during the 1970s gasoline crisis, arguing correctly (but unpersuasively) that the even-odd system of limiting gasoline sales would only make lines longer. In the era of antiwar demonstrations, when the government released a spy-plane photograph purporting to show sparse crowds around the Washington Monument at the height of a rally, he analyzed the monument’s shadow to prove that the photograph had actually been taken a half-hour later, when the rally was breaking up.
At the institute, Yorke enjoyed an unusual freedom to work on problems outside traditional domains, and he enjoyed frequent contact with experts in a wide range of disciplines. One of these experts, a fluid dynamicist, had come across Lorenz’s 1963 paper “Deterministic Nonperiodic Flow” in 1972 and had fallen in love with it, handing out copies to anyone who would take one. He handed one to Yorke.
Lorenz’s paper was a piece of magic that Yorke had been looking for without even knowing it. It was a mathematical shock, to begin with—a chaotic system that violated Smale’s original optimistic classification scheme. But it was not just mathematics; it was a vivid physical model, a picture of a fluid in motion, and Yorke knew instantly that it was a thing he wanted physicists to see. Smale had steered mathematics in the direction of such physical problems, but, as Yorke well understood, the language of mathematics remained a serious barrier to communication. If only the academic world had room for hybrid mathematician/physicists—but it did not. Even though Smale’s work on dynamical systems had begun to close the gap, mathematicians continued to speak one language, physicists another. As the physicist Murray Gell-Mann once remarked: “Faculty members are familiar with a certain kind of person who looks to the mathematicians like a good physicist and looks to the physicists like a good mathematician. Very properly, they do not want that kind of person around.” The standards of the two professions were different. Mathematicians proved theorems by ratiocination; physicists’ proofs used heavier equipment. The objects that made up their worlds were different. Their examples were different.
Smale could be happy with an example like this: take a number, a fraction between zero and one, and double it. Then drop the integer part, the part to the left of the decimal point. Then repeat the process. Since most numbers are irrational and unpredictable in their fine detail, the process will just produce an unpredictable sequence of numbers. A physicist would see nothing there but a trite mathematical oddity, utterly meaningless, too simple and too abstract to be of use. Smale, though, knew intuitively that this mathematical trick would appear in the essence of many physical systems.
To a physicist, a legitimate example was a differential equation that could be written down in simple form. When Yorke saw Lorenz’s paper, even though it was buried in a meteorology journal, he knew it was an example that physicists would understand. He gave a copy to Smale, with his address label pasted on so that Smale would return it. Smale was amazed to see that this meteorologist—ten years earlier—had discovered a kind of chaos that Smale himself had once considered mathematically impossible. He made many photocopies of “Deterministic Nonperiodic Flow,” and thus arose the legend that Yorke had discovered Lorenz. Every copy of the paper that ever appeared in Berkeley had Yorke’s address label on it.
Yorke felt that physicists had learned not to see chaos. In daily life, the Lorenzian quality of sensitive dependence on initial conditions lurks everywhere. A man leaves the house in the morning thirty seconds late, a flowerpot misses his head by a few millimeters, and then he is run over by a truck. Or, less dramatically, he misses a bus that runs every ten minutes—his connection to a train that runs every hour. Small perturbations in one’s daily trajectory can have large consequences. A batter facing a pitched ball knows that approximately the same swing will not give approximately the same result, baseball being a game of inches. Science, though—science was different.
Pedagogically speaking, a good share of physics and mathematics was—and is—writing differential equations on a blackboard and showing students how to solve them. Differential equations represent reality as a continuum, changing smoothly from place to place and from time to time, not broken in discrete grid points or time steps. As every science student knows, solving differential equations is hard. But in two and a half centuries, scientists have built up a tremendous body of knowledge about them: handbooks and catalogues of differential equations, along with various methods for solving them, or “finding a closed-form integral,” as a scientist will say. It is no exaggeration to say that the vast business of calculus made possible most of the practical triumphs of post-medieval science; nor to say that it stands as one of the most ingenious creations of humans trying to model the changeable world around them. So by the time a scientist masters this way of thinking about nature, becoming comfortable with the theory and the hard, hard practice, he is likely to have lost sight of one fact. Most differential equations cannot be solved at all.
“If you could write down the solution to a differential equation,” Yorke said, “then necessarily it’s not chaotic, because to write it down, you must find regular invariants, things that are conserved, like angular momentum. You find enough of these things, and that lets you write down a solution. But this is exactly the way to eliminate the possibility of chaos.”
The solvable systems are the ones shown in textbooks. They behave. Confronted with a nonlinear system, scientists would have to substitute linear approximations or find some other uncertain backdoor approach. Textbooks showed students only the rare nonlinear systems that would give way to such techniques. They did not display sensitive dependence on initial conditions. Nonlinear systems with real chaos were rarely taught and rarely learned. When people stumbled across such things—and people did—all their training argued for dismissing them as aberrations. Only a few were able to remember that the solvable, orderly, linear systems were the aberrations. Only a few, that is, understood how nonlinear nature is in its soul. Enrico Fermi once exclaimed, “It does not say in the Bible that all laws of nature are expressible linearly!” The mathematician Stanislaw Ulam remarked that to call the study of chaos “nonlinear science” was like calling zoology “the study of non elephant animals.”
Yorke understood. “The first message is that there is disorder. Physicists and mathematicians want to discover regularities. People say, what use is disorder. But people have to know about disorder if they are going to deal with it. The auto mechanic who doesn’t know about sludge in valves is not a good mechanic.” Scientists and nonscientists alike, Yorke believed, can easily mislead themselves about complexity if they are not properly attuned to it. Why do investors insist on the existence of cycles in gold and silver prices? Because periodicity is the most complicated orderly behavior they can imagine. When they see a complicated pattern of prices, they look for some periodicity wrapped in a little random noise. And scientific experimenters, in physics or chemistry or biology, are no different. “In the past, people have seen chaotic behavior in innumerable circumstances,” Yorke said. “They’re running a physical experiment, and the experiment behaves in an erratic manner. They try to fix it or they give up. They explain the erratic behavior by saying there’s noise, or just that the experiment is bad.”
Yorke decided there was a message in the work of Lorenz and Smale that physicists were not hearing. So he wrote a paper for the most broadly distributed journal he thought he could publish in, the American Mathematical Monthly. (As a mathematician, he found himself helpless to phrase ideas in a form that physics journals would find acceptable; it was only years later that he hit upon the trick of collaborating with physicists.) Yorke’s paper was important on its merits, but in the end its most influential feature was its mysterious and mischievous title: “Period Three Implies Chaos.” His colleagues advised him to choose something more sober, but Yorke stuck with a word that came to stand for the whole growing business of deterministic disorder. He also talked to his friend Robert May, a biologist.
MAY CAME TO BIOLOGY through the back door, as it happened. He started as a theoretical physicist in his native Sydney, Australia, the son of a brilliant barrister, and he did postdoctoral work in applied mathematics at Harvard. In 1971, he went for a year to the Institute for Advanced Study in Princeton; instead of doing the work he was supposed to be doing, he found himself drifting over to Princeton University to talk to the biologists there.
Even now, biologists tend not to have much mathematics beyond calculus. People who like mathematics and have an aptitude for it tend more toward mathematics or physics than the life sciences. May was an exception. His interests at first tended toward the abstract problems of stability and complexity, mathematical explanations of what enables competitors to coexist. But he soon began to focus on the simplest ecological questions of how single populations behave over time. The inevitably simple models seemed less of a compromise. By the time he joined the Princeton faculty for good—eventually he would become the university’s dean for research—he had already spent many hours studying a version of the logistic difference equation, using mathematical analysis and also a primitive hand calculator.
Once, in fact, on a corridor blackboard back in Sydney, he wrote the equation out as a problem for the graduate students. It was starting to annoy him. “What the Christ happens when lambda gets bigger than the point of accumulation?” What happened, that is, when a population’s rate of growth, its tendency toward boom and bust, passed a critical point. By trying different values of this nonlinear parameter, May found that he could dramatically change the system’s character. Raising the parameter meant raising the degree of nonlinearity, and that changed not just the quantity of the outcome, but also its quality. It affected not just the final population at equilibrium, but also whether the population would reach equilibrium at all.
When the parameter was low, May’s simple model settled on a steady state. When the parameter was high, the steady state would break apart, and the population would oscillate between two alternating values. When the parameter was very high, the system—the very same system—seemed to behave unpredictably. Why? What exactly happened at the boundaries between the different kinds of behavior? May couldn’t figure it out. (Nor could the graduate students.)
May carried out a program of intense numerical exploration into the behavior of this simplest of equations. His program was analogous to Smale’s: he was trying to understand this one simple equation all at once, not locally but globally. The equation was far simpler than anything Smale had studied. It seemed incredible that its possibilities for creating order and disorder had not been exhausted long since. But they had not. Indeed, May’s program was just a beginning. He investigated hundreds of different values of the parameter, setting the feedback loop in motion and watching to see where—and whether—the string of numbers would settle down to a fixed point. He focused more and more closely on the critical boundary between steadiness and oscillation. It was as if he had his own fish pond, where he could wield fine mastery over the “boom-and-bustiness” of the fish. Still using the logistic equation, xnext = rx(1-x), May increased the parameter as slowly as he could. If the parameter was 2.7, then the population would be .6292. As the parameter rose, the final population rose slightly, too, making a line that rose slightly as it moved from left to right on the graph.
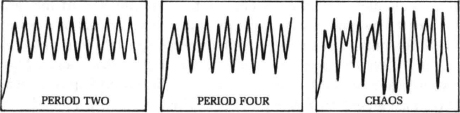
Suddenly, though, as the parameter passed 3, the line broke in two. May’s imaginary fish population refused to settle down to a single value, but oscillated between two points in alternating years. Starting at a low number, the population would rise and then fluctuate until it was steadily flipping back and forth. Turning up the knob a bit more—raising the parameter a bit more—would split the oscillation again, producing a string of numbers that settled down to four different values, each returning every fourth year.* Now the population rose and fell on a regular four-year schedule. The cycle had doubled again—first from yearly to every two years, and now to four. Once again, the resulting cyclical behavior was stable; different starting values for the population would converge on the same four-year cycle.
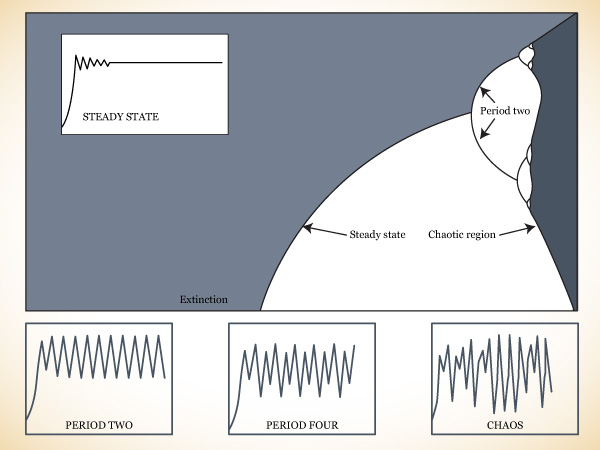
PERIOD-DOUBLINGS AND CHAOS. Instead of using individual diagrams to show the behavior of populations with different degrees of fertility, Robert May and other scientists used a “bifurcation diagram” to assemble all the information into a single picture.
The diagram shows how changes in one parameter—in this case, a wildlife population’s “boom-and-bustiness”—would change the ultimate behavior of this simple system. Values of the parameter are represented from left to right; the final population is plotted on the vertical axis. In a sense, turning up the parameter value means driving a system harder, increasing its nonlinearity.
Where the parameter is low (left), the population becomes extinct. As the parameter rises (center), so does the equilibrium level of the population. Then, as the parameter rises further, the equilibrium splits in two, just as turning up the heat in a convecting fluid causes an instability to set in; the population begins to alternate between two different levels. The splittings, or bifurcations, come faster and faster. Then the system turns chaotic (right), and the population visits infinitely many different values.
As Lorenz had discovered a decade before, the only way to make sense of such numbers and preserve one’s eyesight is to create a graph. May drew a sketchy outline meant to sum up all the knowledge about the behavior of such a system at different parameters. The level of the parameter was plotted horizontally, increasing from left to right. The population was represented vertically. For each parameter, May plotted a point representing the final outcome, after the system reached equilibrium. At the left, where the parameter was low, this outcome would just be a point, so different parameters produced a line rising slightly from left to right. When the parameter passed the first critical point, May would have to plot two populations: the line would split in two, making a sideways Y or a pitchfork. This split corresponded to a population going from a one-year cycle to a two-year cycle.
As the parameter rose further, the number of points doubled again, then again, then again. It was dumbfounding—such complex behavior, and yet so tantalizingly regular. “The snake in the mathematical grass” was how May put it. The doublings themselves were bifurcations, and each bifurcation meant that the pattern of repetition was breaking down a step further. A population that had been stable would alternate between different levels every other year. A population that had been alternating on a two-year cycle would now vary on the third and fourth years, thus switching to period four.
These bifurcations would come faster and faster—4, 8, 16, 32…—and suddenly break off. Beyond a certain point, the “point of accumulation,” periodicity gives way to chaos, fluctuations that never settle down at all. Whole regions of the graph are completely blacked in. If you were following an animal population governed by this simplest of nonlinear equations, you would think the changes from year to year were absolutely random, as though blown about by environmental noise. Yet in the middle of this complexity, stable cycles suddenly return. Even though the parameter is rising, meaning that the nonlinearity is driving the system harder and harder, a window will suddenly appear with a regular period: an odd period, like 3 or 7. The pattern of changing population repeats itself on a three-year or seven-year cycle. Then the period-doubling bifurcations begin all over at a faster rate, rapidly passing through cycles of 3, 6, 12…or 7, 14, 28…, and then breaking off once again to renewed chaos.
At first, May could not see this whole picture. But the fragments he could calculate were unsettling enough. In a real-world system, an observer would see just the vertical slice corresponding to one parameter at a time. He would see only one kind of behavior—possibly a steady state, possibly a seven-year cycle, possibly apparent randomness. He would have no way of knowing that the same system, with some slight change in some parameter, could display patterns of a completely different kind.
James Yorke analyzed this behavior with mathematical rigor in his “Period Three Implies Chaos” paper. He proved that in any one-dimensional system, if a regular cycle of period three ever appears, then the same system will also display regular cycles of every other length, as well as completely chaotic cycles. This was the discovery that came as an “electric shock” to physicists like Freeman Dyson. It was so contrary to intuition. You would think it would be trivial to set up a system that would repeat itself in a period-three oscillation without ever producing chaos. Yorke showed that it was impossible.
Startling though it was, Yorke believed that the public relations value of his paper outweighed the mathematical substance. That was partly true. A few years later, attending an international conference in East Berlin, he took some time out for sightseeing and went for a boat ride on the Spree. Suddenly he was approached by a Russian trying urgently to communicate something. With the help of a Polish friend, Yorke finally understood that the Russian was claiming to have proved the same result. The Russian refused to give details, saying only that he would send his paper. Four months later it arrived. A. N. Sarkovskiihad indeed been there first, in a paper titled “Coexistence of Cycles of a Continuous Map of a Line into Itself.” But Yorke had offered more than a mathematical result. He had sent a message to physicists: Chaos is ubiquitous; it is stable; it is structured. He also gave reason to believe that complicated systems, traditionally modeled by hard continuous differential equations, could be understood in terms of easy discrete maps.
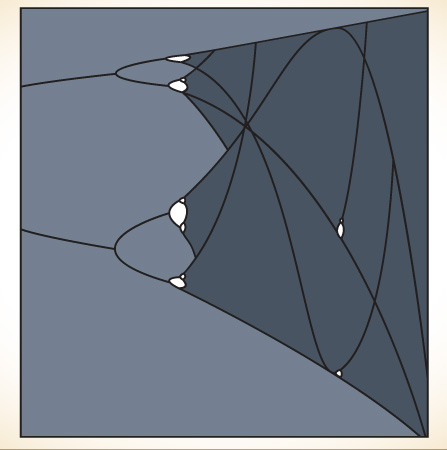
WINDOWS OF ORDER INSIDE CHAOS. Even with the simplest equation, the region of chaos in a bifurcation diagram proves to have an intricate structure—far more orderly than Robert May could guess at first. First, the bifurcations produce periods of 2, 4, 8, 16…. Then chaos begins, with no regular periods. But then, as the system is driven harder, windows appear with odd periods. A stable period 3 appears, and then the period-doubling begins again 6, 12, 24…. The structure is infinitely deep. When portions are magnified, they turn out to resemble the whole diagram.
The sightseeing encounter between these frustrated, gesticulating mathematicians was a symptom of a continuing communications gap between Soviet and Western science. Partly because of language, partly because of restricted travel on the Soviet side, sophisticated Western scientists have often repeated work that already existed in the Soviet literature. The blossoming of chaos in the United States and Europe has inspired a huge body of parallel work in the Soviet Union; on the other hand, it also inspired considerable bewilderment, because much of the new science was not so new in Moscow. Soviet mathematicians and physicists had a strong tradition in chaos research, dating back to the work of A. N. Kolmogorov in the fifties. Furthermore, they had a tradition of working together that had survived the divergence of mathematics and physics elsewhere.
Thus Soviet scientists were receptive to Smale—his horseshoe created a considerable stir in the sixties. A brilliant mathematical physicist, Yasha Sinai, quickly translated similar systems into thermodynamic terms. Similarly, when Lorenz’s work finally reached Western physics in the seventies, it simultaneously spread in the Soviet Union. And in 1975, as Yorke and May struggled to capture the attention of their colleagues, Sinai and others rapidly assembled a powerful working group of physicists centered in Gorki. In recent years, some Western chaos experts have made a point of traveling regularly to the Soviet Union to stay current; most, however, have had to content themselves with the Western version of their science.
In the West, Yorke and May were the first to feel the full shock of period-doubling and to pass the shock along to the community of scientists. The few mathematicians who had noted the phenomenon treated it as a technical matter, a numerical oddity: almost a kind of game playing. Not that they considered it trivial. But they considered it a thing of their special universe.
Biologists had overlooked bifurcations on the way to chaos because they lacked mathematical sophistication and because they lacked the motivation to explore disorderly behavior. Mathematicians had seen bifurcations but had moved on. May, a man with one foot in each world, understood that he was entering a domain that was astonishing and profound.
TO SEE DEEPER INTO this simplest of systems, scientists needed greater computing power. Frank Hoppensteadt, at New York University’s Courant Institute of Mathematical Sciences, had so powerful a computer that he decided to make a movie.
Hoppensteadt, a mathematician who later developed a strong interest in biological problems, fed the logistic nonlinear equation through his Control Data 6600 hundreds of millions of times. He took pictures from the computer’s display screen at each of a thousand different values of the parameter, a thousand different tunings. The bifurcations appeared, then chaos—and then, within the chaos, the little spikes of order, ephemeral in their instability. Fleeting bits of periodic behavior. Staring at his own film, Hoppensteadt felt as if he were flying through an alien landscape. One instant it wouldn’t look chaotic at all. The next instant it would be filled with unpredictable tumult. The feeling of astonishment was something Hoppensteadt never got over.
May saw Hoppensteadt’s movie. He also began collecting analogues from other fields, such as genetics, economics, and fluid dynamics. As a town crier for chaos, he had two advantages over the pure mathematicians. One was that, for him, the simple equations could not represent reality perfectly. He knew they were just metaphors—so he began to wonder how widely the metaphors could apply. The other was that the revelations of chaos fed directly into a vehement controversy in his chosen field.
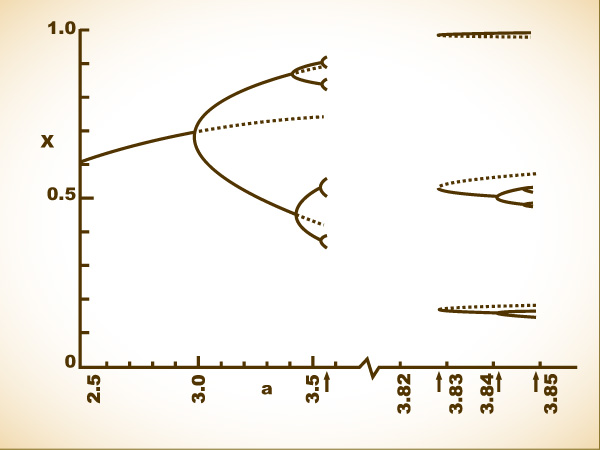
The outline of the bifurcation diagram as May first saw it, before more powerful computation revealed its rich structure.
Population biology had long been a magnet for controversy anyway. There was tension in biology departments, for example, between molecular biologists and ecologists. The molecular biologists thought that they did real science, crisp, hard problems, whereas the work of ecologists was vague. Ecologists believed that the technical masterpieces of molecular biology were just clever elaborations of well-defined problems.
Within ecology itself, as May saw it, a central controversy in the early 1970s dealt with the nature of population change. Ecologists were divided almost along lines of personality. Some read the message of the world to be orderly: populations are regulated and steady—with exceptions. Others read the opposite message: populations fluctuate erratically—with exceptions. By no coincidence, these opposing camps also divided over the application of hard mathematics to messy biological questions. Those who believed that populations were steady argued that they must be regulated by some deterministic mechanisms. Those who believed that populations were erratic argued that they must be bounced around by unpredictable environmental factors, wiping out whatever deterministic signal might exist. Either deterministic mathematics produced steady behavior, or random external noise produced random behavior. That was the choice.
In the context of that debate, chaos brought an astonishing message: simple deterministic models could produce what looked like random behavior. The behavior actually had an exquisite fine structure, yet any piece of it seemed indistinguishable from noise. The discovery cut through the heart of the controversy.
As May looked at more and more biological systems through the prism of simple chaotic models, he continued to see results that violated the standard intuition of practitioners. In epidemiology, for example, it was well known that epidemics tend to come in cycles, regular or irregular. Measles, polio, rubella—all rise and fall in frequency. May realized that the oscillations could be reproduced by a nonlinear model and he wondered what would happen if such a system received a sudden kick—a perturbation of the kind that might correspond to a program of inoculation. Naïve intuition suggests that the system will change smoothly in the desired direction. But actually, May found, huge oscillations are likely to begin. Even if the long-term trend was turned solidly downward, the path to a new equilibrium would be interrupted by surprising peaks. In fact, in data from real programs, such as a campaign to wipe out rubella in Britain, doctors had seen oscillations just like those predicted by May’s model. Yet any health official, seeing a sharp short-term rise in rubella or gonorrhea, would assume that the inoculation program had failed.
Within a few years, the study of chaos gave a strong impetus to theoretical biology, bringing biologists and physicists into scholarly partnerships that were inconceivable a few years before. Ecologists and epidemiologists dug out old data that earlier scientists had discarded as too unwieldy to handle. Deterministic chaos was found in records of New York City measles epidemics and in two hundred years of fluctuations of the Canadian lynx population, as recorded by the trappers of the Hudson’s Bay Company. Molecular biologists began to see proteins as systems in motion. Physiologists looked at organs not as static structures but as complexes of oscillations, some regular and some irregular.
All through science, May knew, specialists had seen and argued about the complex behavior of systems. Each discipline considered its particular brand of chaos to be special unto itself. The thought inspired despair. Yet what if apparent randomness could come from simple models? And what if the same simple models applied to complexity in different fields? May realized that the astonishing structures he had barely begun to explore had no intrinsic connection to biology. He wondered how many other sorts of scientists would be as astonished as he. He set to work on what he eventually thought of as his “messianic” paper, a review article in 1976 for Nature.
The world would be a better place, May argued, if every young student were given a pocket calculator and encouraged to play with the logistic difference equation. That simple calculation, which he laid out in fine detail in the Nature article, could counter the distorted sense of the world’s possibilities that comes from a standard scientific education. It would change the way people thought about everything from the theory of business cycles to the propagation of rumors.
Chaos should be taught, he argued. It was time to recognize that the standard education of a scientist gave the wrong impression. No matter how elaborate linear mathematics could get, with its Fourier transforms, its orthogonal functions, its regression techniques, May argued that it inevitably misled scientists about their overwhelmingly nonlinear world. “The mathematical intuition so developed ill equips the student to confront the bizarre behaviour exhibited by the simplest of discrete nonlinear systems,” he wrote.
“Not only in research, but also in the everyday world of politics and economics, we would all be better off if more people realized that simple nonlinear systems do not necessarily possess simple dynamical properties.”
______________
* For convenience, in this highly abstract model, “population” is expressed as a fraction between zero and one, zero representing extinction, one representing the greatest conceivable population of the pond.
So begin: Choose an arbitrary value for r, say, 2.7, and a starting population of .02. One minus .02 is .98. Multiply by 0.02 and you get .0196. Multiply that by 2.7 and you get .0529. The very small starting population has more than doubled. Repeat the process, using the new population as the seed, and you get .1353. With a cheap programmable calculator, this iteration is just a matter of pushing one button over and over again. The population rises to .3159, then .5835, then .6562—the rate of increase is slowing. Then, as starvation overtakes reproduction, .6092. Then .6428, then .6199, then .6362, then .6249. The numbers seem to be bouncing back and forth, but closing in on a fixed number: .6328, .6273, .6312, .6285, .6304, .6291, .6300, .6294, .6299, .6295, .6297, .6296, .6297, .6296, .6296, .6296, .6296, .6296, .6296, .6296. Success!
In the days of pencil-and-paper arithmetic, and in the days of mechanical adding machines with hand cranks, numerical exploration never went much further.
* With a parameter of 3.5, say, and a starting value of .4, he would see a string of numbers like this:
.4000, .8400, .4704, .8719,
.3908, .8332, .4862, .8743,
.3846, .8284, .4976, .8750,
.3829, .8270, .4976, .8750,
.3829, .8270, .5008, .8750,
.3828, .8269, .5009, .8750,
.3828, .8269, .5009, .8750, etc.