Bad Astronomy: Misconceptions and Misuses Revealed, from Astrology to the Moon Landing “Hoax” - Philip Plait (2002)

Part II. From the Earth to the Moon

Chapter 7. The Gravity of the Situation: The Moon and the Tides

"There is a tide in the affairs of men ... "

-Julius Caesar by William Shakespeare

f I had a nickel for every time I am asked about tides … I'd have a lot of nickels.

There are a lot of misconceptions about tides. Anyone who has spent a day at the beach knows about tides; the difference between high and low tide can be substantial. But the details of tides can be a bit weird. For example, there are roughly two high tides and two low tides a day. I get questions about this all the time. Most people have heard that the Moon's gravity causes tides, so why are there two high tides each day? Shouldn't there be only one high tide, when the Moon is overhead, with a low tide on the opposite side of the Earth?

When I wrote a web page about tides, and again while researching them for this chapter, I couldn't find a single source that made any sense. Different web pages and different books all had different explanations. Some made sense for a while, then said something clearly wrong. Others started off wrong and got worse from there. Most are close, showing that the explanation relies on several different factors. What's worse: I wrote a draft of this chapter and even had it submitted for the book, then realized what I said was essentially wrong! What you'll read here is now correct. It's funny, too-even people who get tides right rarely take the discussion far enough. Tides have far-reaching consequences, from locking together the Moon's spin and orbital motion to the volcanoes on Jupiter's moon Io. Tidal forces can even cause entire galaxies to be ripped apart, torn to shreds by even bigger galaxies.

When astronomers talk about tides, we usually don't mean the actual movement of water. We are using the term as a shorthand for the tidal force. This is a force much like gravity, and in fact is related to gravity. We're all aware of gravity from the first time we try to stand up and walk. As we age, we become increasingly aware of it. For me, it seems harder to get out of bed every day, and easier to drop things. Sometimes I wonder if the Earth is pulling harder on me each day.

It doesn't really, of course. Gravity doesn't change with time. The force of gravity, the amount that it pulls on an object, depends on only two things: the mass of the object doing the pulling, and how far away it is.

Anything with mass has gravity. You do, I do, planets do, a feather does. I can exact a minute amount of revenge on Earth's gravity knowing that I am pulling back on the Earth as well. The amount I am pulling is pretty small, sure, but it's there. The more massive the object, the more it pulls. The Earth has a lot more mass than I do (something like 78,000,000,000,000,000,000,000 times as much, but who's counting?), so it pulls on me a lot harder than I do on it.

If I were to get farther away from the Earth, that force would weaken. As a matter of fact, the force drops with the square of my distance; that is, if I double my distance, the force drops by a factor of 2 X 2 = 4. If I triple my distance, it drops by 3 X 3 = 9, and so on.

That does not mean that I feel one-quarter of the gravity if I climb a ladder to twice my height, though! We don't measure distance from the surface of the Earth, we measure it from its center. A few hundred years ago, Sir Isaac Newton, the seventeenth-century philosopher-scientist, showed mathematically that as far as distance is concerned, you can imagine that all the mass of the Earth is condensed into a tiny point at its center, so it's from there that we measure distance.

The Earth's radius is about 6,400 kilometers (4,000 miles), so for me to double my distance, I'd have to book a flight on a rocket: I'd need to get an additional 6,400 kilometers off the ground, nearly one-sixtieth of the way to the Moon. Only there would I feel like I weigh a quarter of what I do now. It seems like a rather drastic way to lose weight.

Because the Moon is smaller and less massive than the Earth, you would feel a gravity about one-sixth that of the Earth's if you were standing on the lunar surface. That's still a substantial pull. Of course, the Moon is pretty far away, so its gravitational effect here on Earth is much smaller. It orbits the Earth at an average distance of about 384,000 kilometers (240,000 miles). From that distance its gravity drops by a factor of nearly 50,000, so we can't feel it.

But it's there. Gravity never goes away completely. Although on the Earth the force of gravity from the Moon is terribly weak, it still extends its invisible hand, grasping our planet, pulling on it.

That grasp weakens with distance, giving rise to an interesting effect on the Earth. The part of Earth nearest the Moon feels a stronger pull than the part of the Earth farthest from the Moon. The difference in distance-the diameter of the Earth-means a difference in gravity. The near side of the Earth feels a pull about 6 percent stronger than the far side. This difference in pull tends to stretch the Earth a little bit. It's because the gravity is different from one side of the Earth to the other, so we call it differential gravity.

Gravity always attracts, so the force of lunar gravity is always a pull toward the Moon. So, you would think, since the near side of the Earth feels a stronger pull, water would pile up there, giving us a high tide. On the far side of the Earth there should be a low tide, a flattening, perhaps, because even though the force is weaker, it still points toward the Moon.

But we know that's not right. There are two high and two low tides a day. That means at any one time there must be a high tide on the opposite side of the Earth from the Moon as well. How can this be?

Clearly, differential gravity isn't enough to explain tides. For the complete picture, we have to look once again to the Moon.

Allow me to digress for a moment.

A couple of years ago, my two good friends Ben and Nicky got married. They asked my then-three-year-old daughter Zoe to be the flower girl. The ceremony was lovely, and afterwards at the reception we all danced. Zoe wanted to dance with me, and what proud father could say no?

So I took her hands and we danced in a circle. I had to lean backwards a little to make sure we didn't topple over, and as I swung her around I couldn't help noticing that the circle she made on the floor was big, and the one I made was small. Since my mass was about five times what hers was, she made a circle five times bigger than mine.

So what does this have to do with tides? Everything. Our little dance is a tiny version of the same tango in which the Earth and Moon participate. Instead of holding each other's hands, the Earth and Moon use gravity to embrace. And just like Zoe and me, they both make circles.

Since the Moon's mass is one-eightieth the mass of the Earth, the effect of the Moon's pull on the Earth is one-eightieth the effect of the Earth's pull on the moon. Like my daughter making a bigger circle on the dance floor than I did, the Moon makes a big circle around the Earth, but the Earth also makes a little circle at the same time.

This means that the Moon and the Earth are actually orbiting a point in between the two bodies, as if all the mass in the EarthMoon system is concentrated there. This point is called the center of mass, or technically the barycenter. Since the Earth is about 80 times the mass of the Moon, the center of mass of the whole system is about one-eightieth of the way from the center of the Earth to the center of the Moon. That's about 4,800 kilometers (3,000 miles) or so from the center of the Earth, or about 1,600 kilometers (1,000 miles) beneath the Earth's surface. If you could watch the Earth from outer space, you'd see it make a little circle centered on a point 1,600 kilometers beneath its surface, once every month. In a very real sense, the center of mass of the Earth (which is basically the center of the Earth itself) is orbiting the center of mass of the Earth-Moon system, making that little circle once a month.

This has some interesting implications. To see this, think about the astronauts on board the space station. They float freely, as if there is no gravity. In fact, they feel gravity almost as strongly as we do here on the surface of the Earth; after all, they are only a few hundred kilometers high, not much compared to the 6,400- kilometer radius of the Earth. The astronauts float because they are in free fall; the Earth is pulling them down, so they fall. But they have so much sideways velocity that they basically keep missing the Earth. Their orbit carries them along a curve that has the same curvature of the Earth, so they continuously fall but never get any closer to the ground.

An astronaut standing on a scale in the space station would measure her weight as zero because she is falling around the center of the Earth. Gravity affects her, but she cannot feel it. This is always true for an orbiting object.

But remember, the center of the Earth is orbiting the EarthMoon barycenter, too. So even though the center of the Earth is affected by gravity from the Moon, someone standing there would not actually feel that force. They would be in free fall!

But someone standing under the Moon on the Earth's surface would feel the Moon's pull. Someone standing on the opposite side would, too, but more weakly. But since the force felt from the Moon's gravity is zero at the Earth's center, we can measure the Moon's gravity relative to the center of the Earth. To someone on the side of the Earth nearest the Moon, there would be a force felt toward the Moon. Someone in the center of the Earth feels no force (remember, they are in free fall). But the person on the far side of the Earth feels less force toward the Moon than the person at the center of the Earth. But what's smaller than zero force? A negative force; in other words, a positive force in the other direction, away from the Moon.

It seems paradoxical that gravity can act in such a way as to make something feel a force away from an object, but in this case it's because we are measuring that force relative to the center of the Earth. When you do that, then you do indeed get a force pointing away from the Moon on the far side of the Earth.

That is why we have two high tides. There is a net force toward the Moon on the near side, and a net force away from the Moon on the far side. The water follows those forces, piling up in a high tide on opposite sides of the Earth. In between the two high tides are the low tides, and of course there are two of them as well. As a point on the Earth rotates under the high tide bulge, the water rises. A few hours later, when the Earth has rotated onequarter of the way around, that point is now under a low tide, and the water has receded. One-quarter of the way around again and you've got a high tide. On and on it goes, with high and low tides alternating roughly every six hours.

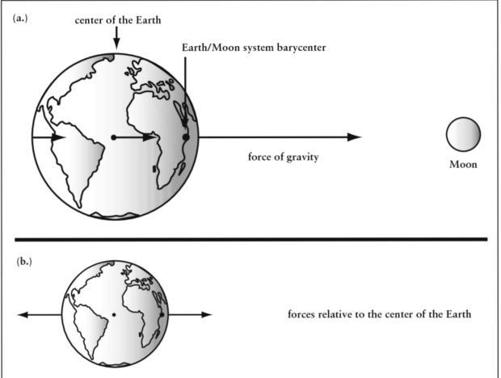
The force of the Moon's gravity on the Earth always "points" toward the Moon. The force gets weaker with distance so that the near side of the Earth is pulled toward the Moon more strongly than the far side. When the force of the Moon's gravity is calculated relative to the Earth/Moon center of mass, the far side of the Earth actually feels a force pointing away from the Moon, while on the near side the force is still toward the Moon. This results in a stretching of the Earth, which is why we have two high tides a day.

But not exactly six hours. If we could hold the Moon stationary for a while, you would indeed feel two high (and two low) tides a day, separated by 12 hours. But as we saw in the last chapter, the Moon rises about an hour later every day, because as the Earth spins, the Moon is also orbiting the Earth. The Moon moves during that day, so we have to spin a little bit extra every day to catch up to it. So instead of there being 24 hours between successive moonrises, there are actually about 25. That means there is a little extra time between high tides; half of that 25 hours, or 12.5 hours. The time of high and low tides changes every day by about a half hour.

An aside: Most people think that only water responds to these tidal forces. That's not true; the ground does, too. The solid Earth isn't really all that solid. It can bend and flex (ask anyone who's ever been in an earthquake). The forces from the Moon actually move the Earth, shifting the ground up and down about 30 centimeters (12 inches) every day. You can't feel it because it happens slowly, but it does happen. There are even atmospheric tides. Air flows better than water, resulting in even more movement. So, the next time someone asks you if the Earth moved, say yes, about a third of a meter.

Incidentally, this puts to rest a common misconception about tides. Some people think that tides affect humans directly. The idea I usually hear is that humans are mostly water, and water responds to the tidal force. But we can see that idea is a bit silly. For one thing, air and solid ground respond to tides as well. But more importantly, humans are too small to be affected noticeably by the tides. The Earth has tides because it's big, thousands of kilometers across. This gives the gravity from the Moon room to weaken. Even a person two meters tall (6 feet 6 inches) feels a maximum difference in gravity of only about 0.000004% from head to foot. The tidal force across the Earth is over a million times stronger than that, so needless to say the tidal force across a human is way too small to be measured. Actually, it's completely overwhelmed by the natural compression of the human body in the standing posi tion; you shrink from gravity more than you are stretched by tides. Even large lakes can barely feel tides; the Great Lakes, for example, have a change in height of only four or five centimeters due to tides. Smaller lakes would have an even smaller change.

As complicated as all that sounds, amazingly, we aren't done yet. Tides due to the Moon are only half the issue. Well, actually, they're two-thirds of the issue. The other third comes from the Sun.

The Sun is vastly more massive than the Moon, so its gravity is far stronger. However, the Sun is a lot farther away. The Earth orbits the Sun in the same way the Moon orbits the Earth, so the same idea applies. The Earth feels a gravitational pull toward the Sun and a centrifugal force away from it. If you do the math, you find out that tides due to the Sun are roughly half the strength of the lunar tides. In the tidal game mass is important but distance even more so. The nearby, low-mass Moon produces more tidal force on the Earth than the much more massive but much farther away Sun. Of the total tidal force exerted on the Earth, two-thirds is from the Moon and one-third is from the Sun.

The Earth is in a constant, complicated tug of war between the Sun and the Moon. There are times when the two objects' forces are in a line. As we saw in the last chapter, "Phase the Nation," when the Moon is new it is near the Sun in the sky, and when it's full it's opposite the Sun. In either case the tidal forces from the Moon and the Sun line up (because, remember, high tides occur simultaneously on opposite sides of the Earth, so it doesn't really matter which side of the Earth you are on), and we get extra-high high tides. It also means the low tides line up, so we get extra-low low tides. These are called spring tides.

When the Sun and Moon are 90 degrees apart in the sky, their forces cancel each other out a bit, and we get tides that aren't quite as low or as high (it's like a lower high tide and higher low tide). These are called neap tides.

Even worse, the Moon orbits the Earth in an ellipse, so sometimes it's closer to us than other times, and the forces are that much greater. The Earth orbits the Sun in an ellipse, too, so we get more exaggerated tides during the time of closest approach to the Sun as well (around January 4 each year). If these two events-closest Moon, and closest point to the Sun-happen at the same time, we get the biggest possible tides. It's not really as big an effect as all that, though; it's only a few percent more. But as you can see, tides are complicated, and the force is never constant.

But there's no reason to stop here. There is another effect. It's subtle, but the implications are quite profound.

As I mentioned, the Earth is spinning on its own axis while the Moon orbits us. The water responds quickly to the tidal force, and "piles up" under the Moon and on the side of the Earth opposite the Moon. However, the Earth is spinning, and its spin is faster (one spin a day) than the Moon's motion around the Earth (one orbit a month). The water wants to pile up under the Moon, but friction with the spinning Earth actually sweeps it forward a bit, ahead of the Moon. The tidal bulge, as it is called, does not point directly to the Moon, but a little in front of it.

So picture this: the bulge nearest the Moon is actually a bit ahead of the Earth-Moon line. That bulge has mass-not a lot, but some. Since it has mass, it has gravity, and that pulls on the Moon. It pulls the Moon forward a bit in its orbit. It acts like a small rocket, pushing the Moon ahead a little. When you push an orbiting object forward, it goes into a higher orbit, that is, one with a larger radius. So, as the tidal bulge on the Earth pulls the Moon forward, the Moon gets farther away from the Earth. This effect has been measured quite accurately. The Moon is actually farther away now than it was a year ago by about 4 centimeters (1.5 inches). Next year it'll be another 4 centimeters farther away, and so on.

Of course, the Moon is pulling on that tidal bulge as well. If the bulge is ahead of the Moon, then the Moon is behind the bulge (relative to the rotation of the Earth). That means it's pulling the bulge backwards, slowing it down. Because of friction with the rest of the Earth, this slowing of the bulge is actually slowing the rotation of the Earth! This is making the day get longer. Again, the effect is small but measurable.

Besides the phase, the most obvious feature of the Moon is that it always shows the same face to us (described in chapter 3, "Idiom's Delight"). This is because the Moon spins once on its axis in the same amount of time it takes to orbit the Earth once. This timing may seem like a miraculous coincidence, but it isn't. Tides force this situation.

All the time the Moon's gravity is exerting a tide on the Earth, the Earth is doing the same thing to the Moon. But the tides on the Moon are 80 times the force of the ones on the Earth, because the Earth is 80 times more massive than the Moon. All of the tidal effects on the Earth are also happening on the Moon, but even faster and stronger.

The Earth raises a big tide on the Moon, stretching it out. There are two high tide bulges on the Moon, right in its solid rock. When the Moon formed, it was closer to the Earth and rotated much faster. The tidal bulge raised by the Earth on the Moon started to slow the Moon's rotation, just as the Earth's high-tide bulge does here. As the Moon slipped farther from the Earth, its rotation slowed, until the rotation period was the same as its revolution period (in other words, its day equaled a month). When that happened, its bulges lined up with the Earth, and the rotation of the Moon became constant; it stopped slowing.

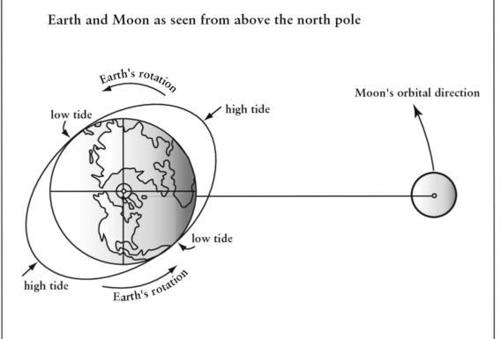
The Earth spins faster (once a day) than the Moon moves around the planet (once a month). A bulge caused by the lunar tide is swept ahead of the Moon by the Earth's rotation. This in turn tugs on the Moon, pulling it faster in its orbit, and moving it away from the Earth by about 4 centimeters per year. It is also slowing the Earth's spin at the same time.

That's why the Moon always shows one face. It's rotating, but the tidal force, well, forced this to happen. It's not coincidence, it's science!

Remember, too, the Earth's rotation is slowing down. Just as the Moon did eons ago, eventually the Earth's rotation will slow down so much that the tidal bulge on the Earth will line up exactly between the centers of the Earth and the Moon. When this happens, the Moon will no longer be pulling the bulge back, and the Earth's spin will stop slowing. The Earth's day will be a month long (and by then the Moon's recession will mean that the month will be longer too, about 40 days). In this time, far in the future, if you were to stand on the Moon and look at the Earth, you would always see the same face of the Earth, just as we see one face of the Moon from the Earth.

This kind of change due to tides is called tidal evolution, and it has affected the Earth and the Moon profoundly. When they were young, the Earth and the Moon were closer together and they both spun much more quickly. But over the billions of intervening years, things have changed drastically.

Once the Earth is rotationally locked with the Moon, there will be no more evolution of the Earth/Moon system from mutual tides. However, there will still be tides from the Sun. They would affect the system, too, but by the time all this happens, the Sun will be well on its way to turning into a red giant, frying the Earth and the Moon. We'll have bigger problems than tides on our hands at that point.

Of course, we aren't the only planet with a moon. Jupiter, for example, has dozens. The tides that Jupiter raises on its moons are hellish; the planet is over 300 times the mass of the Earth. Little To, a moon of Jupiter, orbits its planet at the same distance the Moon orbits the Earth, so it feels tides 300 times stronger than does our Moon. lo is also tidally locked to Jupiter, so it spins once an orbit. If you could stand on Jupiter, you'd always see the same face of To.

But Jupiter has lots of moons, and some of them are big. Ganymede, for example, is bigger than the planet Mercury! These moons all affect each other tidally, too. When one moon passes another, the differential gravity squeezes and stretches the moons, flexing them.

Have you ever taken a metal coat hanger and bent it back and forth really quickly? The metal heats up, possibly enough to burn you. The same thing happens when these moons flex. The change in pressure heats their interiors. It heats lo enough to actually melt its interior. Like the Earth, Io's molten insides break out of the surface in huge volcanoes. The first was discovered when the Voyager I probe cruised past the blighted moon in 1979. Many more have been found since then, and it looks like there are always volcanoes erupting on the poor moon.

The tidal friction also warms the other moons. Europa shows evidence of a liquid-water ocean buried under its frozen surface. That water may be heated by tides from passing moons.

If we look even farther out, we see more tides. Sometimes stars orbit each other in binary pairs. If the stars are very close together, tides can stretch them into egg shapes. If they are even closer, the stars can exchange material, passing streams of gas from one to the other. This changes the stars' evolution, affecting the way they age. Sometimes, if one of the stars is a dense, compact star called a white dwarf, the gas from the more normal star can pile up on the surface of the dwarf. When enough gas accumulates, it can suddenly explode in a cosmic version of a nuclear bomb. The explosion can rip the star to pieces, creating a titanic supernova, which can release as much energy in one second as will the Sun in its entire lifetime.

And we can take one more step out, to a truly grand scale. Whole galaxies are affected by tides, too. Galaxies, collections of billions of stars held together by their own gravity, sometimes pass close to each other. The differential gravity of one passing galaxy can not only stretch and distort but actually tear apart another galaxy. Sometimes, as with the binary stars, the more massive galaxy actually takes material-stars, gas, and dust-from the less massive one in an event called galactic cannibalism. This is hardly a rare event. There's evidence our own Galaxy has done this before, and as a matter of fact, we are currently colliding with a tiny galaxy called the Sagittarius Dwarf. It is passing through the Milky Way near the center, and as it does it loses stars to our much larger and more massive galaxy.

So the next time you're at the beach, think for a moment about what you're seeing. The force of tides may take the water in and out from the shoreline, but it also lengthens our day, pushes the Moon farther away, creates volcanoes, eats stars, and viciously tears apart whole galaxies. Of course, the tides also make it easier to find pretty shells on the coastline. Sometimes it's awesome to think about the universe as a whole, but other times it's okay just to wiggle your toes in the wet sand.