The Philosophy of Physics (2016)
3
Symmetries in Physics
She said, “You’re wearing two different coloured socks.” I said, “Yes, but to me they’re the same because I go by thickness.”
Steven Wright
Modern physics is simply inconceivable without symmetry. As the previous chapter hinted at, symmetries are deeply entangled with the physical laws and conservation principles forming the roots of our best theories. In many ways these theories (and the entities and structures they describe) are defined by their symmetries. As we will see in the chapters that follow, symmetry also lies at the roots of many of the philosophical problems faced by physics: the interpretation game is made much more difficult (or more interesting) by the presence of symmetries.
“Symmetry” in days gone by (and present days by your average ‘person on the street’) had more of an aesthetic meaning: to do with being harmonious, balanced, or well-proportioned - this is the original meaning of the Greek word συμμετρια (‘same measure’). This is a rather static sense: a figure, face, or building can be symmetric without our doing anything to it. But in more modern terms, a symmetry involves observing something before and after some action has been performed on it. It is a kind of ‘change without change’: transformations (or operations) that leave something (or everything) about an object the same as before. They point to an ‘insensitivity’ or ‘blindness’ of some (in cases that interest us, physically) relevant properties or relations (including laws of nature) to some transformation/s that might rotate, shuffle, move, twist, push, or otherwise modify a system in some way. In such a case, the transformations that this holds true for are symmetries, and the object (possibly a physical theory) is said to be invariant (or symmetric) under the transformation.
To pick up Steven Wright’s joke about the socks above: clearly switching a blue for a red sock (a possible operation) will not be a symmetry in terms of how they look, but if we don’t care about color, by focussing on thickness, then, assuming they are the same thickness, switching the socks will be a symmetry in terms of thickness: thickness is preserved or is left invariant with respect to the operation of switching them. Going by thickness determines a different equivalence class of ‘the same things’ (defined by their ‘switchability’ without altering some specific property of interest) than if we go by color.
This brings out an important feature of symmetries: they involve ‘ignoring’ some aspects of a situation and focusing on some relevant structure that is preserved during some operation. That is, when we speak of a transformed object’s being indistinguishable from the original, we usually mean that it is indistinguishable in some relevant respects. In many cases that interest us in this book, it is the laws of nature (and the associated states and observables) that are left invariant with respect to some operation, even though some other aspects might be changed. Sometimes, however, we find that the indistinguishability concerns all relevant respects that would seem to make a physical difference. Such scenarios underlie many philosophical debates since there are both arguments for viewing the transformed states as physically distinct (despite their indistinguishability) and for viewing the transformed states as physically one and the same possibility (that is simply being represented in different ways).
3.1 Symmetry, Invariance, and Equivalence
Symmetries involve equivalence of some sort or another; this is their defining characteristic: two distinct things are equivalent with respect to some feature or features. Given that these things are usually seen to be physically distinct, the equivalence means that for the purposes of physics, ‘either will do’ for formulating some problem: they have the same information content. This translates into a claim about distinguishability, as suggested above: given an equivalence, one will not be able to distinguish (internally: without reference to some other features) which of a pair of symmetric scenarios one is faced with. For example, when sitting on a train at rest on a platform with another train sitting alongside also at rest, when there is some relative motion it is often difficult to tell whether it is your train or the neighboring train that is in motion. Externally, by looking at your position relative to the reference frame provided by the fixed buildings around the train, you can then distinguish rest from motion.
The following (rather lengthy) passage from Galileo’s Dialogues on the Two Chief World Systems - certainly among the most famous pieces of writing in the history of physics - rests on a similar phenomenon:
Shut yourself up with some friend in the main cabin below decks on some large ship, and have with you there some flies, butterflies, and other small flying animals. Have a large bowl of water with some fish in it; hang up a bottle that empties drop by drop into a wide vessel beneath it. With the ship standing still, observe carefully how the little animals fly with equal speed to all sides of the cabin. The fish swim indifferently in all directions; the drops fall into the vessel beneath; and, in throwing something to your friend, you need throw it no more strongly in one direction than another, the distances being equal; jumping with your feet together, you pass equal spaces in every direction.
When you have observed all these things carefully (though doubtless when the ship is standing still everything must happen in this way), have the ship proceed with any speed you like, so long as the motion is uniform and not fluctuating this way and that. You will discover not the least change in all the effects named, nor could you tell from any of them whether the ship was moving or standing still. In jumping, you will pass on the floor the same spaces as before, nor will you make larger jumps toward the stern than toward the prow even though the ship is moving quite rapidly, despite the fact that during the time that you are in the air the floor under you will be going in a direction opposite to your jump. In throwing something to your companion, you will need no more force to get it to him whether he is in the direction of the bow or the stern, with yourself situated opposite. The droplets will fall as before into the vessel beneath without dropping toward the stern, although while the drops are in the air the ship runs many spans. The fish in their water will swim toward the front of their bowl with no more effort than toward the back, and will go with equal ease to bait placed anywhere around the edges of the bowl. Finally the butterflies and flies will continue their flights indifferently toward every side, nor will it ever happen that they are concentrated toward the stern, as if tired out from keeping up with the course of the ship, from which they will have been separated during long intervals by keeping themselves in the air. And if smoke is made by burning some incense, it will be seen going up in the form of a little cloud, remaining still and moving no more toward one side than the other. The cause of all these correspondences of effects is the fact that the ship’s motion is common to all the things contained in it, and to the air also. That is why I said you should be below decks; for if this took place above in the open air, which would not follow the course of the ship, more or less noticeable differences would be seen in some of the effects noted.
In refreshingly simple language, this passage destroys the intuitive reasoning for thinking that we live on a stationary Earth: why don’t we feel the wind in our faces, and why aren’t we thrown off the surface?! Surely, the critics said, we should see and feel that it moves? By linking the Earth whizzing through space to a ship cutting unhindered through the water, Galileo is able to show how we would notice none of the effects we might naively expect to see and feel: the two situations would be internally indistinguishable, and so we could not detect which were true without using some kind of external check. Indeed, for the most part, the objects external to the earth with respect to which we might notice the existence of motion, are so far away that our motion is undetectable - if they were much closer (and/or our speed much (much!) faster) we would indeed notice the motion, and the ship-Earth analogy would break down (though with the experimental outcomes Galileo suggests none the wiser for it).
However, the passage also contains a symmetry principle (Galilean relativity) that expresses the idea that uniform motion is undetectable: the laws of motion are insensitive to transformations that involve switching a pair of uniformly moving reference frames. As Galileo puts it, there would be “not the least change” in the behaviors of objects in the ship. That is, the laws of mechanics (and any experiments you might conduct using them) are invariant with respect to changes of reference frame (in this case the ship) that differ by their (uniform) velocities and positions (and times). This is much easier to experience on an aeroplane (once it has reached a cruising altitude) or a train journey. So long as the going is smooth (and you don’t sneak a peek out of the window), there is no way of telling that you are moving by observing the motion of objects in your vicinity. The air crew merrily stroll down the aisles with drinks, with no spillages - unless turbulence hits (which tends to occur precisely when the drinks are being served, but never mind that …), in which case the motion is non-uniform (this plays a significant role in issues of spacetime ontology, as we see in the next chapter). Hence, we have a change without change: an equivalence (of motions of objects below deck) coupled with a known physical difference (the different states of motion of the ship).
Galilean relativity amounts to the claim that the laws of motion are independent of location, time, orientation, or state of uniform motion at constant velocity (as in the ship example). Changing such features does not change the laws of nature (the same experimental results will emerge regardless of the state of uniform motion), and so these are symmetries of nature. The laws cannot be used to detect absolute locations, times, orientations, or states of uniform motion or rest. Any systems described by such laws are invariant with respect to those transformations that generate changes of location, time, orientation, or state of uniform motion (at constant velocity). This family of transformation-types gives us ten parameters describing ways a system can be altered while leaving the laws undisturbed (Nature’s symmetry group in a classical mechanical world): three parameters to describe spatial translations, a single parameter for temporal translation, reorientations about the three axes of space (three more parameters), and velocity ‘boosts’ in each of the three directions of space (another three parameters). These are known as the Galilean transformations, and they satisfy the mathematical properties of being a group (basically a set of elements - in this case the various transformations - that must satisfy certain conditions on the way the elements combine).1
In more technical terms, for some initial state, represented by coordinates (x, t), we can consider transformations of coordinates of a system of the form:
(3.1)
The meaning of this is that we can act on some point (object) by: rotating it (represented by the matrix A, which is formally an element of the rotation group SO(3)); by shifting it forward (evolving it) in time (represented by t + s, which, mathematically, is a simple shift along the real number line 
); by translating the point by b (where b is a vector in space 3); or by changing the velocity by some ‘boost’ vt (where v is a velocity vector in space). This gives us our ten-parameter group, the Galilean group, Gal for short. A theory that is invariant under these transformations is said to be Galilean invariant. What this means is simply that such transformations (singly, or in combination) ‘make no difference’ from the point of view of physical laws: if x(t) is some solution of the equations of a theory (that is, some trajectory of a system such as a particle) then so is the alteration ϕ(x(t)), with ϕ ∊ Gal. You can’t use such transformations to ‘test’ what your absolute (i.e. relative to space and time, rather than other external objects) state of motion is. Note that ϕ(x(t)) and x(t) represent physically distinct solutions: they are different (as physical states: different positions, velocities, etc.) and yet they are also the same in terms of their intrinsic properties. In terms of the possible-world-talk from earlier, we can say that Galilean transformations leave a theory’s space of physically possible worlds the same so that applying one of the transformations to a state (i.e. of a physically possible world) leads to another physically possible world (see §3.2 for more on the connection between laws and possible worlds).
Newton’s laws of motion are independent of location, time, orientation, or state of uniform motion at constant velocity. Hence, they are Galilean invariant: they take the same form in reference frames related by the corresponding transformations. This implies that we can’t detect position and velocity by any process governed by Newton’s laws: a kind of ‘conspiracy of nature’ hides any such transformations from our gaze. As we shall see, this conspiracy lies at the center of a justly famous debate between Newton and Gottfried Leibniz. In situations where the solution concerns the entire material content of the universe, performing a Galilean transformation appears to generate something that doesn’t differ physically: yet if we think of space and time as giant containers in which the transformations are carried out then they must be physically distinct regardless.
At the root of the debate is the fact that for each set of such parameters there is some piece of physical structure that is rendered unobservable. In the case of the translation piece of the Galilean group (the bit that shifts objects in space), one cannot observe absolute locations (i.e. positions relative to space itself). Invariance under time shifts renders absolute time location unobservable (you can’t tell when you are relative to time itself). Invariance under rotations renders absolute orientation unobservable (you can’t tell which way you are pointing relative to space itself). And, finally, invariance under changes in velocity renders absolute velocity (or absolute rest) unobservable (you can’t tell how fast you are moving relative to space itself). That’s a lot of unobservable structure. In general, the more symmetries one has the more unobservable structure one introduces since such symmetries destroy our ability to discern differences between certain physical situations, and so we can’t tell which of some set of possibilities we are in fact observing (assuming there is indeed a fact of the matter).
There is a standard method of removing this unobservable structure (formally at least), if we decide that keeping it is not to our taste, by ‘quotienting’ (or ‘modding’) out the symmetry. What this amounts to, in simple terms, is identifying all of the symmetric possibilities (those directly related by some symmetry operation), forming (and subsequently working with) an ‘equivalence class’ - an equivalence class of possibilities can simply be understood to contain elements any of which would be ‘up to the task’ of representing some physical situation so that there are many possible mathematical descriptions of the same situation. The symmetry transformations can then be seen to take us from one possible description to another possible description. The quotienting procedure then reduces this multiplicity of indistinguishable possibilities to a single possibility: the space of physically possible worlds is thus reduced in size. In a sense, as we see in the next chapter, the battle between Leibniz and Newton centered on just this feature: how big is the space of possibilities? Should we include indistinguishable possibilities or eliminate them?
Finally, just for completeness, we should point out that (in certain special important cases involving continuous symmetries) each of the sets of parameters is associated with a conserved quantity as well as some unobservable structure. Translation symmetry leads to conservation of momentum; time translation symmetry to conservation of energy; and rotation symmetry to conservation of angular momentum. If there weren’t these stable features under the various operations, then one could use the alterations to detect location, time, velocity, and orientation. That we cannot do this also points to features of the spatiotemporal system itself: it must be isotropic (with no preferred direction) and homogeneous (look the same everywhere and everywhen). This is a general feature of symmetries: what kinds of transformation leave the laws unchanged are indicative of the underlying physical structures in or on which the operations are carried out. Naturally, the kinds of objects that are left most unperturbed under various operations (those that are most insensitive to a barrage of transformations that attempt to change them) are going to be homogeneous among themselves - we find this even with quantum particles, which are identical in terms of their intrinsic properties, so that switching them leaves the laws of quantum mechanics none the wiser. Likewise, what is observable according to the theory is equally unimpressed by such switchings - in which case the permutation of particles constitutes what is called an automorphism of the set of observables, mapping it back to itself (if the equivalence mapping is to another object distinct from the first then it is generically known as an ‘isomorphism’). We discuss this curious ‘permutation symmetry’ of quantum objects in §7.5.
3.2 Symmetries, Laws, and Worlds
Jennan Ismael and Bas van Fraassen [27] claim that a physical theory can usefully be split into two main ingredients: ‘theoretical ontology’ and ‘laws of nature.’ The ontology is to be thought of in terms of a metaphysical possibility space (a space embodying what kinds of entities, properties, and relations are allowed by the theory). These possible worlds (being ‘entire world histories’) correspond to state space trajectories. Neither of these spaces is yet physical, in the sense of satisfying the dynamical equations of some theory (the laws, that is). The role of the laws is to then restrict this rather liberal metaphysical possibility space (or the associated mathematical state space) to a smaller family of physically (or, as philosophers of science say, nomologically) possible worlds (those in which the entities, properties, and relations satisfy the laws). Hence, only some of the possible worlds (a subset of the space of possible worlds) is associated with the physically possible trajectories.
This notion of (physical) possibility space is deeply entangled with both the definition of a theory, then, but also with interpretation: the provision of the ontology (the worlds) is equivalent to giving an interpretation (a way the world could be according to the theory). The idea is that a theory presents us with a mathematical space, with a certain geometrical structure appropriate to the system it is invoked to model, where the points of this space represent physically possible states of affairs for a system modeled by the theory. Symmetries can easily be realized in terms of these such spaces. If a theory admits symmetries then: (1) distinct points of the space will be related by symmetries; (2) these points will form an equivalence class (an orbit in the jargon); and (3) elements of this equivalence class will represent qualitatively identical possibilities: the symmetries simply map a set of individuals (in a domain) onto other individuals in such a way as to preserve the relevant relations and properties (this is the meaning of the term ‘automorphism’ from earlier).
This framework lets us now distinguish between two types of symmetry, which is important from the point of view of possible worlds (i.e. distinct physical possibilities): symmetry proper and gauge symmetry. According to the former, the distinct points related by the symmetry transformation are taken to represent physically distinct possibilities - that is, the representation relation is one-to-one between elements of the space (trajectories) and physically possible worlds. But in the case of gauge symmetries this direct link breaks down so that many trajectories correspond to one and the same physically possible world - the representation relation is therefore many-to-one (we discuss this curious symmetry further in §8.3). The idea is that we would have some equations of motion defining some theory, which will admit some symmetric solutions. This has important interpretative consequences since the latter gauge symmetries open up the possibility of treating the equivalence class itself as the object that we should be committed to (as mentioned earlier). This is how symmetries begin to complicate the interpretation game.
3.3 Some Important Distinctions
The study of symmetries in physics (and elsewhere) is buried in jargon. This is no bad thing: in this case it means that they are well understood, and so involve lots of fine distinctions in classifying them. In this section we briefly introduce some of the most important distinctions that will be invoked in the remainder of the book.
Geometric and Dynamical
A very special class of symmetries relates to the properties of space, time, and spacetime. These are known as ‘geometric (or universal) symmetries’ and they are the basis of the laws of many theories. Indeed, one can work backwards (from certain laws to certain features of the space and time) or forwards (from features of space and time to the laws). What is special about geometric laws is that since every system exists within spacetime every system is thereby subject to symmetries pertaining to spacetime: hence, they are universal.
There are other symmetries that apply to some particularities of the system that is invariant under them. For example, there is a symmetry according to which the laws of quantum mechanics are invariant under changes of absolute phase of particles (where the phase comes from the strange wavelike aspects of particles in quantum mechanics). Quite naturally, this is grounded in the nature of the particles and in the existence of their phases, which is a feature not universally shared by all things. These are known as dynamical symmetries since they refer to specific physical theories (or rather the forces or interactions these theories describe - usually post-classical ones).
Eugene Wigner (who named this distinction: see his book mentioned in the Further Readings at the end of this chapter) grounds it in a distinction based on events: the geometric symmetries don’t change the events (by which he clearly means observable, qualitative stuff: ‘phenomena’), but just their spatiotemporal locations, orientations, and motions. Moreover, the formulation of the invariances makes reference only to events and their correlations, independently of the laws or the specific constitution of the physical systems: all that matters is the independence of the events from locations (regardless of what the events are made up of) and so on. The dynamical symmetries on the other hand involve the laws of physics directly in their formulation, explicitly referring to the specifics of the objects and interactions.
This distinction can usually be mapped onto a further distinction between ‘internal’ and ‘external’ symmetries, where the former refers to the fact that the transformations are not spatiotemporal but instead refer to some ‘abstract’ internal space. Many properties of quantum particles show this independence from spacetime. Such symmetries are further from experience, of course, because experience demands at least some semblance of a spatiotemporal framework to be experienced. As such internal symmetries are inferred from data about the forces, where the process of inference is more elaborate than for geometric symmetries.
Continuous and Discrete
The spacetime symmetries are said to be continuous symmetries since each transformation can be built (or reached) by repeatedly applying an infinitesimal transformation. Hence, a rotation from some original position to a 40-degree turn does not involve a jump, but must involve an infinite sequence of intermediate tiny rotations. Such symmetries, involving the addition of infinitesimal in-between stages, are sometimes known as ‘proper’ symmetries, since they involve physically realistic transformations that we could imagine doing with real objects in real space. By contrast we have discrete symmetries that do not involve intermediate steps through the points of space connecting one state (the original) with another (the end point of the transformation). An example is reflection about some axis, which no continuous sequence of rigid (infinitesimal) motions can bring about. A reflection can turn a left hand into a right hand (look at your hand in a mirror!). This means that reflection symmetry involves a left-right symmetry - a mirror doesn’t actually transform your right hand into a left hand of course, it just shows what it would look like if you somehow managed it. Time reflection is another example: what it means is that if a process in one temporal direction is ‘allowed’ (i.e. a solution of some equations of motion), then so is its time-reverse (where the ‘movie’ of the process is played backwards).
These are, unsurprisingly, known as ‘improper’ since it is hard to envisage such jumps occurring in physical spacetime. In other words, we can’t transform a left hand to a right hand by performing smooth, rigid, continuous motions. (Clearly the ‘rigidity’ is required here since otherwise we could just ‘squish’ a left hand like plasticine to such a degree that it looks like a right hand.)
As with the symmetries appearing in the Galilean group, such symmetries are nonetheless expected to be obeyed by the laws and quantities of physics given assumptions about the isotropy and homogeneity of space and time. However, we will see that philosophical novelties appear in the case of discrete symmetry groups.
Local and Global
As the name suggests, a global symmetry is one that involves transformations that act in the same way at every point of space, so that in, e.g. the case of a translation performing it globally would mean shifting everything in the same way. This might be taken to mean that they only ever apply to everything (i.e. the universe), but that’s a mistake: Galileo’s ship argument involves a global symmetry, namely a uniform velocity boost. Problems emerge, as we see in the next chapter, when we apply such global symmetry transformations to the universe as a whole. It appears that while Galileo’s transformed ships will clearly be physically distinct scenarios (e.g. only one’s moving away from the shore while the other is anchored), in the case of shifted universes as a whole, it’s hard to see that there is any difference at all: there is no comparable sea shore from which to judge the differences.
A local symmetry, by contrast, involves transformations that can be applied at spacetime points independently of the other points. If the space-time has infinitely many points then this implies that the symmetry group is infinite-dimensional (has infinitely many parameters, compared to the ten of the Galilean group), since it can act differently at each one of those points. These local symmetries are associated with internal symmetries since they cannot be couched in terms of conserved quantities observable through the various correlations of events (as with the time-interval between events being observable rather than the absolute temporal location, pointing to time-translation invariance). General relativity has such a local spacetime symmetry based on Diff(ℳ), the group of diffeomorphisms of a manifold (spacetime, that is) - these diffeomorphisms essentially just turn one manifold into another by moving the points of the spacetime manifold around. What this means, very roughly, is that the laws of general relativity (Einstein’s field equations for the gravitational field) are invariant with respect to any smooth transformation of the points of spacetime that keeps the structure of the spacetime manifold intact (which means, again very roughly, that the transformation does not end up ‘tearing’ the spacetime manifold or putting holes in it). To connect up to the discussion about laws, symmetries, and possible worlds: if we have some solution of the Einstein equations (which represents a possible world), then if we transform it by applying one of these diffeomorphisms we have ourselves another possible world that satisfies the laws of general relativity. In this sense, the group of diffeomorphisms is the symmetry group of the theory.2
Local symmetry is rather more surprising: clearly if we shift everything in the same way by the same amount (moving everything we can see, including ourselves, by the same amount) then we won’t be surprised to see that things look the same. But if we shifted everything in different ways at all the different points (so that the transformation is dependent on the particular spacetime point), then we’d surely be very surprised if things (observables and laws) stayed the same! Local symmetries have just this property. Since they lead to no observable changes, they are usually considered to be a feature of the mathematical representation used to model reality, rather than part of reality itself, as with the symmetries used in Galileo’s ship - though there is controversy over this point, some of which we return to. Such symmetries are also called gauge symmetries - a topic we return to in §8.3.
Passive and Active
Transformations (otherwise known as ‘mappings’ or just ‘maps’) in the sense used in this book simply refer to an association of one object (e.g. a point in spacetime) to another (e.g. another point in spacetime) - the new point that results from the transformation is the image under the mapping. Importantly, whatever is sitting at such a point is ‘carried along’ as if on a wave to the image. Because of this joint effect, we will generally be loose when talking about what gets mapped around. Symmetries are quite clearly mappings in this sense and can transform solutions of a theory’s equations into other solutions (e.g. carrying a ship in one region of space to another region of space).
We can consider these transformations in either a ‘passive’ or an ‘active’ sense. The former means that it is the reference frame of the observer that is transformed - for example, I might stand on my head to see if some property (or all properties) of an object are left ‘looking the same.’ The latter means that I save my poor head and turn the object on its head instead, still checking to see if the properties are left unchanged or not. When we are dealing with a symmetry then the active and passive interpretations are equivalent: what the active transformation does is exactly compensated for by an equal and opposite (i.e. inversely related) passive transformation: doing an active followed by a passive transformation cancels out so that nothing ends up being done.
The simplest way to see that this is so involves looking at a transformation through a coordinate system. Let’s consider simply rotating a ball, with starting coordinates (Fx, Fy), by θ (some number of degrees of rotation) relative to an origin. On the active interpretation, this would involve a literal moving of the ball, from F to F′ (by an amount θ) in fig. 3.1, all taking place in a fixed background coordinate system (x, y).
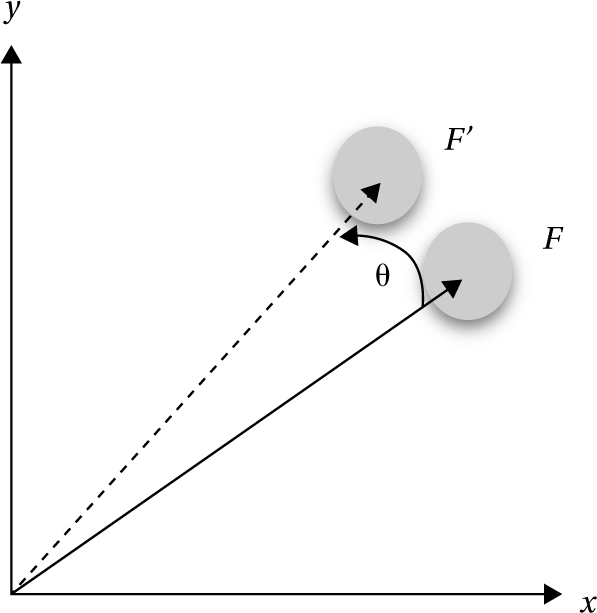
Fig. 3.1 Active transformation of the ball, about the origin, keeping the coordinate system fixed.
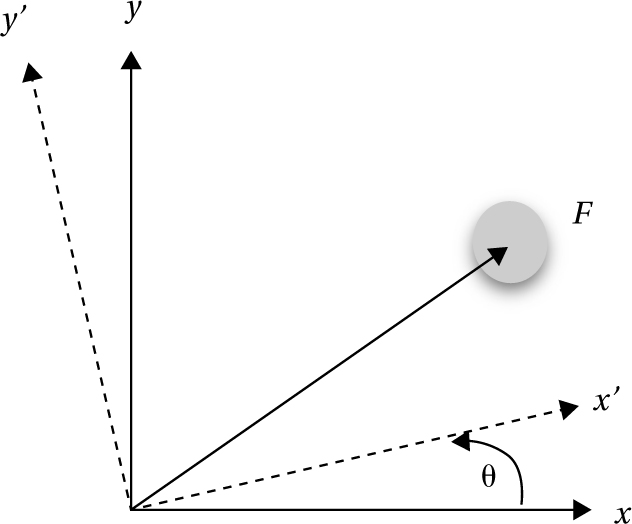
Fig. 3.2 Passive transformation of the ball, keeping the ball fixed but now shifting the coordinate system.
On a passive approach, the ball stays firmly where it is, but now we move our axes by the same amount θ, seen in fig. 3.2.
Being inverses of one another, combining the two transformations leaves us where we started (fig. 3.3).
Hence, it is a simple case of shifting the measured system versus shifting the coordinate system (the system of measurement). The next chapter puts the results from this and the earlier chapter to work in specific examples.
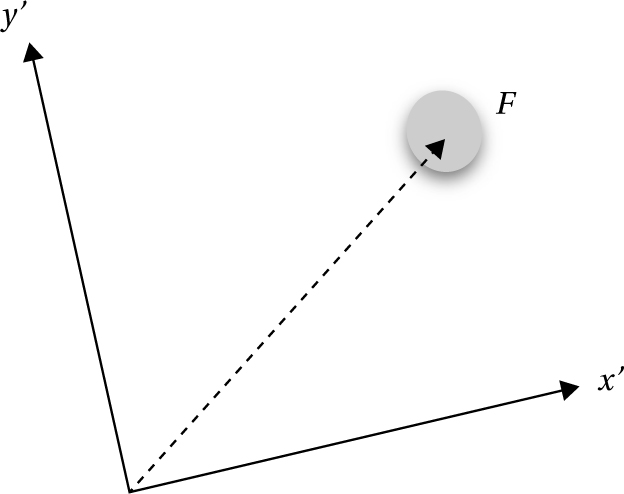
Fig. 3.3 Combining the active and passive transformations in the case of a symmetry leaves the original situation ‘untouched.’
3.4 Further Readings
The philosophical discussion of symmetries naturally involves the usage of mathematics. The readings below give excellent guides to both the technical and conceptual elements.
Fun
· Hermann Weyl (1952) Symmetry. Princeton University Press.
- Classic discussion of symmetry, which covers examples of symmetry in art, nature, and science and introduces with brilliant clarity the technical notions involved.
· Kristopher Tapp (2010) Symmetry: A Mathematical Exploration. Springer.
- Though the title states that this is a “Mathematical Exploration,” it is exceptionally easy to read, and will lead the reader to a good intuitive grasp of the relationship between group theory and symmetry.
Serious
· Elena Castellani and Katherine Brading, eds. (2003) Symmetry in Physics: Philosophical Reflections. Cambridge University Press.
- Superb collection of readings, old and new, on philosophical aspects of symmetry.
Connoisseurs
· Eugene Wigner (1967) Symmetries and Reflections. Indiana University Press.
- Much of our terminology and concepts come from this book. Written in crystal clear prose.
Notes
1 Any book on group theory will explain this basic idea - a good choice for those interested in physics applications is Chris Isham’s Lectures on Groups and Vector Spaces for Physicists (World Scientific, 1989). The Galilean group is strictly speaking a ‘Lie group’ since the various parameters are continuous. A finite rotation, of a planet for example, would be generated (or ‘built up’) by the accumulation of lots of infinitesimal rotations. A useful book on Lie groups, for those already acquainted with vectors and matrices, is Harriet Pollatsek’s, Lie Groups: A Problem-Oriented Introduction via Matrix Groups (Mathematical Association of America, 2009).2 This is very over-simplified and there are many more subtle issues surrounding the proper interpretation of the symmetry group of general relativity, but these are too technical to go into here. The interested reader should consult §4 of C. Rovelli and M. Gaul, “Loop Quantum Gravity and the Meaning of Diffeomorphism Invariance” (in J. Kowalski-Glikman (ed.) Towards Quantum Gravity, Springer: pp. 277-324).