Why Does E=mc²? (And Why Should We Care?) - Brian Cox, Jeffrey R. Forshaw (2009)
Chapter 2. The Speed of Light
Michael Faraday, the son of a Yorkshire blacksmith, was born in south London in 1791. He was self-educated, leaving school at fourteen to become an apprentice bookbinder. He engineered his own lucky break into the world of professional science after attending a lecture in London by the Cornish scientist Sir Humphry Davy in 1811. Faraday sent the notes he had taken at the lecture to Davy, who was so impressed by Faraday’s diligent transcription that he appointed him his scientific assistant. Faraday went on to become a giant of nineteenth-century science, widely acknowledged to have been one of the greatest experimental physicists of all time. Davy is quoted as saying that Faraday was his greatest scientific discovery.
As twenty-first-century scientists, it is easy to look back at the early nineteenth century with envious eyes. Faraday didn’t need to collaborate with 10,000 other scientists and engineers at CERN or launch a double-decker-bus-sized space telescope into high-earth orbit to make profound discoveries. Faraday’s “CERN” fitted comfortably onto his bench, and yet he was able to make observations that led directly to the destruction of the notion of absolute time. The scale of science has certainly changed over the centuries, in part because those areas of nature that do not require technologically advanced apparatus to observe them have already been studied in exquisite detail. That’s not to say there aren’t examples in science today where simple experiments produce important results, just that to push back the frontiers across the board generally requires complicated machines. In early Victorian London, Faraday needed nothing more exotic or expensive than coils of wire, magnets, and a compass to provide the first experimental evidence that time is not what it seems. He gathered this evidence by doing what scientists like to do best. He set up all the paraphernalia associated with the newly discovered electricity, played around, and watched carefully. You can almost smell the darkly varnished bench mottled with shadows of coiled wire shifting in the gaslight, because even though Davy himself had dazzled audiences with demonstrations of electric lights in 1802 at the Royal Institution, the world had to wait until much later in the century for Thomas Edison to perfect a useable electric lightbulb. In the early 1800s, electricity was physics and engineering at the frontier of knowledge.
Faraday discovered that if you push a magnet through a coil of wire, an electric current flows in the wire while the magnet is moving. He also observed that if you send a pulse of electric current along a wire, a nearby compass needle is deflected in time with the pulse. A compass is nothing more than a magnet detector; when no electricity is pulsing through the wire, it will line up with the direction of the earth’s magnetic field and point toward the North Pole. The pulse of electricity must therefore be creating a magnetic field like the earth’s, although more powerful since the compass needle is wrenched away from magnetic north for a brief instant as the pulse moves by. Faraday realized that he was observing some kind of deep connection between magnetism and electricity, two phenomena that at first sight seem to be completely unrelated. What does the electric current that flows through a lightbulb when you flick a switch on your living room wall have to do with the force that sticks little magnetic letters to your fridge door? The connection is certainly not obvious, and yet Faraday had found by careful observation of nature that electric currents make magnetic fields, and moving magnets generate electric currents. These two simple phenomena, which now go by the name of electromagnetic induction, are the basis for generating electricity in all of the world’s power stations and all of the electric motors we use every day, from the pump in your fridge to the “eject” mechanism in your DVD player. Faraday’s contribution to the growth of the industrial world is incalculable.
Advances in fundamental physics rarely come from experiments alone, however. Faraday wanted to understand the underlying mechanism behind his observations. How could it be, he asked, that a magnet not physically connected to a wire can nevertheless cause an electric current to flow? And how can a pulse of electric current wrench a compass needle away from magnetic north? Some kind of influence must pass through the empty space between magnet, wire, and compass; the coil of wire must feel the magnet passing through it, and the compass needle must feel the current. This influence is now known as the electromagnetic field. We’ve already used the word “field” in the context of the earth’s magnetic field, because the word is in everyday usage and you probably didn’t notice it. In fact, fields are one of the more abstract concepts in physics. They are also one of the most necessary and fruitful for developing a deeper understanding. The equations that best describe the behavior of the billions of subatomic particles that make up the book you are now reading, the hand with which you are holding the book in front of your eyes, and indeed your eyes, are field equations. Faraday visualized his fields as a series of lines, which he called flux lines, emanating from magnets and current-carrying wires. If you have ever placed a magnet beneath a piece of paper sprinkled with iron filings, then you will have seen these lines for yourself. A simple example of an everyday quantity that can be represented by a field is the air temperature in your room. Near the radiator, the air will be hotter. Near the window, it will be cooler. You could imagine measuring the temperature at every point in the room and writing down this vast array of numbers in a table. The table is then a representation of the temperature field in your room. In the case of the magnetic field, you could imagine noting the deflection of a little compass needle at every point, and in that way you could form a representation of the magnetic field in the room. A subatomic-particle field is even more abstract. Its value at a point in space tells you the chance that the particle will be found at that point if you look for it. We will encounter these fields again in Chapter 7.
Why, you might legitimately ask, should we bother to introduce this rather abstract notion of a field? Why not stick to the things we can measure: the electric current and the compass needle deflections? Faraday found the idea attractive because he was at heart a practical man, a trait he shared with many of the great experimental scientists and engineers of the Industrial Revolution. His instinct was to create a mechanical picture of the connection between moving magnets and coils of wire, and for him the fields bridged the space between them to forge the physical connection his experiments told him must be present. There is, however, a deeper reason why the fields are necessary, and indeed why modern physicists see the fields as being every bit as real as the electric current and compass deflections. The key to this deeper understanding of nature lies within the work of Scottish physicist James Clerk Maxwell. In 1931, on the centenary of Maxwell’s birth, Einstein described Maxwell’s work on the theory of electromagnetism as “the most profound and the most fruitful that physics has experienced since the time of Newton.” In 1864, three years before Faraday’s death, Maxwell succeeded in writing down a set of equations that described all of the electric and magnetic phenomena Faraday and many others had meticulously observed and documented during the first half of the eighteenth century.
Equations are the most powerful of tools available to physicists in their quest to understand nature. They also are often among the scariest things most people meet during their school years, and we feel it necessary to say a few words to the apprehensive reader before we continue. Of course, we know that not everyone will feel that way about mathematics, and we ask for a degree of patience from more confident readers and hope they won’t feel too patronized. At the simplest level, an equation allows you to predict the results of an experiment without actually having to conduct it. A very simple example, which we will use later in the book to prove all sorts of incredible results about the nature of time and space, is Pythagoras’ famous theorem relating the lengths of the sides of a right-angled triangle. Pythagoras states that “the square of the hypotenuse is equal to the sum of the squares of the other two sides.” In mathematical symbols, we can write Pythagoras’ theorem as x2 + y2 = z2, where z is the length of the hypotenuse, which is the longest side of the right-angled triangle, and x and y are the lengths of the other two sides. Figure 1 illustrates what is going on. The symbols x, y, and z are understood to be placeholders for the actual lengths of the sides and x2 is mathematical notation for x multiplied by x. For example, 32 = 9, 72 = 49 and so on. There is nothing special about using x, y, and z; we could use any symbol we like as a placeholder. Perhaps Pythagoras’ theorem looks more friendly if we write it as![]() = ☺2. This time the smiley-face symbol represents the length of the hypotenuse. Here is an example using the theorem: If the two shorter sides of the triangle are 3 centimeters (cm) and 4 centimeters long, then the theorem tells us that the length of the hypotenuse is equal to 5 centimeters, since 32 + 42 = 52. Of course, the numbers don’t have to be whole numbers. Measuring the lengths of the sides of a triangle with a ruler is an experiment, albeit a rather dull one. Pythagoras saved us the trouble by writing down his equation, which allows us to simply calculate the length of the third side of a triangle given the other two. The key thing to appreciate is that for a physicist, equations express relationships between “things” and they are a way to make precise statements about the real world.
= ☺2. This time the smiley-face symbol represents the length of the hypotenuse. Here is an example using the theorem: If the two shorter sides of the triangle are 3 centimeters (cm) and 4 centimeters long, then the theorem tells us that the length of the hypotenuse is equal to 5 centimeters, since 32 + 42 = 52. Of course, the numbers don’t have to be whole numbers. Measuring the lengths of the sides of a triangle with a ruler is an experiment, albeit a rather dull one. Pythagoras saved us the trouble by writing down his equation, which allows us to simply calculate the length of the third side of a triangle given the other two. The key thing to appreciate is that for a physicist, equations express relationships between “things” and they are a way to make precise statements about the real world.
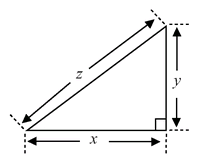
FIGURE 1
Maxwell’s equations are mathematically rather more complicated, but in essence they do exactly the same kind of job. They can, for example, tell you in which direction a compass needle will be deflected if you send a pulse of electric current through a wire without having to look at the compass. The wonderful thing about equations, however, is that they can also reveal deep connections between quantities that are not immediately apparent from the results of experiments, and in doing so can lead to a much deeper and more profound understanding of nature. This turns out to be emphatically true of Maxwell’s equations. Central to Maxwell’s mathematical description of electrical and magnetic phenomena are the abstract electric and magnetic fields Faraday first pictured. Maxwell wrote down his equations in the language of fields because he had no choice. It was the only way of bringing together the vast range of electric and magnetic phenomena observed by Faraday and his colleagues into a single unified set of equations. Just as Pythagoras’ equation expresses a relationship between the lengths of the sides of a triangle, Maxwell’s equations express relationships between electric charges and currents and the electric and magnetic fields they create. Maxwell’s genius was to invite the fields to emerge from the shadows and take center stage. If, for example, you asked Maxwell why a battery causes a current to flow in a wire, he might say, “because the battery causes there to be an electric field in the wire, and the field makes the current flow.” Or if you asked him why a compass needle deflects near a magnet, he might say, “because there is a magnetic field around the magnet, and this causes the compass needle to move.” If you asked him why a moving magnet causes a current to flow inside a coiled wire, he might answer that there is a changing magnetic field inside the coiled wire that causes an electric field to appear in the wire, and this electric field causes a current to flow. In each of these very different phenomena, the description always comes back to the presence of electric and magnetic fields, and the interaction of the fields with each other. Achieving a simpler and more satisfying view of many diverse and at first sight unrelated phenomena through the introduction of a new unifying concept is a common occurrence in physics. Indeed, it could be seen as the reason for the success of science as a whole. In Maxwell’s case, it led to a simple and unified picture of all observed electric and magnetic phenomena that worked beautifully in the sense that it allowed for the outcome of any and all of the pioneering benchtop experiments of Faraday and his colleagues to be predicted and understood. This was a remarkable achievement in itself, but something even more remarkable happened during the process of deriving the correct equations. Maxwell was forced to add an extra piece into his equations that was not mandated by the experiments. From Maxwell’s point of view, it was necessary purely to make his equations mathematically consistent. Contained in this last sentence is one of the deepest and in some ways most mysterious insights into the workings of modern science. Physical objects out there in the real world behave in predictable ways, using little more than the same basic laws of mathematics that Pythagoras probably knew about when he set about to calculate the properties of triangles. This is an empirical fact and can in no sense be said to be obvious. In 1960, the Nobel Prize-winning theoretical physicist Eugene Wigner wrote a famous essay titled “The Unreasonable Effectiveness of Mathematics in the Natural Sciences,” in which he stated that “it is not at all natural that laws of Nature exist, much less that man is able to discover them.” Our experience teaches us that there are indeed laws of nature, regularities in the way things behave, and that these laws are best expressed using the language of mathematics. This raises the interesting possibility that mathematical consistency might be used to guide us, along with experimental observation, to the laws that describe physical reality, and this has proved to be the case time and again throughout the history of science. We will see this happen during the course of this book, and it is truly one of the wonderful mysteries of our universe that it should be so.
To return to our story, in his quest for mathematical consistency, Maxwell added the extra piece, known as the displacement current, to the equation describing Faraday’s experimental observations of the deflection of compass needles produced by electric currents flowing in wires. The displacement current was not necessary to describe Faraday’s observations, and the equations described the experimental data of the time with or without it. Initially unbeknownst to Maxwell, however, with this simple addition his beautiful equations did far more than describe the workings of electric motors. With the displacement current included, a deep relationship between the electric and magnetic fields emerges. Specifically, the new equations can be recast into a form known as wave equations, which not surprisingly describe the motion of waves. Equations that describe the propagation of sound through the air are wave equations, as are equations that describe the journey of ocean waves to the shore. Quite unexpectedly, Maxwell’s mathematical description of Faraday’s experiments with wires and magnets predicted the existence of some kind of traveling waves. But whereas ocean waves are disturbances traveling through water, and sound waves are made up of moving air molecules, Maxwell’s waves comprise oscillating electric and magnetic fields.
What are these mysterious oscillating fields? Imagine an electric field beginning to grow because Faraday generates a pulse of electric current in a wire. We have already learned that as the pulse of electric current passes along the wire, a magnetic field is generated (remember that Faraday observed that a compass needle in the vicinity of the wire is deflected). In Maxwell’s language, the changing electric field generates a changing magnetic field. Faraday also tells us that when we change a magnetic field by pushing a magnet through a coil of wire, an electric field is generated, which causes a current to flow in the wire. Maxwell would say that a changing magnetic field generates a changing electric field. Now imagine removing the currents and the magnets. We are left with just the fields themselves, swinging backward and forward as changes in one generate changes in the other. Maxwell’s wave equations describe how these two fields are linked together, oscillating backward and forward. They also predict that these waves must move forward with a particular speed. Perhaps not surprisingly, this speed is fixed by the quantities Faraday measured. In the case of sound waves, the wave speed is approximately 330 meters per second, just a little bit faster than a passenger airplane. The speed of sound is fixed by the details of the interactions between the air molecules that carry the wave. It changes with varying atmospheric pressure and temperature, which in turn describe how closely the air molecules get to each other and how fast they bounce off each other. In the case of Maxwell’s waves, the speed is predicted to be equal to the ratio of the strengths of the electric and magnetic fields, and this ratio can be measured very easily. The strength of the magnetic field can be determined by measuring the force between two magnets. The word “force” will crop up from time to time, and by it we mean the amount by which something is pushed or pulled. The amount of push/pull can be quantified and measured, and if we are trying to understand how the world works, it should come as little surprise that we will want to understand how forces originate. In an equally simple way, the electric field strength can be measured by charging up two objects and measuring the force between them. You may have inadvertently experienced that “charging up” process yourself. Perhaps you’ve walked around over a nylon carpet on a dry day and then received an electric shock when you tried to open a door with a metal handle. This unpleasant door-opening experience occurs because you have rubbed electrons, the fundamental particles of electricity, off the carpet and into the soles of your shoes. You have become electrically charged, and this means that an electric field exists between you and the door handle. Given the chance when you grab hold of the door handle, this field will cause an electric current to flow, just as Faraday found in his experiments.
By carrying out such simple experiments, scientists can measure the strengths of the electric and magnetic fields, and Maxwell’s equations predict that the ratio of strengths gives the speed of the waves. What, then, is the answer? What did Faraday’s benchtop measurements, coupled with Maxwell’s mathematical genius, predict for the speed of the electromagnetic waves? This is one of many key moments in our story. It is a wonderful example of why physics is a beautiful, powerful, and profound subject: Maxwell’s waves travel at 299,792,458 meters per second. Astonishingly, this is the speed of light—Maxwell had stumbled across an explanation of light itself. You see the world around you because Maxwell’s electromagnetic field drives itself through the darkness and into your eyes, at a speed predictable using only a coil of wire and a magnet. Maxwell’s equations are the crack in the door through which light enters our story in a way that is every bit as important as the discoveries of Einstein that they triggered. The existence in nature of this special speed, a single, unchanging, 299,792,458 meters per second, will lead us in the next chapter, just as it led Einstein, to jettison the notion of absolute time.
The attentive reader might notice a puzzle here, or at least some sloppy writing on our part. Given what we said in Chapter 1, it clearly makes no sense to quote a speed without specifying relative to what that speed is defined, and Maxwell’s equations make no mention of this problem. The speed of the waves—that is, the speed of light—appears as a constant of nature, the relationship between the relative strengths of the electric and magnetic fields. Nowhere in this elegant mathematical structure is there a place for the speed of the source of the waves, or indeed the receiver. Maxwell and his contemporaries knew this, of course, but it didn’t worry them unduly. This is because most, if not all, of the scientists of the time believed that all waves, including light, must travel in some kind of medium; there must be some “real stuff ” that is doing the waving. They were practical folk in Faraday’s mold, and to them things don’t just wave on their own with no support. Water waves can exist only in the presence of water, and sound waves travel only in the presence of air or some other substance, but certainly not in a vacuum: “In space, no one can hear you scream.”
So the prevailing view at the end of the nineteenth century was that light must travel through a medium, and this medium was known as the ether. The speed that appeared in Maxwell’s equations then had a very natural interpretation as the speed of light relative to the ether. This is exactly analogous to the propagation of sound waves through air. If the air is at a fixed temperature and pressure, then sound will always travel at a constant speed, which depends only on the details of the interactions between the air molecules, and has nothing to do with the motion of the source of the waves.
The ether must be a strange kind of stuff, though. It must permeate all of space, since light travels across the voids between the sun and earth and the distant stars and galaxies. When you walk down the street, you must be moving through the ether, and the earth must be passing through the ether on its yearly journey around the sun. Everything that moves in the universe must make its way through the ether, which must offer little or no resistance to the motion of solid objects, including things as large as planets. For if the ether did offer resistance to the motion of solid objects, the earth would have been slowed down during each of its 5 billion solar orbits, just as a ball bearing slows down when dropped into a jar of molasses, and our Earth years would gradually change in length. The only reasonable assumption must be that the earth and all objects move through the ether unimpeded. You may think that this would make its discovery impossible, but the Victorian experimentalists were nothing if not ingenious, and in a series of wonderfully high-precision experiments beginning in 1881, Albert Michelson and Edward Morley set out to detect the apparently undetectable. The experiments were beautifully simple in conception. In Bertrand Russell’s excellent book on relativity written in 1925, he likens the earth’s motion through the ether to going for a circular walk on a windy day; at some point you will be walking against the wind, and at some point with it. In a similar fashion, since the earth is moving through the ether as it orbits the sun, and the earth and sun together are flying through the ether in their journey around the Milky Way, then at some point in the year the earth must be moving against the ether wind, and at other times with it. And even in the unlikely event that the solar system as a whole is at rest relative to the ether, the earth’s motion will still generate an ether wind as it travels around the sun, just as you feel the wind on your face when you stick your head out of the window of a moving car on a perfectly still day.
Michelson and Morley set themselves the challenge of measuring the speed of light at different times of the year. They and everyone else firmly expected that the speed would change over the course of a year, albeit by a tiny amount, because the earth (and along with it their experiment) should be constantly changing its speed relative to the ether. Using a technique called interferometry, the experiments were exquisitely sensitive, and Michelson and Morley gradually refined the technique over six years before publishing their results in 1887. The result was unequivocally negative. No difference in the speed of light in any direction and at any time of year was observed.
If the ether hypothesis is correct, this result is very hard to explain. Imagine, for example, that you decide to dive into a fast-flowing river and swim downstream. If you swim at 5 kilometers per hour through the water, and the river is flowing at 3 kilometers per hour, then relative to the bank you will be swimming along at 8 kilometers per hour. If you turn and swim back upstream, then relative to the bank you will be swimming at 2 kilometers per hour. Michelson and Morley’s experiment is entirely analogous: You, the swimmer, are the beam of light, the river is the ether through which the light is supposed to travel, and the riverbank is Michelson and Morley’s experimental apparatus, sat at rest on the earth’s surface. Now we can see why the Michelson-Morley result was such a surprise. It was as if you always travel at 5 kilometers per hour relative to the riverbank, irrespective of the river’s speed of flow and the direction in which you decide to swim.
So Michelson and Morley failed to detect the presence of an ether flowing through their apparatus. Here is the next challenge to our intuition: Given what we have seen so far, the bold thing to do might be to jettison the notion of the ether because its effects cannot be observed, just as we jettisoned the notion of absolute space in Chapter 1. As an aside, from a philosophical perspective the ether was always a rather ugly concept, since it would define a benchmark in the universe against which absolute motion could be defined in conflict with Galileo’s principle of relativity. Historically, it seems likely that this was Einstein’s personal view, because he appears to have been only vaguely aware of Michelson and Morley’s experimental results when he took the bold step of abandoning the ether in formulating his special theory of relativity in 1905. It is certainly the case, however, that philosophical niceties are not a reliable guide to the workings of nature and, in the final analysis, the most valid reason to reject the ether is that the experimental results do not require it.1
While the rejection of the ether may be aesthetically pleasing and supported by the experimental data, if we choose to take this plunge then we are certainly left with a serious problem: Maxwell’s equations make a very precise prediction for the speed of light but contain no information at all about relative to what that speed should be measured. Let us for a moment be bold, accept the equations at face value, and see where the intellectual journey leads. If we arrive at nonsense, then we can always backtrack and try another hypothesis, feeling satisfied that we have done some science. Maxwell’s equations predict that light always moves with a velocity of 299,792,458 meters per second, and there is no place to insert the velocity of the source of the light or the velocity of the receiver. The equations really do seem to assert that the speed of light will always be measured to be the same, no matter how fast the source and the receiver of the light are moving relative to each other. It seems that Maxwell’s equations are telling us that the speed of light is a constant of nature. This really is a bizarre assertion, so let us spend a little more time exploring its meaning.
Imagine that light is shining out from a flashlight. According to common sense, if we run fast enough we could in principle catch up with the front of the beam of light as it advances forward. Common sense might even suggest that we could jog alongside the front of the beam if we managed to run at the speed of light. But if we are to follow Maxwell’s equations to the letter, then no matter how fast we run, the beam still recedes away from us at a speed of 299,792,458 meters per second. If it did not, the speed of light would be different for the person running compared to the person holding the flashlight, contradicting Michelson and Morley’s experimental results and our assertion that the speed of light is a constant of nature, always the same number, irrespective of the motion of the source or the observer. We seem to have talked ourselves into a ridiculous position. Surely common sense would advise us to reject, or at least modify or reinterpret Maxwell’s equations: Perhaps they are only approximately correct. Now, that doesn’t sound like an unreasonable proposition, since the motion of any realistic experimental apparatus would cause only a tiny variation in the 300 million meters per second that appears in Maxwell’s equations. So tiny indeed that perhaps it would have remained undetected in Faraday’s experiments. The alternative is to accept the validity of Maxwell’s equations and the bizarre proposition that we can never catch up with a beam of light. Not only is that idea an outrage to our common sense, but the next chapter will reveal that it also implies that we should reject the very notion of absolute time.
Breaking our attachment to absolute time is just as difficult to grasp today as it was to the nineteenth-century scientists. We have a strong intuition in favor of absolute space and time that is very hard to break, but we should be clear that intuition is all it is. Moreover, Newton’s laws embrace these notions wholeheartedly and, even to this day, those laws underpin the work of many engineers. Back in the nineteenth century, Newton’s laws seemed untouchable. While Faraday was laying bare the workings of electricity and magnetism at the Royal Institution, Isambard Kingdom Brunel was driving the Great Western Railway from London to Bristol. Brunel’s iconic Clifton Suspension Bridge was completed in 1864, the same year that Maxwell achieved his magnificent synthesis of Faraday’s work and uncovered the secret of light. The Brooklyn Bridge opened eight years later, and by 1889 the Eiffel Tower had risen above the Paris skyline. All of the magnificent achievements of the age of steam were designed and built using the concepts laid down by Newton. Newtonian mechanics was clearly far from being abstract mathematical musing. The symbols of its success were rising across the face of the globe in an ever-expanding celebration of humanity’s mastery of the laws of nature. Imagine the consternation in the minds of the late nineteenth-century scientists when they were faced with Maxwell’s equations and their implicit attack on the very foundations of the Newtonian worldview. Surely there could be only one winner. Surely Newton and the notion of absolute time would reign victorious.
Nevertheless, the twentieth century dawned with the problem of the constant speed of light still casting dark clouds: Maxwell and Newton could not both be right. It took until 1905 and the work of a hitherto unknown physicist named Albert Einstein for it to be finally demonstrated that nature sides with Maxwell.