The Elegant Universe: Superstrings, Hidden Dimensions, and the Quest for the Ultimate Theory - Brian Greene (2010)
Part II. The Dilemma of Space, Time, and the Quanta
Chapter 3. Of Warps and Ripples
Through special relativity Einstein resolved the conflict between the "age-old intuition" about motion and the constancy of the speed of light. In short, the solution is that our intuition is wrong—it is informed by motion that typically is extremely slow compared to the speed of light, and such low speeds obscure the true character of space and time. Special relativity reveals their nature and shows them to differ radically from previous conceptions. Tinkering with our understanding of the foundations of space and time, though, was no small undertaking. Einstein soon realized that of the numerous reverberations following from the revelations of special relativity, one was especially profound: The dictum that nothing can outrun light proves to be incompatible with Newton's revered universal theory of gravity, proposed in the latter half of the seventeenth century. And so, while resolving one conflict, special relativity gave rise to another. After a decade of intense, sometimes tormented study, Einstein resolved the dilemma with his general theory of relativity. In this theory, Einstein once again revolutionized our understanding of space and time by showing that they warp and distort to communicate the force of gravity.
Newton's View of Gravity
Isaac Newton, born in 1642 in Lincolnshire, England, changed the face of scientific research by bringing the full force of mathematics to the service of physical inquiry. Newton's was such a monumental intellect that, for example, when he found that the mathematics required for some of his investigations did not exist, he invented it. Nearly three centuries would pass before the world would host a comparable scientific genius. Of Newton's numerous profound insights into the workings of the universe, the one that primarily concerns us here is his universal theory of gravity.
The force of gravity pervades everyday life. It keeps us and all of the objects around us fixed to the earth's surface; it keeps the air we breathe from escaping to outer space; it keeps the moon in orbit around the earth and it keeps the earth bound in orbit around the sun. Gravity dictates the rhythm of the cosmic dance that is tirelessly and meticulously executed by billions upon billions of cosmic inhabitants, from asteroids to planets to stars to galaxies. More than three centuries of Newton's influence causes us to take for granted that a single force—gravity—is responsible for this wealth of terrestrial and extraterrestrial happenings. But before Newton there was no understanding that an apple falling to earth from a tree bore witness to the same physical principle that keeps the planets revolving around the sun. With an audacious step in the service of scientific hegemony, Newton united the physics governing both heaven and earth and declared the force of gravity to be the invisible hand at work in each realm.
Newton's view of gravity might be called the great equalizer. He declared that absolutely everything exerts an attractive gravitational force on absolutely everything else. Regardless of physical composition, everything exerts as well as feels the force of gravity. Based on a close study of Johannes Kepler's analysis of planetary motion, Newton deduced that the strength of the gravitational attraction between two bodies depends on precisely two things: the amount of stuff composing each of the bodies and the distance between them. "Stuff" means matter—this comprises the total number of protons, neutrons, and electrons, which in turn determines the mass of the object. Newton's universal theory of gravity asserts that the strength of attraction between two objects is larger for larger-mass objects and smaller for smaller-mass objects; it also asserts that the strength of attraction is larger for smaller separations between the objects and smaller for larger separations.
Newton went much further than this qualitative description and wrote down equations that quantitatively describe the strength of the gravitational force between two objects. In words, these equations state that the gravitational force between two bodies is proportional to the product of their masses and inversely proportional to the square of the distance between them. This "law of gravity" can be used to predict the motion of planets and comets around the sun, the moon about the earth, and rockets heading off for planetary explorations, as well as more earthbound applications such as baseballs flying through the air and divers spiraling poolward from springboards. The agreement between the predictions and the actual observed motion of such objects is spectacular. This success gave Newton's theory unequivocal support until the early part of the twentieth century. Einstein's discovery of special relativity, however, raised what proved to be an insurmountable obstacle for Newton's theory.
The Incompatibility of Newtonian Gravity and Special Relativity
A central feature of special relativity is the absolute speed barrier set by light. It is important to realize that this limit applies not only to material objects but also to signals and influences of any kind. There is simply no way to communicate information or a disturbance from one place to another at faster than light speed. Of course, the world is full of ways for transmitting disturbances at slower than the speed of light. Your speech and all other sounds, for example, are carried by vibrations that travel at about 700 miles per hour through air, a feeble rate compared with light's 670 million miles per hour. This speed difference becomes obvious when you watch a baseball game, from seats that are far from home plate. When a batter hits the ball, the sound reaches you moments after you see the ball being hit. A similar thing happens in a thunderstorm. Although lightning and thunder are produced simultaneously, you see the lightning before hearing the thunder. Again, this reflects the substantial speed difference between light and sound. The success of special relativity informs us that the reverse situation, in which some signal reaches us before the light it emits, is just not possible. Nothing outruns photons.
Here's the rub. In Newton's theory of gravity, one body exerts a gravitational pull on another with a strength determined solely by the mass of the objects involved and the magnitude of their separation. The strength has nothing to do with how long the objects have been in each other's presence. This means that if their mass or their separation should change, the objects will, according to Newton, immediately feel a change in their mutual gravitational attraction. For instance, Newton's theory of gravity claims that if the sun were suddenly to explode, the earth—some 93 million miles away—would instantaneously suffer a departure from its usual elliptical orbit. Even though it would take light from the explosion eight minutes to travel from the sun to the earth, in Newton's theory knowledge that the sun had exploded would be instantaneously transmitted to the earth through the sudden change in the gravitational force governing its motion.
This conclusion is in direct conflict with special relativity, since the latter ensures that no information can be transmitted faster than the speed of light—instantaneous transmission violates this precept maximally.
In the early part of the twentieth century, therefore, Einstein realized that the tremendously successful Newtonian theory of gravity was in conflict with his special theory of relativity. Confident in the veracity of special relativity and notwithstanding the mountain of experimental support for Newton's theory, Einstein sought a new theory of gravity compatible with special relativity. This ultimately led him to the discovery of general relativity, in which the character of space and time again went through a remarkable transformation.
Einstein's Happiest Thought
Even before the discovery of special relativity, Newton's theory of gravity was lacking in one important respect. Although it can be used to make highly accurate predictions about how objects will move under the influence of gravity, it offers no insight into what gravity is. That is, how is it that two bodies that are physically separate from another, possibly hundreds of millions of miles apart if not more, nonetheless influence each other's motion? By what means does gravity execute its mission? This is a problem of which Newton himself was well aware. In his own words,
It is inconceivable, that inanimate brute matter, should, without the mediation of something else, which is not material, operate upon and affect other matter without mutual contact. That Gravity should be innate, inherent and essential to matter so that one body may act upon another at a distance thro' a vacuum without the mediation of anything else, by and through which their action and force may be conveyed, from one to another, is to me so great an absurdity that I believe no Man who has in philosophical matters a competent faculty of thinking can ever fall into it. Gravity must be caused by an agent acting constantly according to certain laws; but whether this agent be material or immaterial, I have left to the consideration of my readers.1
That is, Newton accepted the existence of gravity and went on to develop equations that accurately describe its effects, but he never offered any insight into how it actually works. He gave the world an "owner's manual" for gravity which delineated how to "use" it—instructions that physicists, astronomers, and engineers have exploited successfully to plot the course of rockets to the moon, Mars, and other planets in the solar system; to predict solar and lunar eclipses; to predict the motion of comets, and so on. But he left the inner workings—the contents of the "black box" of gravity—a complete mystery. When you use your CD player or your personal computer, you may find yourself in a similar state of ignorance regarding how it works internally. So long as you know how to operate the equipment neither you nor anyone else needs to know how it accomplishes the tasks you set for it. But if your CD player or personal computer breaks, its repair relies crucially on knowledge of its internal workings. Similarly, Einstein realized that hundreds of years of experimental confirmation notwithstanding, special relativity implied that in some subtle way Newton's theory was "broken" and that its repair required coming to grips with the question of the true and full nature of gravity.
In 1907, while pondering these issues at his desk in the patent office in Bern, Switzerland, Einstein had the central insight that, through fits and starts, would eventually lead him to a radically new theory of gravity—an approach that would not merely fill in the gap in Newton's theory, but, rather, would completely reformulate thinking about gravity and, of utmost importance, would do so in a manner fully consistent with special relativity.
The insight Einstein had is relevant for a question that may have troubled you in Chapter 2. There we emphasized that we were interested in understanding how the world appears to individuals undergoing constant-velocity relative motion. By carefully comparing the observations of such individuals, we found some dramatic implications for the nature of space and time. But what about individuals who are experiencing accelerated motion? The observations of such individuals will be more complicated to analyze than those of constant-velocity observers, whose motion is more serene, but nevertheless we can ask whether there is some way of taming this complexity and bringing accelerated motion squarely into our newfound understanding of space and time.
Einstein's "happiest thought" showed how to do so. To understand his insight, imagine the year is 2050, you are the FBI's chief explosives expert, and you have just received a frantic call to investigate what appears to be a sophisticated bomb planted in the heart of Washington, D.C. After rushing to the scene and examining the device, your worst nightmare is confirmed: The bomb is nuclear and of such powerful design that even if it were buried deeply in the earth's crust or submerged in an ocean's depth, the damage from its blast would be devastating. After gingerly studying the bomb's detonation mechanism you realize that there is no hope to disarm it and, furthermore, you see that it has a novel booby-trap feature. The bomb is mounted on a scale. Should the reading on the scale deviate from its present value by more than 50 percent, the bomb will detonate. According to the timing mechanism, you see that you have but one week and counting. The fate of millions of people rests on your shoulders—what do you do?
Well, having determined that there is no safe place anywhere on or in the earth to detonate the device, you appear to have only one option: You must launch the device into the depths of outer space where its explosion will cause no damage. You present this idea to a meeting of your team at the FBI and almost immediately your plan is dashed by a young assistant. "There is a serious problem with your plan," your assistant Isaac begins. "As the device gets farther from the earth, its weight will decrease, since its gravitational attraction with the earth will diminish. This means that the reading on the scale inside the device will decrease, causing detonation well before reaching the safety of deep space." Before you have time to fully contemplate this criticism, another young assistant pipes up: "In fact, come to think of it, there is even another problem," your assistant Albert says. "This problem is as important as Isaac's objection but somewhat more subtle, so bear with me as I explain it." Wanting a moment to think through Isaac's objection, you try to hush Albert, but as usual, once he begins there is no stopping him.
"In order to launch the device into outer space we will have to mount it on a rocket. As the rocket accelerates upward in order to penetrate outer space, the reading on the scale will increase, again causing the device to detonate prematurely. You see, the base of the bomb—which rests on the scale—will push harder on the scale than when the device is at rest in the same way that your body is squeezed back into the seat of an accelerating car. The bomb will 'squeeze' the scale just as your back squeezes the cushion in the car seat. When a scale is squeezed, of course, its reading increases—and this will cause the bomb to detonate if the resulting increase is more than 50 percent."
You thank Albert for his comment but, having tuned out his explanation to mentally confirm Isaac's remark, you dejectedly proclaim that it takes only one fatal blow to kill an idea, and Isaac's obviously correct observation has definitively done that. Feeling somewhat hopeless you ask for new suggestions. At that moment, Albert has a stunning revelation: "On second thought," he continues, "I do not think that your idea is dead at all. Isaac's observation that gravity diminishes as the device is lifted into space means that the reading on the scale will go down. My observation that the upward acceleration of the rocket will cause the device to push harder against the scale means that the reading will go up. Taken together, this means that if we carefully adjust the precise moment-to-moment acceleration of the rocket as it moves upward, these two effects can cancel each other out! Specifically, in the early stages of liftoff, when the rocket still feels the full force of the earth's gravity, it can accelerate, just not too severely, so that we stay within the 50 percent window. As the rocket gets farther and farther from the earth—and therefore feels the earth's gravity less and less—we need to increase its upward acceleration to compensate. The increase in the reading from upward acceleration can exactly equal the decrease in the reading from the diminishing gravitational attraction, so, in fact, we can keep the actual reading on the scale from changing at all!"
Albert's suggestion slowly begins to make sense. "In other words," you respond, "an upward acceleration can provide a stand-in or a substitute for gravity. We can imitate the effect of gravity through suitably accelerated motion."
"Exactly," responds Albert.
"So," you continue, "we can launch the bomb into space and by judiciously adjusting the acceleration of the rocket we can ensure that the reading on the scale does not change, thus avoiding detonation until it is a safe distance from earth." And so by playing off gravity and accelerated motion—using the precision of twenty-first-century rocket science—you are able to stave off disaster.
The recognition that gravity and accelerated motion are profoundly interwoven is the key insight that Einstein had one happy day in the Bern patent office. Although the bomb experience highlights the essence of his idea, it is worth rephrasing it in a framework closer to that of Chapter 2. For this purpose, recall that if you are put into a sealed, windowless compartment that is not accelerating, there is no way for you to determine your speed. The compartment looks the same and any experiments you do yield identical results regardless of how fast you are moving. More fundamentally, without outside benchmarks for comparison there is no way that a velocity can even be assigned to your state of motion. On the other hand, if you are accelerating, then even with your perceptions limited to the confines of your sealed compartment, you will feel a force on your body. For instance, if your forward-facing chair is bolted to the floor and your compartment is being accelerated forward, you will feel the force of your seat on your back just as with the car described by Albert. Similarly, if your compartment is being accelerated upward you will feel the force of the floor on your feet. Einstein's realization was that within the confines of your tiny compartment, you will not be able to distinguish these accelerated situations from ones without acceleration but with gravity: When their magnitudes are judiciously adjusted, the force you feel from a gravitational field or from accelerated motion are indistinguishable. If your compartment is placidly sitting upright on the earth's surface, you will feel the familiar force of the floor on your feet, just as in the scenario of upward acceleration; this is exactly the same equivalence Albert exploited in his solution for launching the terrorist bomb into space. If your compartment is resting on its back end you will feel the force of your seat on your back (preventing you from falling), just as when you were accelerating horizontally. Einstein called the indistinguishability between accelerated motion and gravity the equivalence principle. It plays a central role in general relativity.2
This description shows that general relativity finishes a job initiated by special relativity. Through its principle of relativity, the special theory of relativity declares a democracy of observational vantage points: the laws of physics appear identical to all observers undergoing constant-velocity motion. But this is limited democracy indeed, for it excludes an enormous number of other viewpoints—those of individuals who are accelerating. Einstein's 1907 insight now shows us how to embrace all points of view—constant velocity and accelerating—within one egalitarian framework. Since there is no difference between an accelerated vantage point without a gravitational field and a nonaccelerated vantage point with a gravitational field, we can invoke the latter perspective and declare that all observers, regardless of their state of motion, may proclaim that they are stationary and "the rest of the world is moving by them," so long as they include a suitable gravitational field in the description of their own surroundings. In this sense, through the inclusion of gravity, general relativity ensures that all possible observational vantage points are on equal footing. (As we shall see later, this means that distinctions between observers in Chapter 2 that relied on accelerated motion—as when George chased after Gracie by turning on his jet-pack and aged less than she—admit an equivalent description without acceleration, but with gravity.)
This deep connection between gravity and accelerated motion is certainly a remarkable realization, but why did it make Einstein so happy? The reason, simply put, is that gravity is mysterious. It is a grand force permeating the life of the cosmos, but it is elusive and ethereal. On the other hand, accelerated motion, although somewhat more complicated than constant-velocity motion, is concrete and tangible. By finding a fundamental link between the two, Einstein realized that he could use his understanding of motion as a powerful tool toward gaining a similar understanding of gravity. Putting this strategy into practice was no small task, even for the genius of Einstein, but ultimately this approach bore the fruit of general relativity. Achieving this end required that Einstein forge a second link in the chain uniting gravity and accelerated motion: the curvature of space and time, to which we now turn.
Acceleration and the Warping of Space and Time
Einstein worked on the problem of understanding gravity with extreme, almost obsessive, intensity. About five years after his happy revelation in the Bern patent office, he wrote to the physicist Arnold Sommerfeld, "I am now working exclusively on the gravity problem…. [O]ne thing is certain—that never in my life have I tormented myself anything like this…. Compared to this problem the original [i.e., special] relativity theory is child's play."3
He appears to have made the next key breakthrough, a simple yet subtle consequence of applying special relativity to the link between gravity and accelerated motion, in 1912. To understand this step in Einstein's reasoning it is easiest to focus, as apparently he did, on a particular example of accelerated motion.4 Recall that an object is accelerating if either the speed or the direction of its motion changes. For simplicity we will focus on accelerated motion in which only the direction of our object's motion changes while its speed stays fixed. Specifically, we consider motion in a circle such as what one experiences on the Tornado ride in an amusement park. In case you have never tested the stability of your constitution on this ride, you stand with your back against the inside of a circular Plexiglas structure that spins at a high speed. Like all accelerated motion, you can feel this motion—you feel your body being pulled radially away from the ride's center and you feel the circular wall of Plexiglas pressing on your back, keeping you moving in a circle. (In fact, although not relevant for the present discussion, the spinning motion "pins" your body to the Plexiglas with such a force that when the ledge on which you are standing drops away you do not slip downward.) If the ride is extremely smooth and you close your eyes, the pressure of the ride on your back—like the support of a bed—can almost make you feel that you are lying down. The "almost" comes from the fact that you still feel ordinary "vertical" gravity, so your brain cannot be fully fooled. But if you were to ride the Tornado in outer space, and if it were to spin at just the right rate, it would feel just like lying in a stationary bed on earth. Moreover, were you to "get up" and walk along the interior of the spinning Plexiglas, your feet would press against it just as they do against an earthbound floor. In fact, space stations are designed to spin in this manner to create an artificial feeling of gravity in outer space.
Having used the accelerated motion of the spinning Tornado to imitate gravity, we can now follow Einstein and set out to see how space and time appear to someone on the ride. His reasoning, adapted to this situation, went as follows. We stationary observers can easily measure the circumference and the radius of the spinning ride. For instance, to measure the circumference we can carefully lay out a ruler—head to tail—alongside the ride's spinning girth; for its radius we can similarly use the head-to-tail method working our way from the central axle of the ride to its outer rim. As we anticipate from high-school geometry, we find that their ratio is two times the number pi—about 6.28—just as it is for any circle drawn on a flat sheet of paper. But what do things look like from the perspective of someone on the ride itself?
To find out, we ask Slim and Jim, who are currently enjoying a spin on the Tornado, to take a few measurements for us. We toss one of our rulers to Slim, who sets out to measure the circumference of the ride, and another to Jim, who sets out to measure the radius. To get the clearest perspective, let's take a bird's-eye view of the ride, as in Figure 3.1. We have adorned this snapshot of the ride with an arrow that indicates the momentary direction of motion at each point. As Slim begins to measure the circumference, we immediately see from our bird's-eye perspective that he is going to get a different answer than we did. As he lays the ruler out along the circumference, we notice that the ruler's length is shortened. This is nothing but the Lorentz contraction discussed in Chapter 2, in which the length of an object appears shortened along the direction of its motion. A shorter ruler means that he will have to lay it out—head to tail—more times to traverse the whole circumference. Since he still considers the ruler to be one foot long (since there is no relative motion between Slim and his ruler, he perceives it as having its usual length of one foot), this means that Slim will measure a longer circumference than did we. (If this seems paradoxical, you might find endnote 5 helpful.)
What about the radius? Well, Jim also uses the head-to-tail method to find the length of a radial strut, and from our bird's-eye view we see that he is going to find the same answer as we did. The reason is that the ruler is not pointing along the instantaneous direction of the motion of the ride (as it is when measuring the circumference). Instead, it is pointed at a ninety-degree angle to the motion, and therefore it is not contracted along its length. Jim will therefore find exactly the same radial length as we did.
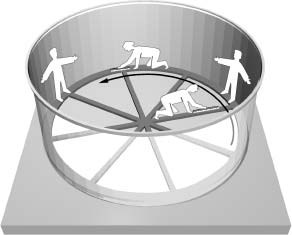
Figure 3.1 Slim's ruler is contracted, since it lies along the direction of the ride's motion. But Jim's ruler lies along a radial strut, perpendicular to the direction of the ride's motion, and therefore its length is not contracted.
But now, when Slim and Jim calculate the ratio of the circumference of the ride to its radius they will get a number that is larger than our answer of two times pi, since the circumference is longer but the radius is the same. This is weird. How in the world can something in the shape of a circle violate the ancient Greek realization that for any circle this ratio is exactly two times pi?
Here is Einstein's explanation. The ancient Greek result holds true for circles drawn on a flat surface. But just as the warped or curved mirrors in an amusement park fun-house distort the normal spatial relationships of your reflection, if a circle is drawn on a warped or curved surface, its usual spatial relationships will also be distorted: the ratio of its circumference to its radius will generally not be two times pi.
For instance, Figure 3.2 compares three circles whose radii are identical. Notice, however, that their circumferences are not the same. The circumference of the circle in (b), drawn on the curved surface of a sphere, is less than the circumference of the circle drawn on the flat surface in (a), even though they have the same radius. The curved nature of the sphere's surface causes the radial lines of the circle to converge toward each other slightly, resulting in a small decrease in the circle's circumference. The circumference of the circle in (c), again drawn on a curved surface—a saddle shape—is greater than that drawn on a flat surface; the curved nature of the saddle's surface causes the radial lines of the circle to splay outward from each other slightly, resulting in a small increase in the circle's circumference. These observations imply that the ratio of the circumference to the radius of the circle in (b) will be less than two times pi, while the same ratio in (c) will be greater than two times pi. But this deviation from two times pi, especially the larger value found in (c), is just what we found for the spinning Tornado ride. This led Einstein to propose an idea—the curving of space—as an explanation for the violation of "ordinary," Euclidean geometry. The flat geometry of the Greeks, taught to schoolchildren for thousands of years, simply does not apply to someone on the spinning ride. Rather, its curved space generalization as schematically drawn in part (c) of Figure 3.2 takes its place.5
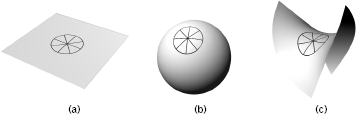
Figure 3.2 A circle drawn on a sphere (b) has a shorter circumference than one drawn on a flat sheet of paper (a), while a circle drawn on the surface of a saddle (c) has a longer circumference, even though they all have the same radius.
And so Einstein realized that the familiar geometrical spatial relationships codified by the Greeks, relationships that pertain to "flat" space figures like a circle on a flat table, do not hold from the perspective of an accelerated observer. Of course, we have discussed only one particular kind of accelerated motion, but Einstein showed that a similar result—the warping of space—holds in all instances of accelerated motion.
In fact, accelerated motion not only results in a warping of space, it also results in an analogous warping of time. (Historically, Einstein first focused on the warping of time and subsequently realized the importance of the warping of space.6) On one level, it should not be too surprising that time is also affected, since we have already seen in Chapter 2 that special relativity articulates a union between space and time. This merger was summarized by the poetic words of Minkowski, who during a lecture on special relativity in 1908 said, "Henceforward space on its own and time on its own will decline into mere shadows, and only a kind of union between the two will preserve its independence."7 In more down-to-earth but similarly imprecise language, by knitting space and time together into the unified structure of spacetime, special relativity declares, "What's true for space is true for time." But this raises a question: Whereas we can picture warped space by its having a curved shape, what do we really mean by warped time?
To get a feel for the answer, let's once again impose upon Slim and Jim on the Tornado ride and ask them to carry out the following experiment. Slim will stand with his back against the ride, at the far end of one of the ride's radial struts, while Jim will slowly crawl toward him along the strut, starting from the ride's center. Every few feet, Jim will stop his crawling and the two brothers are to compare the readings on their watches. What will they find? From our stationary, bird's-eye perspective, we can again predict the answer: Their watches will not agree. We come to this conclusion because we realize that Slim and Jim are travelling at different speeds—on the Tornado ride, the farther out along a radial strut you are, the farther you must travel to complete one rotation, and therefore the faster you must go. But from special relativity, the faster you go, the slower your watch ticks, and hence we realize that Slim's watch will tick more slowly than Jim's. Furthermore, Slim and Jim will find that, as Jim gets closer to Slim, the ticking rate of Jim's watch will slow down, approaching that of Slim's. This reflects the fact that as Jim gets farther out along the strut, his circular speed increases toward that of Slim.
We conclude that to observers on the spinning ride, such as Slim and Jim, the rate of passage of time depends upon their precise position—in this case, their distance from the center of the ride. This is an illustration of what we mean by warped time: Time is warped if its rate of passage differs from one location to another. And of particular importance to our present discussion, Jim will also notice something else as he crawls out along the strut. He will feel an increasingly strong outward pull because not only does speed increase, but his acceleration increases as well, the farther he is from the spinning ride's center. On the Tornado ride, then, we see that greater acceleration is tied up with slower clocks—that is, greater acceleration results in a more significant warping of time.
These observations took Einstein to the final leap. Since he had already shown gravity and accelerated motion to be effectively indistinguishable, and since he now had shown that accelerated motion is associated with the warping of space and time, he made the following proposal for the innards of the "black box" of gravity—the mechanism by which gravity operates. Gravity, according to Einstein, is the warping of space and time. Let's see what this means.
The Basics of General Relativity
To get a feel for this new view of gravity, let's consider the prototypical situation of a planet, such as the earth, revolving around a star, such as the sun. In Newtonian gravity the sun keeps the earth in orbit with an unidentified gravitational "tether" that somehow instantaneously reaches out across vast distances of space and grabs hold of the earth (and, similarly, the earth reaches out and grabs hold of the sun). Einstein provided a new conception of what actually happens. It will aid in our discussion of Einstein's approach to have a concrete visual model of spacetime that we can conveniently manipulate. To do so, we will simplify things in two ways. First, for the moment, we will ignore time and focus solely on a visual model of space. We will reincorporate time in our discussion shortly. Second, in order to allow us to draw and manipulate visual images on the pages of this book, we will often refer to a two-dimensional analog of three-dimensional space. Most of the insight we gain from thinking in terms of this lower-dimensional model is directly applicable to the physical three-dimensional setting, so the simpler model provides a powerful pedagogical device.
In Figure 3.3, we make use of these simplifications and draw a two-dimensional model of a spatial region of our universe. The grid-like structure indicates a convenient means of specifying positions just as a street grid gives a means of specifying locations in a city. In a city, of course, one gives an address by specifying a location on the two-dimensional street grid and also giving a location in the vertical direction, such as a floor number. It is the latter information, location in the third spatial dimension, that our two-dimensional analogy suppresses for visual clarity.

Figure 3.3 A schematic representation of flat space.
In the absence of any matter or energy, Einstein envisioned that space would be flat. In our two-dimensional model, this means that the "shape" of space should be like the surface of a smooth table, as drawn in Figure 3.3. This is the image of our spatial universe commonly held for thousands of years. But what happens to space if a massive object like the sun is present? Before Einstein the answer was nothing;space (and time) were thought to provide an inert theater, merely setting the stage on which the events of the universe play themselves out. The chain of Einstein's reasoning that we have been following, however, leads to a different conclusion.
A massive body like the sun, and indeed any body, exerts a gravitational force on other objects. In the example of the terrorist bomb, we learned that gravitational forces are indistinguishable from accelerated motion. In the example of the Tornado ride, we learned that a mathematical description of accelerated motion requires the relations of curved space. These links between gravity, accelerated motion, and curved space led Einstein to the remarkable suggestion that the presence of mass, such as the sun, causes the fabric of space around it to warp, as shown in Figure 3.4. A useful, and oft-quoted, analogy is that much like a rubber membrane on which a bowling ball has been placed, the fabric of space becomes distorted due to the presence of a massive object like the sun. According to this radical proposal, space is not merely a passive forum providing the arena for the events of the universe; rather, the shape of space responds to objects in the environment.

Figure 3.4 A massive body like the sun causes the fabric of space to warp, somewhat like the effect of a bowling ball placed on a rubber sheet.
This warping, in turn, affects other objects moving in the vicinity of the sun, as they now must traverse the distorted spatial fabric. Using the rubber membrane-bowling ball analogy, if we place a small ball-bearing on the membrane and set it off with some initial velocity, the path it will follow depends on whether or not the bowling ball is sitting in the center. If the bowling ball is absent, the rubber membrane will be flat and the ball bearing will travel along a straight line. If the bowling ball is present and thereby warps the membrane, the ball bearing will travel along a curved path. In fact, ignoring friction, if we set the ball bearing moving with just the right speed in just the right direction, it will continue to move in a recurring curved path around the bowling ball—in effect, it will "go into orbit." Our language presages the application of this analogy to gravity.
The sun, like the bowling ball, warps the fabric of space surrounding it, and the earth's motion, like that of the ball bearing, is determined by the shape of the warp. The earth, like the ball bearing, will move in orbit around the sun if its speed and orientation have suitable values. This effect on the motion of the earth is what we normally would refer to as the gravitational influence of the sun, and is illustrated in Figure 3.5. The difference, now, is that unlike Newton, Einstein has specified the mechanism by which gravity is transmitted: the warping of space. In Einstein's view, the gravitational tether holding the earth in orbit is not some mysterious instantaneous action of the sun; rather, it is the warping of the spatial fabric caused by the sun's presence.

Figure 3.5 The earth is kept in orbit around the sun because it rolls along a valley in the warped spatial fabric. In more precise language, it follows a "path of least resistance" in the distorted region around the sun.
This picture allows us to understand the two essential features of gravity in a new way. First, the more massive the bowling ball, the greater the distortion it causes in the rubber membrane; similarly, in Einstein's description of gravity the more massive an object is, the greater the distortion it causes in the surrounding space. This implies that the more massive an object, the greater the gravitational influence it can exert on other bodies, precisely in accord with our experiences. Second, just as the distortion of the rubber membrane due to the bowling ball gets smaller as one gets farther from it, the amount of spatial warping due to a massive body such as the sun decreases as one's distance from it increases. This, again, jibes with our understanding of gravity, whose influence becomes weaker as the distance between objects becomes larger.
An important point to note is that the ball bearing itself warps the rubber membrane, although only slightly. Similarly, the earth, being a massive body in its own right, also warps the fabric of space, although far less than the sun. This is how, in the language of general relativity, the earth keeps the moon in orbit, and it is also how the earth keeps each of us bound to its surface. As a skydiver plunges earthward, he or she is sliding down a depression in the spatial fabric caused by the earth's mass. Moreover, each of us—like any massive object—also warps the spatial fabric in close proximity to our bodies, although the comparatively small mass of a human body makes this a minuscule indentation.
In summary then, Einstein fully agreed with Newton's statement that "Gravity must be caused by an agent" and rose to Newton's challenge in which the identity of the agent was left "to the consideration of my readers." The agent of gravity, according to Einstein, is the fabric of the cosmos.
A Few Caveats
The rubber membrane-bowling ball analogy is valuable because it gives us a visual image with which we can grasp tangibly what we mean by a warp in the spatial fabric of the universe. Physicists often use this and similar analogies to guide their own intuition regarding gravitation and curvature. However, its usefulness notwithstanding, the rubber membrane-bowling ball analogy is not perfect and for clarity we call attention to a few of its shortcomings.
First, when the sun causes the fabric of space around it to warp this is not due to its "being pulled downward" by gravity as in the case of the bowling ball, which warps the rubber membrane because it is pulled earthward by gravity. In the case of the sun, there is no other object to "do the pulling." Instead, Einstein has taught us that the warping of space is gravity. The mere presence of an object with mass causes space to respond by warping. Similarly, the earth is not kept in orbit because the gravitational pull of some other external object guides it along the valleys in the warped spatial environment, as occurs for a ball bearing on the warped rubber membrane. Instead, Einstein showed that objects move through space (spacetime, more precisely) along the shortest possible paths—the "easiest possible paths" or the "paths of least resistance." If the space is warped, such paths will be curved. And so, although the rubber membrane-bowling ball model provides a good visual analogy of how an object such as the sun warps the space around it and thereby influences the motion of other bodies, the physical mechanism by which these distortions occur is totally different. The former appeals to our intuition about gravity in the traditional Newtonian framework, whereas the latter expresses a reformulation of gravity in terms of curved space.
A second shortcoming of the analogy stems from the rubber membrane's being two-dimensional. In reality, although harder to visualize, the sun (and all other massive objects) actually warps the three-dimensional space surrounding it. Figure 3.6 is a rough attempt to depict this; all of the space surrounding the sun—"below," "on the sides," on "top"—suffers the same kind of distortion, and Figure 3.6 schematically shows a partial sampling. A body, like the earth, travels through the three-dimensional warped spatial environment caused by the sun's presence. You may find this figure troubling—why doesn't the earth slam into the "vertical part" of curved space in the image? Bear in mind, though, that space, unlike the rubber membrane, is not a solid barrier. Instead, the warped grids in the image are but a couple of thin slices through the full three-dimensional warped space in which you, the earth, and everything else are immersed fully and move freely. Perhaps you find that this only makes the problem seem worse: Why don't we feel space if we are immersed within its fabric? But we do. We feel gravity, and space is the medium by which the gravitational force is communicated. As the eminent physicist John Wheeler has often said in describing gravity, "mass grips space by telling it how to curve, space grips mass by telling it how to move."8
A third, related shortcoming of the analogy is that we have suppressed the time dimension. We have done this for visual clarity because, notwithstanding the declaration of special relativity that we should think of the time dimension on par with the three familiar spatial dimensions, it is significantly harder to "see" time. But, as illustrated by the example of the Tornado ride, acceleration—and hence gravity—warps both space and time. (In fact, the mathematics of general relativity shows that in the case of a relatively slow-moving body like the earth revolving around a typical star like the sun, the warping of time actually has a far more significant impact on the earth's motion than does the warping of space.) We will return to a discussion of the warping of time after the next section.

Figure 3.6 A sampling of the warped three-dimensional space surrounding the sun.
Important as these three caveats are, so long as you hold them in the back of your mind, it is perfectly acceptable to invoke the warped-space image provided by the bowling ball on the rubber membrane as an intuitive summary of Einstein's new view of gravity.
Conflict Resolution
By introducing space and time as dynamic players, Einstein provided a clear conceptual image of how gravity works. The central question, though, is whether this reformulation of the gravitational force resolves the conflict with special relativity that afflicts Newton's theory of gravity. It does. Again, the rubber membrane analogy gives the essential idea. Imagine that we have a ball bearing rolling in a straight line along the flat membrane in the absence of the bowling ball. As we place the bowling ball on the membrane the motion of the ball bearing will be affected, but not instantaneously. If we were to film this sequence of events and view it in slow motion we would see that the disturbance caused by the introduction of the bowling ball spreads like ripples in a pond and eventually reaches the position of the ball bearing. After a short time, transitory oscillations along the rubber surface would settle down, leaving us with a static warped membrane.
The same is true for the fabric of space. When no mass is present, space is flat, and a small object will blissfully be at rest or will travel at a constant velocity. If a large mass comes on the scene, space will warp—but as in the case of the membrane, the distortion will not be instantaneous. Rather, it will spread outward from the massive body, ultimately settling down into a warped shape that communicates the gravitational pull of the new body. In our analogy, disturbances to the rubber membrane travel along its extent at a speed dictated by its particular material composition. In the real setting of general relativity, Einstein was able to calculate how fast disturbances to the fabric of the universe travel and he found that they travel at precisely the speed of light. This means, for instance, that in the hypothetical example discussed earlier in which the demise of the sun affects the earth by virtue of changes in their mutual gravitational attraction, the influence will not be instantaneously communicated. Rather, as an object changes its position or even blows apart, it causes a change in the distortion of the spacetime fabric that spreads outward at light speed, precisely in keeping with the cosmic speed limit of special relativity. Thus, we on earth would visually learn of the sun's destruction at the same moment that we would feel the gravitational consequences—about eight minutes after it explodes. Einstein's formulation thereby resolves the conflict; gravitational disturbances keep pace with, but do not outrun, photons.
The Warping of Time, Revisited
Illustrations such as those of Figures 3.2, 3.4, and 3.6 capture the essence of what "warped space" means. A warp distorts the shape of space. Physicists have invented analogous images to try to convey the meaning of "warped time," but they are significantly more difficult to decipher, so we will not introduce them here. Instead, let's follow up the example of Slim and Jim on the Tornado ride, and try to get a sense of the experience of gravitationally induced warped time.
To do so, we revisit George and Gracie, no longer in the deep darkness of empty space, but floating near the outskirts of the solar system. They are still each wearing large digital clocks on their space suits that are initially synchronized. To keep things simple, we ignore the effects of the planets and consider only the gravitational field of the sun. Let's further imagine that a spaceship hovering near George and Gracie has reeled out a long cable extending all the way down to the vicinity of the sun's surface. George uses this cable to slowly lower himself toward the sun. As he does so, he periodically stops so that he and Gracie can compare the rate at which time is elapsing on their clocks. The warping of time predicted by Einstein's general relativity implies that George's clock will run slower and slower compared with Gracie's as the gravitational field he experiences gets stronger and stronger. That is, the closer he gets to the sun the slower his clock will run. It is in this sense that gravity distorts time as well as space.
You should note that unlike the case in Chapter 2 in which George and Gracie were in empty space moving relative to each other with constant velocity, in the present setting there is no symmetry between them. George, unlike Gracie, feels the force of gravity getting stronger and stronger—he has to hold the cable tighter and tighter as he gets closer to the sun to avoid being pulled in. Each of them agrees that George's clock is running slow. There is no "equally valid perspective" that exchanges their roles and reverses this conclusion. This is, in fact, what we found in Chapter 2 when George experienced an acceleration by turning on his jet-pack to catch up with Gracie. The acceleration George felt resulted in his clock definitively running slow relative to Gracie's. Since we now know that feeling accelerated motion is the same as feeling a gravitational force, the present situation of George on the cable involves the same principle, and once again we see that George's clock, and everything else in his life, runs in slow motion compared with Gracie's.
In a gravitational field such as that at the surface of an ordinary star like the sun, the slowing of clocks is quite small. If Gracie stays put at a billion miles from the sun, then when George has climbed to within a few miles of its surface, the rate of ticking of his clock will be about 99.9998 percent of Gracie's. Slower, but not by much.9 If, however, George lowered himself on a cable so that he hovered just above the surface of a neutron star whose mass, roughly equal to that of the sun, is crushed to a density some million billion times that of solar density, the larger gravitational field would cause his clock to tick at about 76 percent of the rate of Gracie's. Stronger gravitational fields, such as those just outside a black hole (as discussed below), cause the flow of time to slow even further; stronger gravitational fields cause a more severe warping of time.
Experimental Verification of General Relativity
Most people who study general relativity are captivated by its aesthetic elegance. By replacing the cold, mechanistic Newtonian view of space, time, and gravity with a dynamic and geometric description involving curved spacetime, Einstein wove gravity into the basic fabric of the universe. Rather than being imposed as an additional structure, gravity becomes part and parcel of the universe at its most fundamental level. Breathing life into space and time by allowing them to curve, warp, and ripple results in what we commonly refer to as gravity.
Aesthetics aside, the ultimate test of a physical theory is its ability to explain and predict physical phenomena accurately. Since its inception in the late 1600s until the beginning of this century, Newton's theory of gravity passed this test with flying colors. Whether applied to balls thrown up in the air, objects dropped from leaning towers, comets whirling around the sun, or planets going about their solar orbits, Newton's theory provides extremely accurate explanations of all observations as well as predictions that have been verified innumerable times in a wealth of situations. The motivation for questioning this experimentally successful theory, as we have emphasized, was its property of instantaneous transmission of the gravitational force, in conflict with special relativity.
The effects of special relativity, although central to a fundamental understanding of space, time, and motion, are extremely small in the slow-velocity world we typically inhabit. Similarly, the deviations between Einstein's general relativity—a theory of gravity compatible with special relativity—and Newton's theory of gravity are also extremely small in most common situations. This is both good and bad. It is good because any theory purporting to supplant Newton's theory of gravity had better closely agree with it when applied in those arenas in which Newton's theory has been experimentally verified. It is bad because it makes it difficult to adjudicate between the two theories experimentally. Distinguishing between Newton's and Einstein's theories requires extremely precise measurements applied to experiments that are very sensitive to the ways in which the two theories differ. If you throw a baseball, Newtonian and Einsteinian gravity can be used to predict where it will land, and the answers will be different, but the differences will be so slight that they are generally beyond our capacity to detect experimentally. A more clever experiment is called for, and Einstein suggested one.10
We see stars at night, but of course they are also there during the day. We usually don't see them because their distant, pinpoint light is overwhelmed by the light emitted by the sun. During a solar eclipse, however, the moon temporarily blocks the light of the sun and distant stars become visible. Nevertheless, the presence of the sun still has an effect. Light from some of the distant stars must pass close to the sun on the way to earth. Einstein's general relativity predicts that the sun will cause the surrounding space and time to warp and such distortion will influence the path taken by the starlight. After all, the photons of distant origin travel along the fabric of the universe; if the fabric is warped, the motion of the photons will be affected much as for a material body. The bending of the path of light is greatest for those light signals that just graze the sun on their way to earth. A solar eclipse makes it possible to see such sun-grazing starlight without its being completely obscured by sunlight itself.
The angle through which the light path is bent can be measured in a simple way. The bending of the starlight's path results in a shift in the apparent position of the star. The shift can be accurately measured by comparing this apparent position with the star's actual location known from observations of the star at night (in the absence of the sun's warping influence), carried out when the earth is at an appropriate position, some six months earlier or later. In November of 1915, Einstein used his new understanding of gravity to calculate the angle through which starlight signals that just graze the sun would be bent and found the answer to be about.00049 of a degree (1.75 arcseconds, where an arcsecond is 1/3600 of a degree). This tiny angle is equal to that subtended by a quarter placed upright and viewed from nearly two miles away. The detection of such a small angle was, however, within reach of the technology of the day. At the urging of Sir Frank Dyson, director of the Greenwich observatory, Sir Arthur Eddington, a well-known astronomer and secretary of the Royal Astronomical Society in England, organized an expedition to the island of Principe off the coast of West Africa to test Einstein's prediction during the solar eclipse of May 29, 1919.
On November 6, 1919, after some five months of analysis of the photographs taken during the eclipse at Principe (and of other photographs of the eclipse taken by a second British team led by Charles Davidson and Andrew Crommelin in Sobral, Brazil), it was announced at a joint meeting of the Royal Society and the Royal Astronomical Society that Einstein's prediction based on general relativity had been confirmed. It took little time for word of this success—a complete overturning of previous conceptions of space and time—to spread well beyond the confines of the physics community, making Einstein a celebrated figure worldwide. On November 7, 1919, the headline in the London Times read "REVOLUTION IN SCIENCE—NEW THEORY OF THE UNIVERSE—NEWTONIAN IDEAS OVERTHROWN."11This was Einstein's moment of glory.
In the years following this experiment, Eddington's confirmation of general relativity came under some critical scrutiny. Numerous difficult and subtle aspects of the measurement made it hard to reproduce and raised some questions regarding the trustworthiness of the original experiment. Nevertheless, in the last 40 years a variety of experiments making use of technological advancements have tested numerous aspects of general relativity with great precision. The predictions of general relativity have been uniformly confirmed. There is no longer any doubt that Einstein's description of gravity is not only compatible with special relativity, but yields predictions closer to experimental results than those of Newton's theory.
Black Holes, the Big Bang, and the Expansion of Space
Whereas special relativity is most manifest when things are moving fast, general relativity comes into its own when things are very massive and the warps in space and time are correspondingly severe. Let's describe two examples.
The first is a discovery made by the German astronomer Karl Schwarzschild while studying Einstein's revelations on gravity in between his own calculations of artillery trajectories at the Russian front during World War I in 1916. Remarkably, just months after Einstein had put the finishing touches on general relativity, Schwarzschild was able to use the theory to gain a complete and exact understanding of the way space and time warp in the vicinity of a perfectly spherical star. Schwarzschild sent his results from the Russian front to Einstein, who presented them on Schwarzschild's behalf to the Prussian Academy.
Beyond confirming and making mathematically precise the warping that was schematically illustrated in Figure 3.5, Schwarzschild's work—which has now come to be known as "Schwarzschild's solution"—revealed a stunning implication of general relativity. He showed that if the mass of a star is concentrated in a small enough spherical region, so that its mass divided by its radius exceeds a particular critical value, the resulting spacetime warp is so radical that anything, including light, that gets too close to the star will be unable to escape its gravitational grip. Since not even light can escape such "compressed stars," they were initially called dark or frozen stars. A more catchy name was coined years later by John Wheeler, who called them black holes—black because they cannot emit light, holes because anything getting too close falls into them, never to return. The name stuck.
We illustrate Schwarzschild's solution in Figure 3.7. Although black holes have a reputation for rapacity, objects that pass by them at a "safe" distance are deflected in much the same way that they would be by an ordinary star, and can proceed on their merry way. But objects of any composition whatsoever that get too close—closer than what has been termed the black hole's event horizon—are doomed: they will be drawn inexorably toward the center of the black hole and subject to an ever increasing and ultimately destructive gravitational strain. For example, if you dropped feet first through the event horizon, as you approached the black hole's center you would find yourself getting increasingly uncomfortable. The gravitational force of the black hole would increase so dramatically that its pull on your feet would be much stronger than its pull on your head (since in a feet-first fall your feet are always a bit closer than your head to the black hole's center); so much stronger, in fact, that you would be stretched with a force that would quickly tear your body to shreds.
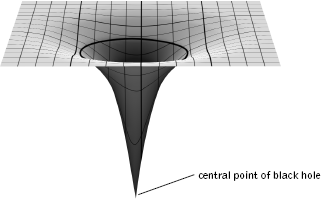
Figure 3.7 A black hole warps the surrounding spacetime fabric so severely that anything that comes within its "event horizon"—illustrated by the dark circle—can't escape from its gravitational grip. No one knows exactly what happens at the deepest interior point of a black hole.
If, on the contrary, you were more prudent in your wanderings near a black hole and took great care not to trespass beyond the event horizon, you could make use of the black hole for a rather amazing feat. Imagine, for example, that you were to discover a black hole whose mass was about 1,000 times the mass of the sun, and that you were to lower yourself on a cable, much as George did near the sun, to about an inch above the black hole's event horizon. As we have discussed, gravitational fields cause a warping of time, and this means that your passage through time would slow down. In fact, since black holes have such strong gravitational fields, your passage through time would slow way down. Your watch would tick about ten thousand times more slowly than those of your friends back on earth. If you were to hover just above the black hole's event horizon in this manner for a year, and then climb up the cable to your waiting starship for a short, yet leisurely, journey home, upon arrival at earth you would find that more than ten thousand years had passed since your initial departure. You would have successfully used the black hole as a kind of time machine, allowing you to travel to earth's distant future.
To get a sense of the extreme scales involved, a star with the mass of the sun would be a black hole if its radius were not its actual value (about 450,000 miles), but, instead, just under 2 miles. Imagine: The whole of the sun squeezed to fit comfortably within upper Manhattan. A teaspoonful of such a compressed sun would weigh about as much as Mount Everest. To make a black hole out of the earth we would need to crush it into a sphere whose radius is less than half an inch. For a long time physicists were skeptical about whether such extreme configurations of matter could ever actually occur, and many thought that black holes were merely a reflection of an overworked theoretician's imagination.
Nevertheless, during the last decade, an increasingly convincing body of experimental evidence for the existence of black holes has accumulated. Of course, since they are black, they cannot be observed directly by scanning the sky with telescopes. Instead, astronomers search for black holes by seeking anomalous behavior of other more ordinary light-emitting stars that may be positioned just outside a black hole's event horizon. For instance, as dust and gas from the outer layers of nearby ordinary stars fall toward the event horizon of a black hole, they are accelerated to nearly the speed of light. At such speeds, friction within the maelstrom of downward-swirling material generates an enormous amount of heat, causing the dust-gas mixture to "glow," giving off both ordinary visible light and X rays. Since this radiation is produced just outside the event horizon, it can escape the black hole and travel through space to be observed and studied directly. General relativity makes detailed predictions about properties that such X ray emissions will have; observation of these predicted properties gives strong, albeit indirect, evidence for the existence of black holes. For example, mounting evidence indicates that there is a very massive black hole, some two and a half million times as massive as the sun, sitting in the center of our own Milky Way galaxy. And even this seemingly gargantuan black hole pales in comparison to what astronomers believe to reside in the core of the astonishingly luminous quasars that are scattered throughout the cosmos: black holes whose masses may well be billions of times that of the sun.
Schwarzschild died only a few months after finding his solution, from a skin disease he contracted at the Russian front. He was 42. His tragically brief encounter with Einstein's theory of gravity uncovered one of the most striking and mysterious facets of the natural world.
The second example in which general relativity flexes its muscle concerns the origin and evolution of the whole universe. As we have seen, Einstein showed that space and time respond to the presence of mass and energy. This distortion of spacetime affects the motion of other cosmic bodies moving in the vicinity of the resulting warps. In turn, the precise way in which these bodies move, by virtue of their own mass and energy, has a further effect on the warping of spacetime, which further affects the motion of the bodies, and on and on the interconnected cosmic dance goes. Through the equations of general relativity, equations rooted in geometrical insights into curved space spearheaded by the great nineteenth-century mathematician Georg Bernhard Riemann (more about Riemann later), Einstein was able to describe the mutual evolution of space, time, and matter quantitatively. To his great surprise, when the equations are applied beyond an isolated context within the universe, such as a planet or a comet orbiting a star, to the universe as a whole, a remarkable conclusion is reached: the overall size of the spatial universe must be changing in time. That is, either the fabric of the universe is stretching or it is shrinking, but it is not simply staying put. The equations of general relativity show this explicitly.
This conclusion was too much even for Einstein. He had overturned the collective intuition regarding the nature of space and time built up through everyday experiences over thousands of years, but the notion of an always existing, never changing universe was too ingrained for even this radical thinker to abandon. For this reason, Einstein revisited his equations and modified them by introducing something known as a cosmological constant, an additional term that allowed him to avoid this prediction and once again bask in the comfort of a static universe. However, 12 years later, through detailed measurements of distant galaxies, the American astronomer Edwin Hubble experimentally established that the universe is expanding. In a now-famous story in the annals of science, Einstein then returned to the original form of his equations, citing his temporary modification of them as the biggest blunder of his life.12 His initial unwillingness to accept the conclusion notwithstanding, Einstein's theory predicted the expansion of the universe. In fact, in the early 1920s—years before Hubble's measurements—the Russian meteorologist Alexander Friedmann had used Einstein's original equations to show, in some detail, that all galaxies would be carried along on the substrate of stretching spatial fabric, thereby speedily moving away from all others. Hubble's observations and numerous subsequent ones have thoroughly verified this astonishing conclusion of general relativity. By offering the explanation for the expansion of the universe, Einstein achieved one of the greatest intellectual feats of all time.
If the fabric of space is stretching, thereby increasing the distance between galaxies that are carried along on the cosmic flow, we can imagine running the evolution backward in time to learn about the origin of the universe. In reverse, the fabric of space shrinks, bringing all galaxies closer and closer to each other. Like the contents of a pressure cooker, as the shrinking universe compresses the galaxies together, the temperature dramatically increases, stars disintegrate and a hot plasma of matter's elementary constituents is formed. As the fabric continues to shrink, the temperature rises unabated, as does the density of the primordial plasma. As we imagine running the clock backward from the age of the presently observed universe, about 15 billion years, the universe as we know it is crushed to an ever smaller size. The matter making up everything—every car, house, building, mountain on earth; the earth itself; the moon; Saturn, Jupiter, and every other planet; the sun and every other star in the Milky Way; the Andromeda galaxy with its 100 billion stars and each and every other of the more than 100 billion galaxies—is squeezed by a cosmic vise to astounding density. And as the clock is turned back to ever earlier times, the whole of the cosmos is compressed to the size of an orange, a lemon, a pea, a grain of sand, and to yet tinier size still. Extrapolating all the way back to "the beginning," the universe would appear to have begun as a point—an image we will critically re-examine in later chapters—in which all matter and energy is squeezed together to unimaginable density and temperature. It is believed that a cosmic fireball, the big bang, erupted from this volatile mixture spewing forth the seeds from which the universe as we know it evolved.
The image of the big bang as a cosmic explosion ejecting the material contents of the universe like shrapnel from an exploding bomb is a useful one to bear in mind, but it is a little misleading. When a bomb explodes, it does so at a particular location in space and at a particular moment in time. Its contents are ejected into the surrounding space. In the big bang, there is no surrounding space. As we devolve the universe backward toward the beginning, the squeezing together of all material content occurs because all of space is shrinking. The orange-size, the pea-size, the grain of sand-size devolution describes the wholeof the universe—not something within the universe. Carrying on to the beginning, there is simply no space outside the primordial pinpoint grenade. Instead, the big bang is the eruption of compressed space whose unfurling, like a tidal wave, carries along matter and energy even to this day.
Is General Relativity Right?
No deviations from the predictions of general relativity have been found in experiments performed with our present level of technology. Only time will tell if greater experimental precision will ultimately uncover some, thereby showing this theory, too, to be only an approximate description of how nature actually works. The systematic testing of theories to greater and greater levels of accuracy is, certainly, one of the ways science progresses, but it is not the only way. In fact, we have already seen this: The search for a new theory of gravity was initiated, not by an experimental refutation of Newton's theory, but rather by the conflict of Newtonian gravity with another theory—special relativity. It was only after the discovery of general relativity as a competing theory of gravity that experimental flaws in Newton's theory were identified by seeking out tiny but measurable ways in which the two theories differ. Thus, internal theoretical inconsistencies can play as pivotal a role in driving progress as do experimental data.
For the last half century, physics has been faced with still another theoretical conflict whose severity is on par with that between special relativity and Newtonian gravity. General relativity appears to be fundamentally incompatible with another extremely well-tested theory: quantum mechanics. Regarding the material covered in this chapter, the conflict prevents physicists from understanding what really happens to space, time, and matter when crushed together fully at the moment of the big bang or at the central point of a black hole. But more generally, the conflict alerts us to a fundamental deficiency in our conception of nature. The resolution of this conflict has eluded attempts by some of the greatest theoretical physicists, giving it a well-deserved reputation as the central problem of modern theoretical physics. Understanding the conflict requires familiarity with some basic features of quantum theory, to which we now turn.