The Elegant Universe: Superstrings, Hidden Dimensions, and the Quest for the Ultimate Theory - Brian Greene (2010)
Part IV. String Theory and the Fabric of Spacetime
Chapter 14. Reflections on Cosmology
Humans throughout history have had a passionate drive to understand the origin of the universe. There is, perhaps, no single question that so transcends cultural and temporal divides, inspiring the imagination of our ancient forebears as well as the research of the modern cosmologist. At a deep level, there is a collective longing for an explanation of why there is a universe, how it has come to take the form we witness, and for the rationale—the principle—that drives its evolution. The astounding thing is that humanity has now come to a point where a framework is emerging for answering some of these questions scientifically.
The currently accepted scientific theory of creation declares that the universe experienced the most extreme of conditions—enormous energy, temperature, and density—during its earliest moments. These conditions, as is by now familiar, require that both quantum mechanics and gravity be taken into account, and hence the birth of the universe provides a profound arena for exercising the insights of superstring theory. We will discuss these nascent insights shortly, but first, we briefly recount the pre-string theory cosmological story, which is often referred to as the standard model of cosmology.
The Standard Model of Cosmology
The modern theory of cosmic origins dates from the decade and a half after Einstein's completion of general relativity. Although Einstein refused to take his own theory at face value and accept that it implies that the universe is neither eternal nor static, Alexander Friedmann did. And as we discussed in Chapter 3, Friedmann found what is now known as the big bang solution to Einstein's equations—a solution that declares that the universe violently emerged from a state of infinite compression, and is currently in the expanding aftermath of that primeval explosion. So certain was Einstein that such time-varying solutions were not a result of his theory that he published a short article claiming to have found a fatal flaw in Friedmann's work. Some eight months later, however, Friedmann succeeded in convincing Einstein that there was, in fact, no flaw; Einstein publicly but curtly retracted his objection. Nevertheless, it is clear that Einstein did not think Friedmann's results had any relevance to the universe. But about five years later, Hubble's detailed observations of a few dozen galaxies with the hundred-inch telescope at Mount Wilson Observatory confirmed that, indeed, the universe is expanding. Friedmann's work, refashioned in a more systematic and efficient form by the physicists Howard Robertson and Arthur Walker, still forms the foundation of modern cosmology.
In a little more detail, the modern theory of cosmic origins goes like this. Some 15 billion or so years ago, the universe erupted from an enormously energetic, singular event, which spewed forth all of space and all of matter. (You don't have to search far to locate where the big bang occurred, for it took place where you are now as well as everywhere else; in the beginning, all locations we now see as separate were the same location.) The temperature of the universe a mere 10-43 seconds after the bang, the so-called Planck time, is calculated to have been about 1032 Kelvin, some 10 trillion trillion times hotter than the deep interior of the sun. As time passed, the universe expanded and cooled, and as it did, the initial homogeneous, roiling hot, primordial cosmic plasma began to form eddies and clumps. At about a hundred-thousandth of a second after the bang, things had cooled sufficiently (to about 10 trillion Kelvin—about a million times hotter than the sun's interior) for quarks to clump together in groups of three, forming protons and neutrons. About a hundredth of a second later, conditions were right for the nuclei of some of the lightest elements in the periodic table to start congealing out of the cooling plasma of particles. For the next three minutes, as the simmering universe cooled to about a billion degrees, the predominant nuclei that emerged were those of hydrogen and helium, along with trace amounts of deuterium ("heavy" hydrogen) and lithium. This is known as the period of primordial nucleosynthesis.
Not a whole lot happened for the next few hundred thousand years, other than further expansion and cooling. But then, when the temperature had dropped to a few thousand degrees, wildly streaming electrons slowed down to the point where atomic nuclei, mostly hydrogen and helium, could capture them, forming the first electrically neutral atoms. This was a pivotal moment: from this point forward the universe, by and large, became transparent. Prior to the era of electron capture, the universe was filled with a dense plasma of electrically charged particles—some with positive charges like nuclei and others with negative charges, like electrons. Photons, which interact only with electrically charged objects, were bumped and jostled incessantly by the thick bath of charged particles, traversing hardly any distance before being deflected or absorbed. The charged-particle barrier to the free motion of photons would have made the universe appear almost completely opaque, much like what you may have experienced in a dense morning fog or a blinding, gusty snowstorm. But when negatively charged electrons were brought into orbit around positively charged nuclei, yielding electrically neutral atoms, the charged obstructions disappeared and the dense fog lifted. From that time onward, photons from the big bang have traveled unhindered and the full expanse of the universe gradually came into view.
About a billion years later, with the universe having substantially calmed down from its frenetic beginnings, galaxies, stars, and ultimately planets began to emerge as gravitationally bound clumps of the primordial elements. Today, some 15 billion or so years after the bang, we can marvel at both the magnificence of the cosmos and at our collective ability to have pieced together a reasonable and experimentally testable theory of cosmic origin.
But how much faith should we really have in the big bang theory?
Putting the Big Bang to the Test
By looking out into the universe with their most powerful telescopes, astronomers can see light that was emitted from galaxies and quasars just a few billion years after the big bang. This allows them to verify the expansion of the universe predicted by the big bang theory back to this early phase of the universe, and everything checks out to a "T." To test the theory to yet earlier times, physicists and astronomers must make use of more indirect methods. One of the most refined approaches involves something known as cosmic background radiation.
If you've ever felt a bicycle tire after vigorously pumping it full of air, you know that it is warm to the touch. Some of the energy you expend in the repeated pumping motion is transferred to an increase in temperature of the air in the tire. This reflects a general principle: Under a wide variety of conditions, when things are compressed they heat up. Reasoning in reverse, when things are allowed to decompress—to expand—they cool down. Air conditioners and refrigerators rely on these principles, subjecting substances like freon to repeated cycles of compression and expansion (as well as evaporation and condensation) to cause heat flow in the desired direction. Although these are simple facts of terrestrial physics, it turns out that they have a profound incarnation in the cosmos as a whole.
We saw above that after electrons and nuclei join together to form atoms, photons are free to travel unimpeded throughout the universe. This means that the universe is filled with a "gas" of photons traveling this way and that, uniformly distributed throughout the cosmos. As the universe expands, this gas of freely streaming photons expands as well since, in essence, the universe is its container. And just as the temperature of a more conventional gas (like the air in a bicycle tire) decreases as it expands, the temperature of this photon gas decreases as the universe expands. In fact, physicists as far back as George Gamow and his students Ralph Alpher and Robert Hermann in the 1950s, and Robert Dicke and Jim Peebles in the mid-1960s, realized that the present-day universe should be permeated by an almost uniform bath of these primordial photons, which, through the last 15 billion years of cosmic expansion, have cooled to a mere handful of degrees above absolute zero.1 In 1965, Arno Penzias and Robert Wilson of Bell Laboratories in New Jersey accidentally made one of the most important discoveries of our age when they detected this afterglow of the big bang while working on an antenna intended for use with communication satellites. Subsequent research has refined both theory and experiment, culminating in measurements taken by NASA's COBE (Cosmic Background Explorer) satellite in the early 1990s. With these data, physicists and astronomers have confirmed to high precision that the universe is filled with microwave radiation (if our eyes were sensitive to microwaves, we would see a diffuse glow in the world around us) whose temperature is about 2.7 degrees above absolute zero, exactly in keeping with the expectation of the big bang theory. In concrete terms, in every cubic meter of the universe—including the one you now occupy—there are, on average, about 400 million photons that collectively compose the vast cosmic sea of microwave radiation, an echo of creation. A percentage of the "snow" you see on your television screen when you disconnect the cable feed and tune to a station that has ceased its scheduled broadcasts is due to this dim aftermath of the big bang. This match between theory and experiment confirms the big bang picture of cosmology as far back as the time that photons first moved freely through the universe, about a few hundred thousand years after the bang (ATB).
Can we push further in our tests of the big bang theory to even earlier times? We can. By using standard principles of nuclear theory and thermodynamics, physicists can make definite predictions about the relative abundance of the light elements produced during the period of primordial nucleosynthesis, between a hundredth of a second and a few minutes ATB. According to theory, for example, about 23 percent of the universe should be composed of helium. By measuring the helium abundance in stars and nebulae, astronomers have amassed impressive support that, indeed, this prediction is right on the mark. Perhaps even more impressive is the prediction and confirmation regarding deuterium abundance, since there is essentially no astrophysical process, other than the big bang, that can account for its small but definite presence throughout the cosmos. The confirmation of these abundances, and more recently that of lithium, is a sensitive test of our understanding of early universe physics back to the time of their primordial synthesis.
This is impressive almost to the point of hubris. All the data we possess confirm a theory of cosmology capable of describing the universe from about a hundredth of a second ATB to the present, some 15 billion years later. Nevertheless, one should not lose sight of the fact that the newborn universe evolved with phenomenal haste. Tiny fractions of a second—fractions much smaller than a hundredth of a second—form cosmic epochs during which long-lasting features of the world were first imprinted. And so, physicists have continued to push onward, trying to explain the universe at ever earlier times. Since the universe gets ever smaller, hotter, and denser as we push back, an accurate quantum-mechanical description of matter and the forces becomes increasingly important. As we have seen from other viewpoints in earlier chapters, point-particle quantum field theory works until typical particle energies are around the Planck energy. In a cosmological context, this occurred when the whole of the known universe fit within a Planck-sized nugget, yielding a density so great that it strains one's ability to find a fitting metaphor or an enlightening analogy: the density of the universe at the Planck time was simply colossal. At such energies and densities gravity and quantum mechanics can no longer be treated as two separate entities as they are in point-particle quantum field theory. Instead, the central message of this book is that at and beyond these enormous energies we must invoke string theory. In temporal terms, we encounter these energies and densities when we probe earlier than the Planck time of 10-43 seconds ATB, and hence this earliest epoch is the cosmological arena of string theory.
Let's head toward this era by first seeing what the standard cosmological theory tells us about the universe before a hundredth of a second ATB, but after the Planck time.
From the Planck Time to a Hundredth of a Second ATB
Recall from Chapter 7 (especially Figure 7.1) that the three nongravitational forces appear to merge together in the intensely hot environment of the early universe. Physicists' calculations of how the strengths of these forces vary with energy and temperature show that prior to about 10-35 seconds ATB, the strong, weak, and electromagnetic forces were all one "grand unified" or "super" force. In this state the universe was far more symmetric than it is today. Like the homogeneity that follows when a collection of disparate metals is heated to a smooth molten liquid, the significant differences between the forces as we now observe them were all erased by the extremes of energy and temperature encountered in the very early universe. But as time went by and the universe expanded and cooled, the formalism of quantum field theory shows that this symmetry would have been sharply reduced through a number of rather abrupt steps, ultimately leading to the comparatively asymmetric form with which we are familiar.
It's not hard to understand the physics behind such reduction of symmetry, or symmetry breaking, as it is more precisely called. Picture a large container filled with water. The molecules of H2O are uniformly spread throughout the container and regardless of the angle from which you view it, the water looks the same. Now watch the container as you lower the temperature. At first not much happens. On microscopic scales, the average speed of the water molecules decreases, but that's about all. When you decrease the temperature to 0 degrees Celsius, however, you suddenly see that something drastic occurs. The liquid water begins to freeze and turn into solid ice. As discussed in the preceding chapter, this is a simple example of a phase transition. For our present purpose, the important thing to note is that the phase transition results in a decrease in the amount of symmetry displayed by the H2O molecules. Whereas liquid water looks the same regardless of the angle from which it is viewed—it appears to be rotationally symmetric—solid ice is different. It has a crystalline block structure, which means that if you examine it with adequate precision, it will, like any crystal, look different from different angles. The phase transition has resulted in a decrease in the amount of rotational symmetry that is manifest.
Although we have discussed only one familiar example, the point is true more generally: as we lower the temperature of many physical systems, at some point they undergo a phase transition that typically results in a decrease or a "breaking" of some of their previous symmetries. In fact, a system can go through a series of phase transitions if its temperature is varied over a wide enough range. Water, again, provides a simple example. If we start with H2O above 100 degrees Celsius, it is a gas: steam. In this form, the system has even more symmetry than in the liquid phase since now the individual H2O molecules have been liberated from their congested, stuck-together liquid form. Instead, they all zip around the container on completely equal footing, without forming any clumps or "cliques" in which groups of molecules single each other out for a close association at the expense of others. Molecular democracy prevails at high enough temperatures. As we lower the temperature below 100 degrees, of course, water droplets do form as we pass through a gas-liquid phase transition, and the symmetry is reduced. Continuing on to yet lower temperatures, nothing too dramatic happens until we pass through 0 degrees Celsius, when, as above, the liquid-water/solid-ice phase transition results in another abrupt decrease in symmetry.
Physicists believe that between the Planck time and a hundredth of a second ATB, the universe behaved in a very similar way, passing through at least two analogous phase transitions. At temperatures above 1028 Kelvin, the three nongravitational forces appeared as one, as symmetric as they could possibly be. (At the end of this chapter we will discuss string theory's inclusion of the gravitational force into this high-temperature merger.) But as the temperature dropped below 1028 Kelvin, the universe underwent a phase transition in which the three forces crystallized out from their common union in different ways. Their relative strengths and the details of how they act on matter began to diverge. And so, the symmetry among the forces evident at higher temperatures was broken as the universe cooled. Nevertheless, the work of Glashow, Salam, and Weinberg (see Chapter 5) shows that not all of the high-temperature symmetry was erased: The weak and electromagnetic forces were still deeply interwoven. As the universe further expanded and cooled, nothing much happened until things simmered down to 1015 Kelvin—about 100 million times the sun's core temperature—when the universe went through another phase transition that affected the electromagnetic and weak forces. At this temperature, they too crystallized out from their previous, more symmetric union, and as the universe continued to cool, their differences became magnified. The two phase transitions are responsible for the three apparently distinct nongravitational forces at work in the world, even though this review of cosmic history shows that the forces, in fact, are deeply related.
A Cosmological Puzzle
This post-Planck era cosmology provides an elegant, consistent, and calculationally tractable framework for understanding the universe as far back as the briefest moments after the bang. But, as with most successful theories, our new insights raise yet more detailed questions. And it turns out that some of these questions, while not invalidating the standard cosmological scenario as presented, do highlight awkward aspects that point toward the need for a deeper theory. Let's focus on one. It is called the horizon problem, and it is one of the most important issues in modern cosmology.
Detailed studies of the cosmic background radiation have shown that regardless of which direction in the sky one points the measuring antenna, the temperature of the radiation is the same, to about one part in 100,000. If you think about it for a moment, you will realize that this is quite strange. Why should different locations in the universe, separated by enormous distances, have temperatures that are so finely matched? A seemingly natural resolution to this puzzle is to note that, yes, two diametrically opposite places in the heavens are far apart today, but like twins separated at birth, during the earliest moments of the universe they (and everything else) were very close together. Since they emerged from a common starting point, you might suggest that it's not at all surprising that they share common physical traits such as their temperature.
In the standard big bang cosmology this suggestion fails. Here's why. A bowl of hot soup gradually cools to room temperature because it is in contact with the colder surrounding air. If you wait long enough, the temperature of the soup and the air will, through their mutual contact, become the same. But if the soup is in a thermos, of course, it retains its heat for much longer, since there is far less communication with the outside environment. This reflects that the homogenization of temperature between two bodies relies on their having prolonged and unimpaired communication. To test the suggestion that positions in space that are currently separated by vast distances share the same temperature because of their initial contact, we must therefore examine the efficacy of information exchange between them in the early universe. At first you might think that since the positions were closer together at earlier times, communication was ever easier. But spatial proximity is only one part of the story. The other part is temporal duration.
To examine this more fully, let's imagine studying a "film" of the cosmic expansion, but let's review it in reverse, running the film backward in time from today toward the moment of the big bang. Since the speed of light sets a limit to how fast any signal or information of any kind can travel, matter in two regions of space can exchange heat energy and thereby have a chance of coming to a common temperature only if the distance between them at a given moment is less than the distance light can have traveled since the time of the big bang. And so, as we roll the film backward in time we see that there is a competition between how close together our spatial regions become versus how far back we have to turn the clock for them to get there. For instance, if in order for the separation of our two spatial locations to be 186,000 miles, we have to run the film back to less than a second ATB, then even though they are much closer, there is still no way for them to have any influence on each other since light would require a whole second to travel the distance between them.2 If in order for their separation to be much less, say 186 miles, we have to run the film back to less than a thousandth of a second ATB, then, again, the same conclusion follows: They can't influence each other since in less than a thousandth of a second light can't travel the 186 miles separating them. Carrying on in the same vein, if we have to run the film back to less than a billionth of a second ATB in order for these regions to be within one foot of each other, they still cannot influence each other since there is just not enough time since the bang for light to have traveled the 12 inches between them. This shows that just because two points in the universe get closer and closer as we head back to the bang, it is not necessarily the case that they can have had the thermal contact—like that between soup and air—necessary to bring them to the same temperature.
Physicists have shown that precisely this problem arises in the standard big bang model. Detailed calculations show that there is no way for regions of space that are currently widely separated to have had the exchange of heat energy that would explain their having the same temperature. As the word horizon refers to how far we can see—how far light can travel, so to speak—physicists call the unexplained uniformity of temperature throughout the vast expanse of the cosmos the "horizon problem." The puzzle does not mean the standard cosmological theory is wrong. But the uniformity of temperature does strongly suggest that we are missing an important part of the cosmological story. In 1979, the physicist Alan Guth, now of the Massachusetts Institute of Technology, wrote the missing chapter.
Inflation
The root of the horizon problem is that in order to get two widely separated regions of the universe close together, we have to run the cosmic film way back toward the beginning of time. So far back, in fact, that there is not enough time for any physical influence to have traveled from one region to the other. The difficulty, therefore, is that as we run the cosmological film backward and approach the big bang, the universe does not shrink at a fast enough rate.
Well, that's the rough idea, but it's worthwhile sharpening the description a bit. The horizon problem stems from the fact that like a ball tossed upward, the dragging pull of gravity causes the expansion rate of the universe to slow down. This means that, for example, to halve the separation between two locations in the cosmos we must run the film back more than halfway toward its beginning. In turn, we see that to halve the separation we must more than halve the time since the big bang. Less time since the bang—proportionally speaking—means it is harder for the two regions to communicate, even though they get closer.
Guth's resolution of the horizon problem is now simple to state. He found another solution to Einstein's equations in which the very early universe undergoes a brief period of enormously fast expansion—a period during which it "inflates" in size at an unheralded exponential expansion rate. Unlike the case of a ball that slows down after being tossed upward, exponential expansion gets faster as it proceeds. When we run the cosmic film in reverse, rapid accelerating expansion turns into rapid decelerating contraction. This means that to halve the separation between two locations in the cosmos (during the exponential epoch) we need run the the film back less than halfway—much less, in fact. Running the film back less implies that the two regions will have had more time to communicate thermally and, like hot soup and air, they will have had ample time to come to the same temperature.
Through Guth's discovery and later important refinements made by Andrei Linde, now of Stanford University, Paul Steinhardt and Andreas Albrecht, then of the University of Pennsylvania, and many others, the standard cosmological model was revamped into the inflationary cosmological model. In this framework, the standard cosmological model is modified during a tiny window of time—around 10-36 to 10-34 seconds ATB—in which the universe expanded by a colossal factor of at least 1030, compared with a factor of about a hundred during the same time interval in the standard scenario. This means that in a brief flicker of time, about a trillionth of a trillionth of a trillionth of a second ATB, the size of the universe increased by a greater percentage than it has in the 15 billion years since. Before this expansion, matter that is now in far-flung regions of the cosmos was much closer together than in the standard cosmological model, making it possible for a common temperature to be easily established. Then, through Guth's momentary burst of cosmological inflation—followed by the more usual expansion of the standard cosmological model—these regions of space were able to become separated by the vast distances we witness currently. And so, the brief but profound inflationary modification of the standard cosmological model solves the horizon problem (as well as a number of other important problems we have not discussed) and has gained wide acceptance among cosmologists.3
We summarize the history of the universe from just after the Planck time to the present, according to the current theory, in Figure 14.1.
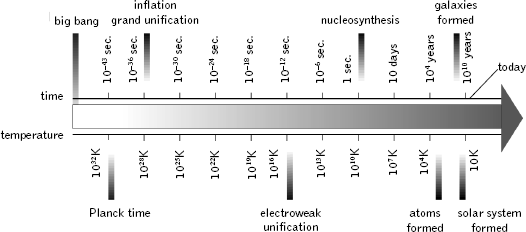
Figure 14.1 A time line denoting a few key moments in the history of the universe.
Cosmology and Superstring Theory
There remains a sliver of Figure 14.1, between the big bang and the Planck time, that we have not yet discussed. By blindly applying the equations of general relativity to that region, physicists have found that the universe continues to get ever smaller, ever hotter, and ever denser, as we move backward in time toward the bang. At time zero, as the size of the universe vanishes, the temperature and density soar to infinity, giving us the most extreme signal that this theoretical model of the universe, firmly rooted in the classical gravitational framework of general relativity, has completely broken down.
Nature is telling us emphatically that under such conditions we must merge general relativity and quantum mechanics—in other words, we must make use of string theory. Currently, research on the implications of string theory for cosmology is at an early stage of development. Perturbative methods can, at best, give skeletal insights, since the extremes of energy, temperature, and density require precision analysis. Although the second superstring revolution has provided some nonperturbative techniques, it will be some time before they are honed for the kinds of calculations required in a cosmological setting. Nevertheless, as we now discuss, during the last decade or so, physicists have taken the first steps toward understanding string cosmology. Here is what they have found.
It appears that there are three essential ways in which string theory modifies the standard cosmological model. First, in a manner that current research continues to clarify, string theory implies that the universe has what amounts to a smallest possible size. This has profound consequences for our understanding of the universe at the moment of the bang itself, when the standard theory claims that its size has shrunk all the way to zero. Second, string theory has a small-radius/large-radius duality (intimately related to its having a smallest possible size), which also has deep cosmological significance, as we will see in a moment. Finally, string theory has more than four spacetime dimensions, and from a cosmological standpoint, we must address the evolution of them all. Let's discuss these points in greater detail.
In the Beginning There Was a Planck-Sized Nugget
In the late 1980s, Robert Brandenberger and Cumrun Vafa made the first important strides toward understanding how the application of these string theoretic features modifies the conclusions of the standard cosmological framework. They came to two important realizations. First, as we run the clock backward in time toward the beginning, the temperature continues to rise until the size of the universe is about the Planck length in all directions. But then, the temperature hits a maximum and begins to decrease. The intuitive reason behind this is not hard to come by. Imagine for simplicity (as Brandenberger and Vafa did) that all of the space dimensions of the universe are circular. As we run the clock backward and the radius of each of these circles shrinks, the temperature of the universe increases. But as each of the radii collapses toward and then through the Planck length, we know that, within string theory, this is physically identical to the radii shrinking to the Planck length and then bouncing back toward increasing size. Since temperature goes down as the universe expands, we would expect that the futile attempt to squeeze the universe to sub-Planck size means that the temperature stops rising, hits a maximum, and then begins to decrease. Through detailed calculations, Brandenberger and Vafa explicitly verified that indeed this is the case.
This led Brandenberger and Vafa to the following cosmological picture. In the beginning, all of the spatial dimensions of string theory are tightly curled up to their smallest possible extent, which is roughly the Planck length. The temperature and energy are high, but not infinite, since string theory has avoided the conundrums of an infinitely compressed zero-size starting point. At this beginning moment of the universe, all the spatial dimensions of string theory are on completely equal footing—they are completely symmetric—all curled up into a multidimensional, Planck-sized nugget. Then, according to Brandenberger and Vafa, the universe goes through its first stage of symmetry reduction when, at about the Planck time, three of the spatial dimensions are singled out for expansion, while all others retain their initial Planck-scale size. These three space dimensions are then identified with those in the inflationary cosmological scenario, the post-Planck-time evolution summarized in Figure 14.1 takes over, and these three dimensions expand to their currently observed form.
Why Three?
An immediate question is, What drives the symmetry reduction that singles out precisely three spatial dimensions for expansion? That is, beyond the experimental fact that only three of the space dimensions have expanded to observably large size, does string theory provide a fundamental reason for why some other number (four, five, six, and so on) or, even more symmetrically, all of the space dimensions don't expand as well? Brandenberger and Vafa came up with a possible explanation. Remember that the small-radius/large-radius duality of string theory rests upon the fact that when a dimension is curled up like a circle, a string can wrap around it. Brandenberger and Vafa realized that, like rubber bands wrapped around a bicycle tire inner tube, such wrapped strings tend to constrict the dimensions they encircle, keeping them from expanding. At first sight, this would seem to mean that each of the dimensions will be constricted, since the strings can and do wrap them all. The loophole is that if a wrapped string and its antistring partner (roughly, a string that wraps the dimension in the opposite direction) should come into contact, they will swiftly annihilate one other, producing an unwrapped string. If these processes happen with sufficient rapidity and efficiency, enough of the rubber band-like constriction will be eliminated, allowing the dimensions to expand. Brandenberger and Vafa suggested that this reduction in the choking effect of wrapped strings will happen in only three of the spatial dimensions. Here's why.
Imagine two point particles rolling along a one-dimensional line such as the spatial extent of Lineland. Unless they happen to have identical velocities, sooner or later one will overtake the other, and they will collide. Notice, however, that if these same point particles are randomly rolling around on a two-dimensional plane such as the spatial extent of Flatland, it is likely that they will never collide. The second spatial dimension opens up a new world of trajectories for each particle, most of which do not cross each other at the same point at the same time. In three, four, or any higher number of dimensions, it gets increasingly unlikely that the two particles will ever meet. Brandenberger and Vafa realized that an analogous idea holds if we replace point particles with loops of string, wrapped around spatial dimensions. Although it's significantly harder to see, if there are three (or fewer) circular spatial dimensions, two wrapped strings will likely collide with one another—the analog of what happens for two particles moving in one dimension. But in four or more space dimensions, wrapped strings are less and less likely ever to collide—the analog of what happens for point particles in two or more dimensions.4
This leads to the following picture. In the first moment of the universe, the tumult from the high, but finite, temperature drives all of the circular dimensions to try to expand. As they do, the wrapped strings constrict the expansion, driving the dimensions back to their original Planck-size radii. But, sooner or later a random thermal fluctuation will drive three dimensions momentarily to grow larger than the others, and our discussion then shows that strings which wrap these dimensions are highly likely to collide. About half of the collisions will involve string/antistring pairs, leading to annihilations that continually lessen the constriction, allowing these three dimensions to continue to expand. The more they expand, the less likely it is for other strings to get entangled around them since it takes more energy for a string to wrap around a larger dimension. Thus, the expansion feeds on itself, becoming ever less constricted as the dimensions get ever larger. We can now imagine that these three spatial dimensions continue to evolve in the manner described in the previous sections, and expand to a size as large as or larger than the currently observable universe.
Cosmology and Calabi-Yau Shapes
For simplicity, Brandenberger and Vafa imagined that all of the spatial dimensions are circular. In fact, as noted in Chapter 8, so long as the circular dimensions are large enough that they curve back on themselves only beyond the range of our current observational capacity, a circular shape is consistent with the universe we observe. But for dimensions that stay small, a more realistic scenario is one in which they are curled up into a more intricate Calabi-Yau space. Of course, the key question is, Which Calabi-Yau space? How is this particular space determined? No one has been able to answer this question. But by combining the drastic topology-changing results described in the preceding chapter with these cosmological insights, we can suggest a framework for doing so. Through the space-tearing conifold transitions, we now know that any Calabi-Yau shape can evolve into any other. So, we can imagine that in the tumultuous, hot moments after the bang, the curled-up Calabi-Yau component of space stays small, but goes through a frenetic dance in which its fabric rips apart and reconnects over and over again, rapidly taking us through a long sequence of different Calabi-Yau shapes. As the universe cools and three of the spatial dimensions get large, the transitions from one Calabi-Yau to another slow down, with the extra dimensions ultimately settling into a Calabi-Yau shape that, optimistically, gives rise to the physical features we observe in the world around us. The challenge facing physicists is to understand, in detail, the evolution of the Calabi-Yau component of space so that its present form can be predicted from theoretical principles. With the newfound ability of one Calabi-Yau to change smoothly into another, we see that the issue of selecting one Calabi-Yau shape from the many may in fact be reduced to a problem of cosmology.5
Before the Beginning?
Lacking the exact equations of string theory, Brandenberger and Vafa were forced to make numerous approximations and assumptions in their cosmological studies. As Vafa recently said,
Our work highlights the new way in which string theory allows us to start addressing persistent problems in the standard approach to cosmology. We see, for example, that the whole notion of an initial singularity may be completely avoided by string theory. But, because of difficulties in performing fully trustworthy calculations in such extreme situations with our present understanding of string theory, our work only provides a first look into string cosmology, and is very far from the final word.6
Since their work, physicists have made steady progress in furthering the understanding of string cosmology, spearheaded by, among others, Gabriele Veneziano and his collaborator Maurizio Gasperini of the University of Torino. Gasperini and Veneziano have come up with their own intriguing version of string cosmology that shares certain features with the scenario described above, but also differs in significant ways. As in the Brandenberger and Vafa work, they too rely on string theory's having a minimal length in order to avoid the infinite temperature and energy density that arises in the standard and inflationary cosmological theories. But rather than concluding that this means the universe begins as an extremely hot Planck-size nugget, Gasperini and Veneziano suggest that there may be a whole prehistory to the universe—starting long before what we have so far been calling time zero—that leads up to the Planckian cosmic embryo.
In this so-called pre-big bang scenario, the universe began in a vastly different state than it does in the big bang framework. Gasperini and Veneziano's work suggests that rather than being enormously hot and tightly curled into a tiny spatial speck, the universe started out as cold and essentially infinite in spatial extent. The equations of string theory then indicate that—somewhat as in Guth's inflationary epoch—an instability kicked in, driving every point in the universe to rush rapidly away from every other. Gasperini and Veneziano show that this caused space to become increasingly curved and results in a dramatic increase in temperature and energy density.7 After some time, a millimeter-sized three-dimensional region within this vast expanse could look just like the super-hot and dense patch emerging from Guth's inflationary expansion. Then, through the standard expansion of ordinary big bang cosmology, this patch can account for the whole of the universe with which we are familiar. Moreover, because the pre-big bang epoch involves its own inflationary expansion, Guth's solution to the horizon problem is automatically built into the pre-big bang cosmological scenario. As Veneziano has said, "String theory offers us a version of inflationary cosmology on a silver platter."8
The study of superstring cosmology is rapidly becoming an active and fertile arena of research. The pre-big bang scenario, for example, has already generated a significant amount of heated, yet fruitful debate, and it is far from clear what role it will have in the cosmological framework that will ultimately emerge from string theory. Achieving these cosmological insights will, no doubt, rely heavily on the ability of physicists to come to grips with all aspects of the second superstring revolution. What, for example, are the cosmological consequences of the existence of fundamental higher-dimensional branes? How do the cosmological properties we have discussed change if string theory happens to have a coupling constant whose value places us more toward the center of Figure 12.11 rather than in one of the peninsular regions? That is, what is the impact of full-fledged M-theory on the earliest moments of the universe? These central questions are now being studied vigorously. Already, one important insight has emerged.
M-Theory and the Merging of All Forces
In Figure 7.1 we showed how the strengths of the three nongravitational couplings merge together when the temperature of the universe is high enough. How does the strength of the gravitational force fit into this picture? Before the emergence of M-theory, string theorists were able to show that with the simplest of choices for the Calabi-Yau component of space, the gravitational force almost, but not quite, merges with the other three, as shown in Figure 14.2. String theorists found that the mismatch could be avoided by carefully molding the shape of the chosen Calabi-Yau, among other tricks of the trade, but such after-the-fact fine tuning always makes a physicist uncomfortable. Since no one currently knows how to predict the precise form of the Calabi-Yau dimensions, it seems dangerous to rely upon solutions to problems that hinge so delicately on the fine details of their shape.
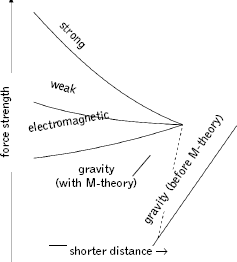
Figure 14.2 Within M-theory, the strengths of all four forces can naturally merge.
Witten has shown, however, that the second superstring revolution provides a far more robust solution. By investigating how the strengths of the forces vary when the string coupling constant is not necessarily small, Witten found that the gravitational force curve can be gently nudged to merge with the other forces, as in Figure 14.2, without any special molding of the Calabi-Yau portion of space. Although it is far too early to tell, this may indicate that cosmological unity is more easily achieved by making use of the larger framework of M-theory.
The developments discussed in this and the previous sections represent the first, somewhat tentative steps toward understanding the cosmological implications of string/M-theory. During the coming years, as the nonperturbative tools of string/M-theory are sharpened, physicists anticipate that some of the most profound insights will emerge from their application to cosmological questions.
But without currently having methods that are sufficiently powerful to understand cosmology according to string theory fully, it is worthwhile to think about some general considerations concerning the possible role of cosmology in the search for the ultimate theory. We caution that some of these ideas are of a more speculative nature than much of what we have discussed previously, but they do raise issues that any purported final theory may one day have to address.
Cosmological Speculation and the Ultimate Theory
Cosmology has the ability to grab hold of us at a deep, visceral level because an understanding of how things began feels—at least to some—like the closest we may ever come to understanding why they began. That is not to say that modern science provides a connection between the question of how and the question of why—it doesn't—and it may well be that no such scientific connection is ever found. But the study of cosmology does hold the promise of giving us our most complete understanding of the arena of the why—the birth of the universe—and this at least allows for a scientifically informed view of the frame within which the questions are asked. Sometimes attaining the deepest familiarity with a question is our best substitute for actually having the answer.
In the context of searching for the ultimate theory, these lofty reflections on cosmology give way to far more concrete considerations. The way things in the universe appear to us today—way on the far right-hand side of the time line in Figure 14.1—depends upon the fundamental laws of physics, to be sure, but it may also depend on aspects of cosmological evolution, from the far left-hand side of the time line, that potentially lie outside the scope of even the deepest theory.
It's not hard to imagine how this might be. Think of what happens, for example, when you toss a ball in the air. The laws of gravity govern the ball's subsequent motion, but we can't predict where the ball will land exclusively from those laws. We must also know the velocity of the ball—its speed and direction—as it left your hand. That is, we must know the initial conditions of the ball's motion. Similarly, there are features of the universe that also have a historical contingency—the reason why a star formed here or a planet there depends upon a complicated chain of events that, at least in principle, we can imagine tracing back to some feature of how the universe was when it all began. But it is possible that even more basic features of the universe, perhaps even the properties of the fundamental matter and force particles, also have a direct dependence on historical evolution—evolution that itself is contingent upon the initial conditions of the universe.
In fact, we've already noted one possible incarnation of this idea in string theory: As the hot, early universe evolved, the extra dimensions may have transmuted from shape to shape, ultimately settling down to one particular Calabi-Yau space once things had cooled off sufficiently. But, like a ball tossed in the air, the result of that journey through numerous Calabi-Yau shapes may well depend on details of how the journey got started in the first place. And through the influence of the resulting Calabi-Yau shape on particle masses and on properties of forces, we see that cosmological evolution and the state of the universe when it began can have a profound impact on the physics we currently observe.
We don't know what the initial conditions of the universe were, or even the ideas, concepts, and language that should be used to describe them. We believe that the outrageous initial state of infiniteenergy, density, and temperature that arises in the standard and inflationary cosmological models is a signal that these theories have broken down rather than a correct description of the physical conditions that actually existed. String theory offers an improvement by showing how such infinite extremes might be avoided; nevertheless, no one has any insight on the question of how things actually did begin. In fact, our ignorance persists on an even higher plane: We don't know whether the question of determining the initial conditions is one that is even sensible to ask or whether—like asking general relativity to give insight into how hard you happened to toss a ball in the air—it is a question that lies forever beyond the grasp of any theory. Valiant attempts by physicists such as Hawking and James Hartle of the University of California at Santa Barbara have tried to bring the question of cosmological initial conditions within the umbrella of physical theory, but all such attempts remain inconclusive. In the context of string/M-theory, our cosmological understanding is, at present, just too primitive to determine whether our candidate "theory of everything" truly lives up to its name and determines its own cosmological initial conditions, thereby elevating them to the status of physical law. This is a prime question for future research.
But even beyond the issue of initial conditions and their impact on the ensuing historical twists and turns of cosmic evolution, some recent and highly speculative proposals have argued for yet other potential limits on the explanatory power of any final theory. No one knows if these ideas are right or wrong, and certainly they currently lie on the outskirts of mainstream science. But they do highlight—albeit in a rather provocative and speculative manner—an obstacle that any proposed final theory may encounter.
The basic idea rests upon the following possibility. Imagine that what we call the universe is actually only one tiny part of a vastly larger cosmological expanse, one of an enormous number of island universes scattered across a grand cosmological archipelago. Although this might sound rather far-fetched—and in the end it may well be—Andrei Linde has suggested a concrete mechanism that might lead to such a gargantuan universe. Linde has found that the brief but crucial burst of inflationary expansion discussed earlier may not have been a unique, one-time event. Instead, he argues, the conditions for inflationary expansion may happen repeatedly in isolated regions peppered throughout the cosmos, which then undergo their own inflationary ballooning in size, evolving into new, separate universes. And in each of these universes, the process continues, with new universes sprouting from far-flung regions in the old, generating a never ending web of ballooning cosmic expanses. The terminology gets a little cumbersome, but let's follow fashion and call this greatly expanded notion of the universe the multiverse, with each of the constituent parts being called a universe.
The central observation is that whereas in Chapter 7 we noted that everything we know points toward a consistent and uniform physics throughout our universe, this may have no bearing on the physical attributes in these other universes so long as they are separate from us, or at least so far away that their light has not had time to reach us. And so we can imagine that physics varies from one universe to another. In some, the differences may be subtle: For example, the electron mass or the strength of the strong force might be a thousandth of a percent larger or smaller than in our universe. In others, physics may differ in more pronounced ways: The up-quark might weigh ten times what it weighs in our universe, or the strength of the electromagnetic force might be ten times the value we measure, with all the profound implications that this has on stars and on life as we know it (as indicated in Chapter 1). And in other universes, physics may differ in still more dramatic ways: The list of elementary particles and forces may be completely distinct from ours, or, taking a cue from string theory, even the number of extended dimensions may differ, with some cramped universes having as few as zero or one large spatial dimension, while other expansive universes possess eight, nine, or even ten extended spatial dimensions. If we let our imaginations run free, even the laws themselves can drastically differ from universe to universe. The range of possibilities is endless.
Here's the point. If we scan through this huge maze of universes, the vast majority will not have conditions hospitable to life, or at least to anything remotely akin to life as we know it. For drastic changes in familiar physics, this is clear: If our universe truly looked like the Garden-hose universe, life as we know it would not exist. But even rather conservative changes to physics would interfere with the formation of stars, for example, disrupting their ability to act as cosmic furnaces that synthesize complex life-supporting atoms such as carbon and oxygen that, normally, are spewed throughout the universe by supernova explosions. In light of the sensitive dependence of life on the details of physics, if we now ask, for instance, why the forces and particles of nature have the particular properties we observe, a possible answer emerges: Across the entire multiverse, these features vary widely; their properties can be different and are different in other universes. What's special about the particular combination of particle and force properties we observe is that, clearly, they allow life to form. And life, intelligent life in particular, is a prerequisite even to ask the question of why our universe has the properties it does. In plain language, things are the way they are in our universe because if they weren't, we wouldn't be here to notice. Like the winners of a mass game of Russian roulette, whose surprise at surviving is tempered by the realization that had they not won, they wouldn't have been able not to feel surprised, the multiverse hypothesis has the capacity to lessen our insistence on explaining why our universe appears as it does.
This line of argument is a version of an idea with a long history known as the anthropic principle. As presented, it is a perspective that is diametrically opposed to the dream of a rigid, fully predictive, unified theory in which things are the way they are because the universe could not be otherwise. Rather than being the epitome of poetic grace in which everything fits together with inflexible elegance, the multiverse and the anthropic principle paint a picture of a wildly excessive collection of universes with an insatiable appetite for variety. It will be extremely hard, if not impossible, for us ever to know if the multiverse picture is true. Even if there are other universes, we can imagine that we will never come into contact with any of them. But by vastly increasing the scope of "what's out there"—in a manner that dwarfs Hubble's realization that the Milky Way is but one galaxy among many—the concept of the multiverse does at least alert us to the possibility that we may be asking too much of an ultimate theory.
We should require that our ultimate theory give a quantum-mechanically consistent description of all forces and all matter. We should require that our ultimate theory give a cogent cosmology within our universe. However, if the multiverse picture is correct—a huge if—it may be asking too much for our theory to explain, as well, the detailed properties of the particle masses, charges, and the force strengths.
But we must emphasize that even if we accept the speculative premise of the multiverse, the conclusion that this compromises our predictive power is far from airtight. The reason, simply put, is that if we unleash our imaginations and allow ourselves to contemplate a multiverse, we should also unleash our theoretical musings and contemplate ways in which the apparent randomness of the multiverse can be tamed. For one relatively conservative musing, we can imagine that—were the multiverse picture true—we would be able to extend our ultimate theory to its full sprawling expanse, and that our "extended ultimate theory" might tell us precisely why and how the values of the fundamental parameters are sprinkled across the constituent universes.
A more radical musing comes from a proposal of Lee Smolin of Penn State University, who, inspired by the similarity between conditions at the big bang and at the centers of black holes—each being characterized by a colossal density of crushed matter—has suggested that every black hole is the seed for a new universe that erupts into existence through a big bang-like explosion, but is forever hidden from our view by the black hole's event horizon. Beyond proposing another mechanism for generating a multiverse, Smolin has injected a new element—a cosmic version of genetic mutation—that does an end run around the scientific limitations associated with the anthropic principle.9 Imagine, he suggests, that when a universe sprouts from the core of a black hole, its physical attributes, such as particle masses and force strengths, are close, but not identical, to those of its parent universe. Since black holes arise from extinguished stars, and star formation depends upon the precise values of the particle masses and force strengths, the fecundity of any given universe—the number of black hole progeny it can produce—depends sensitively on these parameters. Small variations in the parameters of the progeny universes will therefore lead to some that are even more optimized for black hole production than their parent universe, and have an even greater number of offspring universes of their own.10 After many "generations," the descendants of universes optimized for producing black holes will thus be so numerous that they will overwhelm the population of the multiverse. And so, rather than invoking the anthropic principle, Smolin's suggestion provides a dynamic mechanism that, on average, drives the parameters of each next-generation universe ever closer to particular values—those that are optimum for black hole production.
This approach gives another method, even in the context of the multiverse, in which the fundamental matter and force parameters can be explained. If Smolin's theory is right, and if we are a typical member of a mature multiverse (these are big "ifs" and can be debated on many fronts, of course), the parameters of the particles and forces that we measure should be optimized for black hole production. That is, any fiddling with these parameters of our universe should make it harder for black holes to form. Physicists have begun to investigate this prediction; at present there is no consensus on its validity. But even if Smolin's specific proposal turns out to be wrong, it does present yet another shape that the ultimate theory might take. The ultimate theory may, at first sight, appear to lack rigidity. We may find that it can describe a wealth of universes, most of which have no relevance to the one we inhabit. And moreover, we can imagine that this wealth of universes may be physically realized, leading to a multiverse—something that, at first sight, forever limits our predictive power. In fact, however, this discussion illustrates that an ultimate explanation can yet be achieved, so long as we grasp not only the ultimate laws but also their implications for cosmological evolution on an unexpectedly grand scale.
Undoubtedly, the cosmological implications of string/M-theory will be a major field of study well into the twenty-first century. Without accelerators capable of producing Planck-scale energies, we will increasingly have to rely on the cosmological accelerator of the big bang, and the relics it has left for us throughout the universe, for our experimental data. With luck and perseverance, we may finally be able to answer questions such as how the universe began, and why it has evolved to the form we behold in the heavens and on earth. There is, of course, much uncharted territory between where we are and where full answers to these fundamental questions lie. But the development of a quantum theory of gravity through superstring theory lends credence to the hope that we now possess theoretical tools for pushing into the vast regions of the unknown, and, no doubt after many a struggle, possibly emerging with answers to some of the deepest questions ever posed.