Chaos: Making a New Science - James Gleick (1988)

The Butterfly Effect

Physicists like to think that all you have to do is say, these are the conditions, now what happens next?

—RICHARD P. FEYNMAN

THE SUN BEAT DOWN through a sky that had never seen clouds. The winds swept across an earth as smooth as glass. Night never came, and autumn never gave way to winter. It never rained. The simulated weather in Edward Lorenz’s new electronic computer changed slowly but certainly, drifting through a permanent dry midday midseason, as if the world had turned into Camelot, or some particularly bland version of southern California.

Outside his window Lorenz could watch real weather, the early-morning fog creeping along the Massachusetts Institute of Technology campus or the low clouds slipping over the rooftops from the Atlantic. Fog and clouds never arose in the model running on his computer. The machine, a Royal McBee, was a thicket of wiring and vacuum tubes that occupied an ungainly portion of Lorenz’s office, made a surprising and irritating noise, and broke down every week or so. It had neither the speed nor the memory to manage a realistic simulation of the earth’s atmosphere and oceans. Yet Lorenz created a toy weather in 1960 that succeeded in mesmerizing his colleagues. Every minute the machine marked the passing of a day by printing a row of numbers across a page. If you knew how to read the printouts, you would see a prevailing westerly wind swing now to the north, now to the south, now back to the north. Digitized cyclones spun slowly around an idealized globe. As word spread through the department, the other meteorologists would gather around with the graduate students, making bets on what Lorenz’s weather would do next. Somehow, nothing ever happened the same way twice.

Lorenz enjoyed weather—by no means a prerequisite for a research meteorologist. He savored its changeability. He appreciated the patterns that come and go in the atmosphere, families of eddies and cyclones, always obeying mathematical rules, yet never repeating themselves. When he looked at clouds, he thought he saw a kind of structure in them. Once he had feared that studying the science of weather would be like prying a jack-in-the-box apart with a screwdriver. Now he wondered whether science would be able to penetrate the magic at all. Weather had a flavor that could not be expressed by talking about averages. The daily high temperature in Cambridge, Massachusetts, averages 75 degrees in June. The number of rainy days in Riyadh, Saudi Arabia, averages ten a year. Those were statistics. The essence was the way patterns in the atmosphere changed over time, and that was what Lorenz captured on the Royal McBee.

He was the god of this machine universe, free to choose the laws of nature as he pleased. After a certain amount of undivine trial and error, he chose twelve. They were numerical rules—equations that expressed the relationships between temperature and pressure, between pressure and wind speed. Lorenz understood that he was putting into practice the laws of Newton, appropriate tools for a clockmaker deity who could create a world and set it running for eternity. Thanks to the determinism of physical law, further intervention would then be unnecessary. Those who made such models took for granted that, from present to future, the laws of motion provide a bridge of mathematical certainty. Understand the laws and you understand the universe. That was the philosophy behind modeling weather on a computer.

Indeed, if the eighteenth-century philosophers imagined their creator as a benevolent noninterventionist, content to remain behind the scenes, they might have imagined someone like Lorenz. He was an odd sort of meteorologist. He had the worn face of a Yankee farmer, with surprising bright eyes that made him seem to be laughing whether he was or not. He seldom spoke about himself or his work, but he listened. He often lost himself in a realm of calculation or dreaming that his colleagues found inaccessible. His closest friends felt that Lorenz spent a good deal of his time off in a remote outer space.

As a boy he had been a weather bug, at least to the extent of keeping close tabs on the max-min thermometer recording the days’ highs and lows outside his parents’ house in West Hartford, Connecticut. But he spent more time inside playing with mathematical puzzle books than watching the thermometer. Sometimes he and his father would work out puzzles together. Once they came upon a particularly difficult problem that turned out to be insoluble. That was acceptable, his father told him: you can always try to solve a problem by proving that no solution exists. Lorenz liked that, as he always liked the purity of mathematics, and when he graduated from Dartmouth College, in 1938, he thought that mathematics was his calling. Circumstance interfered, however, in the form of World War II, which put him to work as a weather forecaster for the Army Air Corps. After the war Lorenz decided to stay with meteorology, investigating the theory of it, pushing the mathematics a little further forward. He made a name for himself by publishing work on orthodox problems, such as the general circulation of the atmosphere. And in the meantime he continued to think about forecasting.

To most serious meteorologists, forecasting was less than science. It was a seat-of-the-pants business performed by technicians who needed some intuitive ability to read the next day’s weather in the instruments and the clouds. It was guesswork. At centers like M.I.T., meteorology favored problems that had solutions. Lorenz understood the messiness of weather prediction as well as anyone, having tried it firsthand for the benefit of military pilots, but he harbored an interest in the problem—a mathematical interest.

Not only did meteorologists scorn forecasting, but in the 1960s virtually all serious scientists mistrusted computers. These souped-up calculators hardly seemed like tools for theoretical science. So numerical weather modeling was something of a bastard problem. Yet the time was right for it. Weather forecasting had been waiting two centuries for a machine that could repeat thousands of calculations over and over again by brute force. Only a computer could cash in the Newtonian promise that the world unfolded along a deterministic path, rule-bound like the planets, predictable like eclipses and tides. In theory a computer could let meteorologists do what astronomers had been able to do with pencil and slide rule: reckon the future of their universe from its initial conditions and the physical laws that guide its evolution. The equations describing the motion of air and water were as well known as those describing the motion of planets. Astronomers did not achieve perfection and never would, not in a solar system tugged by the gravities of nine planets, scores of moons and thousands of asteroids, but calculations of planetary motion were so accurate that people forgot they were forecasts. When an astronomer said, “Comet Halley will be back this way in seventy-six years,” it seemed like fact, not prophecy. Deterministic numerical forecasting figured accurate courses for spacecraft and missiles. Why not winds and clouds?

Weather was vastly more complicated, but it was governed by the same laws. Perhaps a powerful enough computer could be the supreme intelligence imagined by Laplace, the eighteenth-century philosopher-mathematician who caught the Newtonian fever like no one else: “Such an intelligence,” Laplace wrote, “would embrace in the same formula the movements of the greatest bodies of the universe and those of the lightest atom; for it, nothing would be uncertain and the future, as the past, would be present to its eyes.” In these days of Einstein’s relativity and Heisenberg’s uncertainty, Laplace seems almost buffoon-like in his optimism, but much of modern science has pursued his dream. Implicitly, the mission of many twentieth-century scientists—biologists, neurologists, economists—has been to break their universes down into the simplest atoms that will obey scientific rules. In all these sciences, a kind of Newtonian determinism has been brought to bear. The fathers of modern computing always had Laplace in mind, and the history of computing and the history of forecasting were intermingled ever since John von Neumann designed his first machines at the Institute for Advanced Study in Princeton, New Jersey, in the 1950s. Von Neumann recognized that weather modeling could be an ideal task for a computer.

There was always one small compromise, so small that working scientists usually forgot it was there, lurking in a corner of their philosophies like an unpaid bill. Measurements could never be perfect. Scientists marching under Newton’s banner actually waved another flag that said something like this: Given an approximate knowledge of a system’s initial conditions and an understanding of natural law, one can calculate the approximate behavior of the system. This assumption lay at the philosophical heart of science. As one theoretician liked to tell his students: “The basic idea of Western science is that you don’t have to take into account the falling of a leaf on some planet in another galaxy when you’re trying to account for the motion of a billiard ball on a pool table on earth. Very small influences can be neglected. There’s a convergence in the way things work, and arbitrarily small influences don’t blow up to have arbitrarily large effects.” Classically, the belief in approximation and convergence was well justified. It worked. A tiny error in fixing the position of Comet Halley in 1910 would only cause a tiny error in predicting its arrival in 1986, and the error would stay small for millions of years to come. Computers rely on the same assumption in guiding spacecraft: approximately accurate input gives approximately accurate output. Economic forecasters rely on this assumption, though their success is less apparent. So did the pioneers in global weather forecasting.

With his primitive computer, Lorenz had boiled weather down to the barest skeleton. Yet, line by line, the winds and temperatures in Lorenz’s printouts seemed to behave in a recognizable earthly way. They matched his cherished intuition about the weather, his sense that it repeated itself, displaying familiar patterns over time, pressure rising and falling, the airstream swinging north and south. He discovered that when a line went from high to low without a bump, a double bump would come next, and he said, “That’s the kind of rule a forecaster could use.” But the repetitions were never quite exact. There was pattern, with disturbances. An orderly disorder.

To make the patterns plain to see, Lorenz created a primitive kind of graphics. Instead of just printing out the usual lines of digits, he would have the machine print a certain number of blank spaces followed by the letter a. He would pick one variable—perhaps the direction of the airstream. Gradually the a’s marched down the roll of paper, swinging back and forth in a wavy line, making a long series of hills and valleys that represented the way the west wind would swing north and south across the continent. The orderliness of it, the recognizable cycles coming around again and again but never twice the same way, had a hypnotic fascination. The system seemed slowly to be revealing its secrets to the forecaster’s eye.

One day in the winter of 1961, wanting to examine one sequence at greater length, Lorenz took a shortcut. Instead of starting the whole run over, he started midway through. To give the machine its initial conditions, he typed the numbers straight from the earlier printout. Then he walked down the hall to get away from the noise and drink a cup of coffee. When he returned an hour later, he saw something unexpected, something that planted a seed for a new science.

THIS NEW RUN should have exactly duplicated the old. Lorenz had copied the numbers into the machine himself. The program had not changed. Yet as he stared at the new printout, Lorenz saw his weather diverging so rapidly from the pattern of the last run that, within just a few months, all resemblance had disappeared. He looked at one set of numbers, then back at the other. He might as well have chosen two random weathers out of a hat. His first thought was that another vacuum tube had gone bad.

Suddenly he realized the truth. There had been no malfunction. The problem lay in the numbers he had typed. In the computer’s memory, six decimal places were stored: .506127. On the printout, to save space, just three appeared: .506. Lorenz had entered the shorter, rounded-off numbers, assuming that the difference—one part in a thousand—was inconsequential.

It was a reasonable assumption. If a weather satellite can read ocean-surface temperature to within one part in a thousand, its operators consider themselves lucky. Lorenz’s Royal McBee was implementing the classical program. It used a purely deterministic system of equations. Given a particular starting point, the weather would unfold exactly the same way each time. Given a slightly different starting point, the weather should unfold in a slightly different way. A small numerical error was like a small puff of wind—surely the small puffs faded or canceled each other out before they could change important, large-scale features of the weather. Yet in Lorenz’s particular system of equations, small errors proved catastrophic.

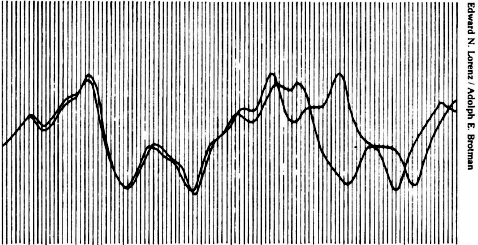
HOW TWO WEATHER PATTERNS DIVERGE. From nearly the same starting point, Edward Lorenz saw his computer weather produce patterns that grew farther and farther apart until all resemblance disappeared. (From Lorenz’s 1961 printouts.)

He decided to look more closely at the way two nearly identical runs of weather flowed apart. He copied one of the wavy lines of output onto a transparency and laid it over the other, to inspect the way it diverged. First, two humps matched detail for detail. Then one line began to lag a hairsbreadth behind. By the time the two runs reached the next hump, they were distinctly out of phase. By the third or fourth hump, all similarity had vanished.

It was only a wobble from a clumsy computer. Lorenz could have assumed something was wrong with his particular machine or his particular model—probably should have assumed. It was not as though he had mixed sodium and chlorine and got gold. But for reasons of mathematical intuition that his colleagues would begin to understand only later, Lorenz felt a jolt: something was philosophically out of joint. The practical import could be staggering. Although his equations were gross parodies of the earth’s weather, he had a faith that they captured the essence of the real atmosphere. That first day, he decided that long-range weather forecasting must be doomed.

“We certainly hadn’t been successful in doing that anyway and now we had an excuse,” he said. “I think one of the reasons people thought it would be possible to forecast so far ahead is that there are real physical phenomena for which one can do an excellent job of forecasting, such as eclipses, where the dynamics of the sun, moon, and earth are fairly complicated, and such as oceanic tides. I never used to think of tide forecasts as prediction at all—I used to think of them as statements of fact—but of course, you are predicting. Tides are actually just as complicated as the atmosphere. Both have periodic components—you can predict that next summer will be warmer than this winter. But with weather we take the attitude that we knew that already. With tides, it’s the predictable part that we’re interested in, and the unpredictable part is small, unless there’s a storm.

“The average person, seeing that we can predict tides pretty well a few months ahead would say, why can’t we do the same thing with the atmosphere, it’s just a different fluid system, the laws are about as complicated. But I realized that any physical system that behaved nonperiodically would be unpredictable.”

THE FIFTIES AND SIXTIES were years of unreal optimism about weather forecasting. Newspapers and magazines were filled with hope for weather science, not just for prediction but for modification and control. Two technologies were maturing together, the digital computer and the space satellite. An international program was being prepared to take advantage of them, the Global Atmosphere Research Program. There was an idea that human society would free itself from weather’s turmoil and become its master instead of its victim. Geodesic domes would cover cornfields. Airplanes would seed the clouds. Scientists would learn how to make rain and how to stop it.

The intellectual father of this popular notion was Von Neumann, who built his first computer with the precise intention, among other things, of controlling the weather. He surrounded himself with meteorologists and gave breathtaking talks about his plans to the general physics community. He had a specific mathematical reason for his optimism. He recognized that a complicated dynamical system could have points of instability—critical points where a small push can have large consequences, as with a ball balanced at the top of a hill. With the computer up and running, Von Neumann imagined that scientists would calculate the equations of fluid motion for the next few days. Then a central committee of meteorologists would send up airplanes to lay down smoke screens or seed clouds to push the weather into the desired mode. But Von Neumann had overlooked the possibility of chaos, with instability at every point.

By the 1980s a vast and expensive bureaucracy devoted itself to carrying out Von Neumann’s mission, or at least the prediction part of it. America’s premier forecasters operated out of an unadorned cube of a building in suburban Maryland, near the Washington beltway, with a spy’s nest of radar and radio antennas on the roof. Their supercomputer ran a model that resembled Lorenz’s only in its fundamental spirit. Where the Royal McBee could carry out sixty multiplications each second, the speed of a Control Data Cyber 205 was measured in megaflops, millions of floating-point operations per second. Where Lorenz had been happy with twelve equations, the modern global model calculated systems of 500,000 equations. The model understood the way moisture moved heat in and out of the air when it condensed and evaporated. The digital winds were shaped by digital mountain ranges. Data poured in hourly from every nation on the globe, from airplanes, satellites, and ships. The National Meteorological Center produced the world’s second best forecasts.

The best came out of Reading, England, a small college town an hour’s drive from London. The European Centre for Medium Range Weather Forecasts occupied a modest tree-shaded building in a generic United Nations style, modern brick-and-glass architecture, decorated with gifts from many lands. It was built in the heyday of the all-European Common Market spirit, when most of the nations of western Europe decided to pool their talent and resources in the cause of weather prediction. The Europeans attributed their success to their young, rotating staff—no civil service—and their Cray supercomputer, which always seemed to be one model ahead of the American counterpart.

Weather forecasting was the beginning but hardly the end of the business of using computers to model complex systems. The same techniques served many kinds of physical scientists and social scientists hoping to make predictions about everything from the small-scale fluid flows that concerned propeller designers to the vast financial flows that concerned economists. Indeed, by the seventies and eighties, economic forecasting by computer bore a real resemblance to global weather forecasting. The models would churn through complicated, somewhat arbitrary webs of equations, meant to turn measurements of initial conditions—atmospheric pressure or money supply—into a simulation of future trends. The programmers hoped the results were not too grossly distorted by the many unavoidable simplifying assumptions. If a model did anything too obviously bizarre—flooded the Sahara or tripled interest rates—the programmers would revise the equations to bring the output back in line with expectation. In practice, econometric models proved dismally blind to what the future would bring, but many people who should have known better acted as though they believed in the results. Forecasts of economic growth or unemployment were put forward with an implied precision of two or three decimal places. Governments and financial institutions paid for such predictions and acted on them, perhaps out of necessity or for want of anything better. Presumably they knew that such variables as “consumer optimism” were not as nicely measurable as “humidity” and that the perfect differential equations had not yet been written for the movement of politics and fashion. But few realized how fragile was the very process of modeling flows on computers, even when the data was reasonably trustworthy and the laws were purely physical, as in weather forecasting.

Computer modeling had indeed succeeded in changing the weather business from an art to a science. The European Centre’s assessments suggested that the world saved billions of dollars each year from predictions that were statistically better than nothing. But beyond two or three days the world’s best forecasts were speculative, and beyond six or seven they were worthless.

The Butterfly Effect was the reason. For small pieces of weather—and to a global forecaster, small can mean thunderstorms and blizzards—any prediction deteriorates rapidly. Errors and uncertainties multiply, cascading upward through a chain of turbulent features, from dust devils and squalls up to continent-size eddies that only satellites can see.

The modern weather models work with a grid of points on the order of sixty miles apart, and even so, some starting data has to be guessed, since ground stations and satellites cannot see everywhere. But suppose the earth could be covered with sensors spaced one foot apart, rising at one-foot intervals all the way to the top of the atmosphere. Suppose every sensor gives perfectly accurate readings of temperature, pressure, humidity, and any other quantity a meteorologist would want. Precisely at noon an infinitely powerful computer takes all the data and calculates what will happen at each point at 12:01, then 12:02, then 12:03…

The computer will still be unable to predict whether Princeton, New Jersey, will have sun or rain on a day one month away. At noon the spaces between the sensors will hide fluctuations that the computer will not know about, tiny deviations from the average. By 12:01, those fluctuations will already have created small errors one foot away. Soon the errors will have multiplied to the ten-foot scale, and so on up to the size of the globe.

Even for experienced meteorologists, all this runs against intuition. One of Lorenz’s oldest friends was Robert White, a fellow meteorologist at M.I.T. who later became head of the National Oceanic and Atmospheric Administration. Lorenz told him about the Butterfly Effect and what he felt it meant for long-range prediction. White gave Von Neumann’s answer. “Prediction, nothing,” he said. “This is weather control.” His thought was that small modifications, well within human capability, could cause desired large-scale changes.

Lorenz saw it differently. Yes, you could change the weather. You could make it do something different from what it would otherwise have done. But if you did, then you would never know what it would otherwise have done. It would be like giving an extra shuffle to an already well-shuffled pack of cards. You know it will change your luck, but you don’t know whether for better or worse.

LORENZ’S DISCOVERY WAS AN ACCIDENT, one more in a line stretching back to Archimedes and his bathtub. Lorenz never was the type to shout Eureka. Serendipity merely led him to a place he had been all along. He was ready to explore the consequences of his discovery by working out what it must mean for the way science understood flows in all kinds of fluids.

Had he stopped with the Butterfly Effect, an image of predictability giving way to pure randomness, then Lorenz would have produced no more than a piece of very bad news. But Lorenz saw more than randomness embedded in his weather model. He saw a fine geometrical structure, order masquerading as randomness. He was a mathematician in meteorologist’s clothing, after all, and now he began to lead a double life. He would write papers that were pure meteorology. But he would also write papers that were pure mathematics, with a slightly misleading dose of weather talk as preface. Eventually the prefaces would disappear altogether.

He turned his attention more and more to the mathematics of systems that never found a steady state, systems that almost repeated themselves but never quite succeeded. Everyone knew that the weather was such a system—aperiodic. Nature is full of others: animal populations that rise and fall almost regularly, epidemics that come and go on tantalizingly near-regular schedules. If the weather ever did reach a state exactly like one it had reached before, every gust and cloud the same, then presumably it would repeat itself forever after and the problem of forecasting would become trivial.

Lorenz saw that there must be a link between the unwillingness of the weather to repeat itself and the inability of forecasters to predict it—a link between aperiodicity and unpredictability. It was not easy to find simple equations that would produce the aperiodicity he was seeking. At first his computer tended to lock into repetitive cycles. But Lorenz tried different sorts of minor complications, and he finally succeeded when he put in an equation that varied the amount of heating from east to west, corresponding to the real-world variation between the way the sun warms the east coast of North America, for example, and the way it warms the Atlantic Ocean. The repetition disappeared.

The Butterfly Effect was no accident; it was necessary. Suppose small perturbations remained small, he reasoned, instead of cascading upward through the system. Then when the weather came arbitrarily close to a state it had passed through before, it would stay arbitrarily close to the patterns that followed. For practical purposes, the cycles would be predictable—and eventually uninteresting. To produce the rich repertoire of real earthly weather, the beautiful multiplicity of it, you could hardly wish for anything better than a Butterfly Effect.

The Butterfly Effect acquired a technical name: sensitive dependence on initial conditions. And sensitive dependence on initial conditions was not an altogether new notion. It had a place in folklore:

“For want of a nail, the shoe was lost;

For want of a shoe, the horse was lost;

For want of a horse, the rider was lost;

For want of a rider, the battle was lost;

For want of a battle, the kingdom was lost!”

In science as in life, it is well known that a chain of events can have a point of crisis that could magnify small changes. But chaos meant that such points were everywhere. They were pervasive. In systems like the weather, sensitive dependence on initial conditions was an inescapable consequence of the way small scales intertwined with large.

His colleagues were astonished that Lorenz had mimicked both aperiodicity and sensitive dependence on initial conditions in his toy version of the weather: twelve equations, calculated over and over again with ruthless mechanical efficiency. How could such richness, such unpredictability—such chaos—arise from a simple deterministic system?

LORENZ PUT THE WEATHER ASIDE and looked for even simpler ways to produce this complex behavior. He found one in a system of just three equations. They were nonlinear, meaning that they expressed relationships that were not strictly proportional. Linear relationships can be captured with a straight line on a graph. Linear relationships are easy to think about: the more the merrier. Linear equations are solvable, which makes them suitable for textbooks. Linear systems have an important modular virtue: you can take them apart, and put them together again—the pieces add up.

Nonlinear systems generally cannot be solved and cannot be added together. In fluid systems and mechanical systems, the nonlinear terms tend to be the features that people want to leave out when they try to get a good, simple understanding. Friction, for example. Without friction a simple linear equation expresses the amount of energy you need to accelerate a hockey puck. With friction the relationship gets complicated, because the amount of energy changes depending on how fast the puck is already moving. Nonlinearity means that the act of playing the game has a way of changing the rules. You cannot assign a constant importance to friction, because its importance depends on speed. Speed, in turn, depends on friction. That twisted changeability makes nonlinearity hard to calculate, but it also creates rich kinds of behavior that never occur in linear systems. In fluid dynamics, everything boils down to one canonical equation, the Navier-Stokes equation. It is a miracle of brevity, relating a fluid’s velocity, pressure, density, and viscosity, but it happens to be nonlinear. So the nature of those relationships often becomes impossible to pin down. Analyzing the behavior of a nonlinear equation like the Navier-Stokes equation is like walking through a maze whose walls rearrange themselves with each step you take. As Von Neumann himself put it: “The character of the equation…changes simultaneously in all relevant respects: Both order and degree change. Hence, bad mathematical difficulties must be expected.” The world would be a different place—and science would not need chaos—if only the Navier-Stokes equation did not contain the demon of nonlinearity.

A particular kind of fluid motion inspired Lorenz’s three equations: the rising of hot gas or liquid, known as convection. In the atmosphere, convection stirs air heated by the sun-baked earth, and shimmering convective waves rise ghost-like above hot tar and radiators. Lorenz was just as happy talking about convection in a cup of hot coffee. As he put it, this was just one of the innumerable hydrodynamical processes in our universe whose future behavior we might wish to predict. How can we calculate how quickly a cup of coffee will cool? If the coffee is just warm, its heat will dissipate without any hydrodynamic motion at all. The coffee remains in a steady state. But if it is hot enough, a convective overturning will bring hot coffee from the bottom of the cup up to the cooler surface. Convection in coffee becomes plainly visible when a little cream is dribbled into the cup. The swirls can be complicated. But the long-term destiny of such a system is obvious. Because the heat dissipates, and because friction slows a moving fluid, the motion must come to an inevitable stop. Lorenz drily told a gathering of scientists, “We might have trouble forecasting the temperature of the coffee one minute in advance, but we should have little difficulty in forecasting it an hour ahead.” The equations of motion that govern a cooling cup of coffee must reflect the system’s destiny. They must be dissi-pative. Temperature must head for the temperature of the room, and velocity must head for zero.

Lorenz took a set of equations for convection and stripped it to the bone, throwing out everything that could possibly be extraneous, making it unrealistically simple. Almost nothing remained of the original model, but he did leave the nonlinearity. To the eye of a physicist, the equations looked easy. You would glance at them—many scientists did, in years to come—and say, I could solve that.

“Yes,” Lorenz said quietly, “there is a tendency to think that when you see them. There are some nonlinear terms in them, but you think there must be a way to get around them. But you just can’t.”

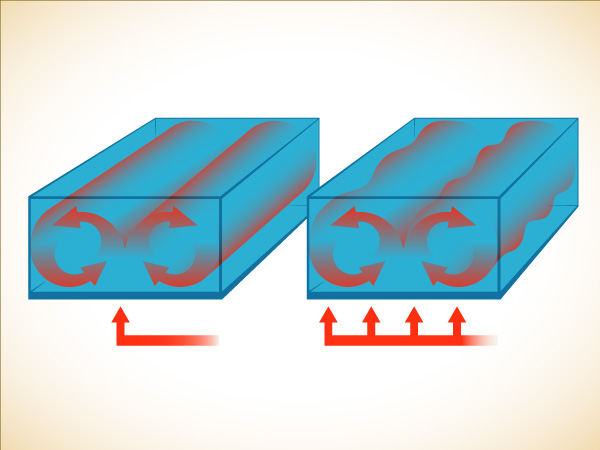
A ROLLING FLUID. When a liquid or gas is heated from below, the fluid tends to organize itself into cylindrical rolls (left). Hot fluid rises on one side, loses heat, and descends on the other side—the process of convection. When the heat is turned up further (right), an instability sets in, and the rolls develop a wobble that moves back and forth along the length of the cylinders. At even higher temperatures, the flow becomes wild and turbulent.

The simplest kind of textbook convection takes place in a cell of fluid, a box with a smooth bottom that can be heated and a smooth top that can be cooled. The temperature difference between the hot bottom and the cool top controls the flow. If the difference is small, the system remains still. Heat moves toward the top by conduction, as if through a bar of metal, without overcoming the natural tendency of the fluid to remain at rest. Furthermore, the system is stable. Any random motions that might occur when, say, a graduate student knocks into the apparatus will tend to die out, returning the system to its steady state.

Turn up the heat, though, and a new kind of behavior develops. As the fluid underneath becomes hot, it expands. As it expands, it becomes less dense. As it becomes less dense, it becomes lighter, enough to overcome friction, and it pushes up toward the surface. In a carefully designed box, a cylindrical roll develops, with the hot fluid rising around one side and cool fluid sinking down around the other. Viewed from the side, the motion makes a continuous circle. Out of the laboratory, too, nature often makes its own convection cells. When the sun heats a desert floor, for example, the rolling air can shape shadowy patterns in the clouds above or the sand below.

Turn up the heat even more, and the behavior grows more complex. The rolls begin to wobble. Lorenz’s pared-down equations were far too simple to model that sort of complexity. They abstracted just one feature of real-world convection: the circular motion of hot fluid rising up and around like a Ferris wheel. The equations took into account the velocity of that motion and the transfer of heat. Those physical processes interacted. As any given bit of hot fluid rose around the circle, it would come into contact with cooler fluid and so begin to lose heat. If the circle was moving fast enough, the ball of fluid would not lose all its extra heat by the time it reached the top and started swinging down the other side of the roll, so it would actually begin to push back against the momentum of the other hot fluid coming up behind it.

Although the Lorenz system did not fully model convection, it did turn out to have exact analogues in real systems. For example, his equations precisely describe an old-fashioned electrical dynamo, the ancestor of modern generators, where current flows through a disc that rotates through a magnetic field. Under certain conditions the dynamo can reverse itself. And some scientists, after Lorenz’s equations became better known, suggested that the behavior of such a dynamo might provide an explanation for another peculiar reversing phenomenon: the earth’s magnetic field. The “geodynamo” is known to have flipped many times during the earth’s history, at intervals that seem erratic and inexplicable. Faced with such irregularity, theorists typically look for explanations outside the system, proposing such causes as meteorite strikes. Yet perhaps the geodynamo contains its own chaos.

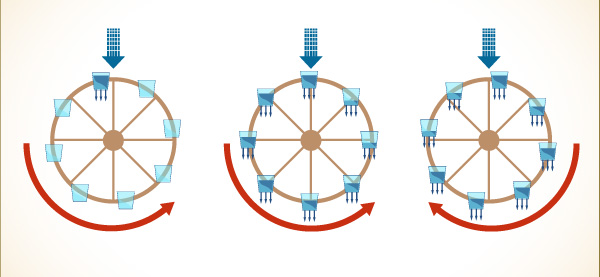
THE LORENZIAN WATERWHEEL. The first, famous chaotic system discovered by Edward Lorenz corresponds exactly to a mechanical device: a waterwheel. This simple device proves capable of surprisingly complicated behavior.

The rotation of the waterwheel shares some of the properties of the rotating cylinders of fluid in the process of convection. The waterwheel is like a slice through the cylinder. Both systems are driven steadily—by water or by heat—and both dissipate energy. The fluid loses heat; the buckets lose water. In both systems, the long-term behavior depends on how hard the driving energy is.

Water pours in from the top at a steady rate. If the flow of water in the waterwheel is slow, the top bucket never fills up enough to overcome friction, and the wheel never starts turning. (Similarly, in a fluid, if the heat is too low to overcome viscosity, it will not set the fluid in motion.)

If the flow is faster, the weight of the top bucket sets the wheel in motion (left). The waterwheel can settle into a rotation that continues at a steady rate (center).

But if the flow is faster still (right), the spin can become chaotic, because of nonlinear effects built into the system. As buckets pass under the flowing water, how much they fill depends on the speed of spin. If the wheel is spinning rapidly, the buckets have little time to fill up. (Similarly, fluid in a fast-turning convection roll has little time to absorb heat.) Also, if the wheel is spinning rapidly, buckets can start up the other side before they have time to empty. As a result, heavy buckets on the side moving upward can cause the spin to slow down and then reverse.

In fact, Lorenz discovered, over long periods, the spin can reverse itself many times, never settling down to a steady rate and never repeating itself in any predictable pattern.

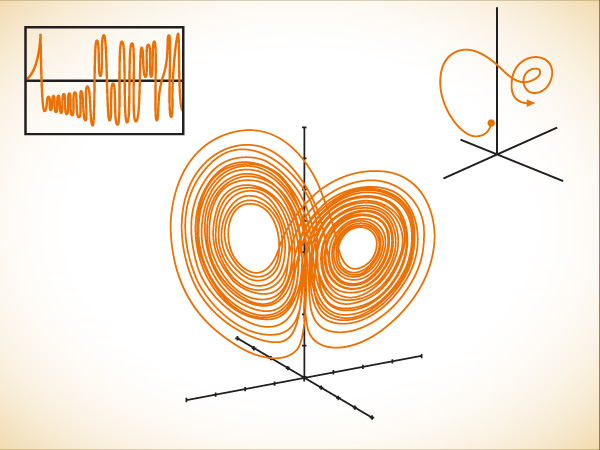
THE LORENZ ATTRACTOR (on facing page). This magical image, resembling an owl’s mask or butterfly’s wings, became an emblem for the early explorers of chaos. It revealed the fine structure hidden within a disorderly stream of data. Traditionally, the changing values of any one variable could be displayed in a so-called time series (top). To show the changing relationships among three variables required a different technique. At any instant in time, the three variables fix the location of a point in three-dimensional space; as the system changes, the motion of the point represents the continuously changing variables.

Because the system never exactly repeats itself, the trajectory never intersects itself. Instead it loops around and around forever. Motion on the attractor is abstract, but it conveys the flavor of the motion of the real system. For example, the crossover from one wing of the attractor to the other corresponds to a reversal in the direction of spin of the waterwheel or convecting fluid.

Another system precisely described by the Lorenz equations is a certain kind of water wheel, a mechanical analogue of the rotating circle of convection. At the top, water drips steadily into containers hanging on the wheel’s rim. Each container leaks steadily from a small hole. If the stream of water is slow, the top containers never fill fast enough to overcome friction, but if the stream is faster, the weight starts to turn the wheel. The rotation might become continuous. Or if the stream is so fast that the heavy containers swing all the way around the bottom and start up the other side, the wheel might then slow, stop, and reverse its rotation, turning first one way and then the other.

A physicist’s intuition about such a simple mechanical system—his pre-chaos intuition—tells him that over the long term, if the stream of water never varied, a steady state would evolve. Either the wheel would rotate steadily or it would oscillate steadily back and forth, turning first in one direction and then the other at constant intervals. Lorenz found otherwise.

Three equations, with three variables, completely described the motion of this system. Lorenz’s computer printed out the changing values of the three variables: 0-10-0; 4-12-0; 9-20-0; 16-36-2; 30-66-7; 54-115-24; 93-192-74. The three numbers rose and then fell as imaginary time intervals ticked by, five time steps, a hundred time steps, a thousand.

To make a picture from the data, Lorenz used each set of three numbers as coordinates to specify the location of a point in three-dimensional space. Thus the sequence of numbers produced a sequence of points tracing a continuous path, a record of the system’s behavior. Such a path might lead to one place and stop, meaning that the system had settled down to a steady state, where the variables for speed and temperature were no longer changing. Or the path might form a loop, going around and around, meaning that the system had settled into a pattern of behavior that would repeat itself periodically.

Lorenz’s system did neither. Instead, the map displayed a kind of infinite complexity. It always stayed within certain bounds, never running off the page but never repeating itself, either. It traced a strange, distinctive shape, a kind of double spiral in three dimensions, like a butterfly with its two wings. The shape signaled pure disorder, since no point or pattern of points ever recurred. Yet it also signaled a new kind of order.

YEARS LATER, PHYSICISTS would give wistful looks when they talked about Lorenz’s paper on those equations—“that beautiful marvel of a paper.” By then it was talked about as if it were an ancient scroll, preserving secrets of eternity. In the thousands of articles that made up the technical literature of chaos, few were cited more often than “Deterministic Nonperiodic Flow.” For years, no single object would inspire more illustrations, even motion pictures, than the mysterious curve depicted at the end, the double spiral that became known as the Lorenz attractor. For the first time, Lorenz’s pictures had shown what it meant to say, “This is complicated.” All the richness of chaos was there.

At the time, though, few could see it. Lorenz described it to Willem Malkus, a professor of applied mathematics at M.I.T., a gentlemanly scientist with a grand capacity for appreciating the work of colleagues. Malkus laughed and said, “Ed, we know—we know very well—that fluid convection doesn’t do that at all.” The complexity would surely be damped out, Malkus told him, and the system would settle down to steady, regular motion.

“Of course, we completely missed the point,” Malkus said a generation later—years after he had built a real Lorenzian waterwheel in his basement laboratory to show nonbelievers. “Ed wasn’t thinking in terms of our physics at all. He was thinking in terms of some sort of generalized or abstracted model which exhibited behavior that he intuitively felt was characteristic of some aspects of the external world. He couldn’t quite say that to us, though. It’s only after the fact that we perceived that he must have held those views.”

Few laymen realized how tightly compartmentalized the scientific community had become, a battleship with bulkheads sealed against leaks. Biologists had enough to read without keeping up with the mathematics literature—for that matter, molecular biologists had enough to read without keeping up with population biology. Physicists had better ways to spend their time than sifting through the meteorology journals. Some mathematicians would have been excited to see Lorenz’s discovery; within a decade, physicists, astronomers, and biologists were seeking something just like it, and sometimes rediscovering it for themselves. But Lorenz was a meteorologist, and no one thought to look for chaos on page 130 of volume 20 of the Journal of the Atmospheric Sciences.